Autoencoders: explicación y tutorial en Python
En este post veremos una completa explicación y un tutorial acerca de los Autoencoders, una importante arquitectura del Machine Learning que usa el aprendizaje no supervisado y que tiene aplicaciones en el procesamiento de imágenes y la detección de anomalías.
En el tutorial veremos cómo implementar un Autoencoder en Python, capaz de detectar transacciones fraudulentas en el uso de tarjetas débito o crédito.
Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
En posts anteriores hemos visto cómo usar las Redes Neuronales para clasificar imágenes donde, a través del entrenamiento, la red aprende a extraer la información relevante de estos datos para luego determinar a qué categoría pertenece cada uno de ellos.
En este post hablaremos de otra de las aplicaciones de las Redes Neuronales: los Autoencoders, que permiten obtener una representación compacta de los datos de entrada, y que se usan por ejemplo para detectar anomalías o para la eliminación de ruido o generación de imágenes, entre otras aplicaciones.
Además de analizar en detalle en qué consiste un Autoencoder, veremos una aplicación práctica. En el ejemplo que realizaremos veremos paso a paso cómo implementar un Autoencoder usando Python y la librería Keras para detectar fraudes en transacciones hechas con tarjetas debito o crédito.
Principio de funcionamiento de las Redes Neuronales
Las Redes Neuronales que hemos visto en posts anteriores son capaces de tomar datos relativamente complejos (imágenes, sonidos, videos, etc.) y de clasificarlos, determinando así si el dato pertenece a una de varias posibles categorías:
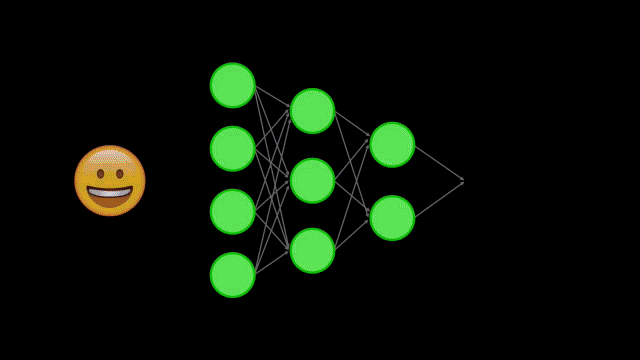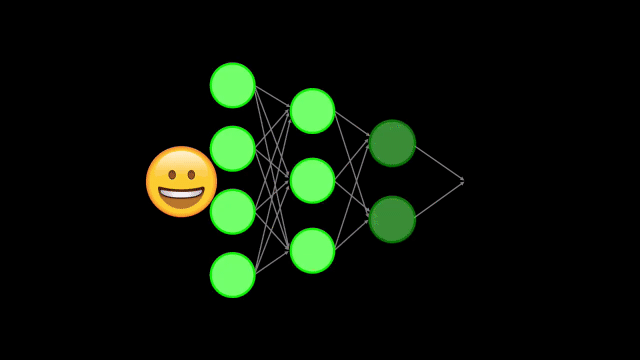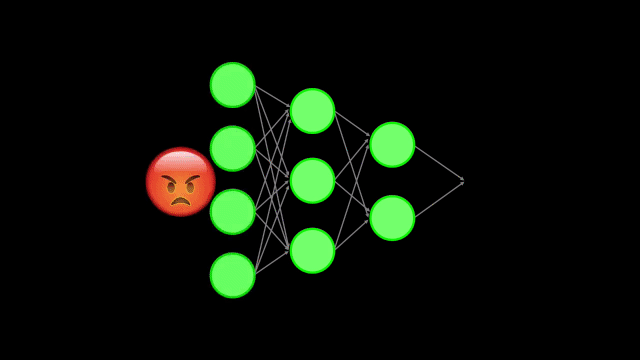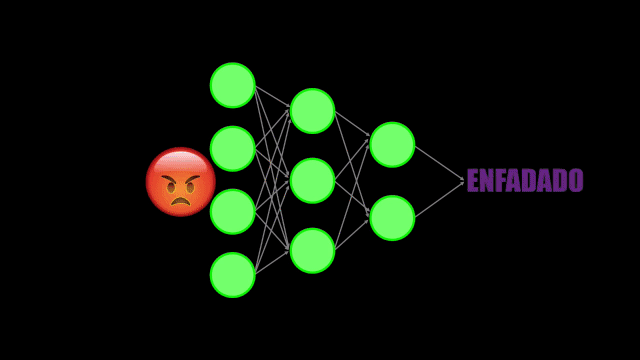
Para lograr esto la Red Neuronal se entrena con una cantidad considerable de datos, y durante este proceso aprende a extraer la información o características más relevantes de esos datos de entrenamiento.
Este proceso se conoce como extracción de características, y permite representar la entrada a la Red Neuronal de una forma más compacta, reduciendo así la dimensionalidad de los datos de entrada:
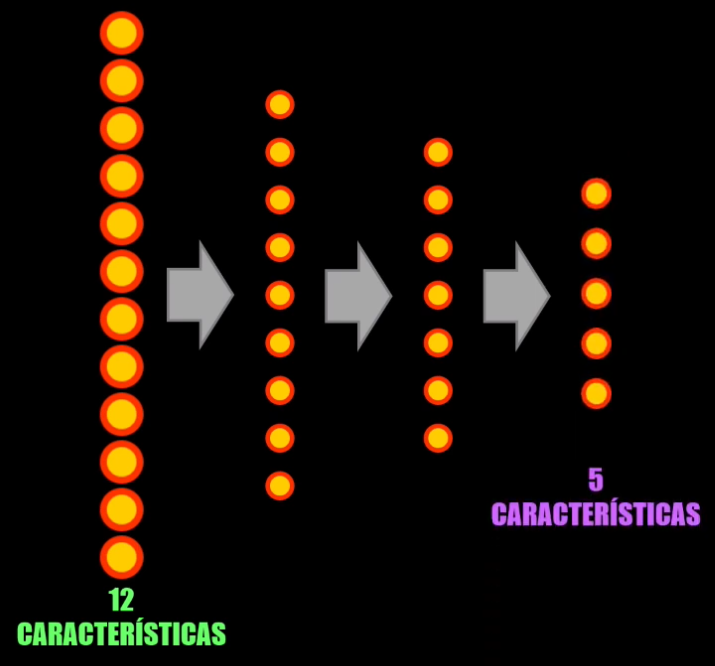
¿Qué es un Autoencoder?
Una idea general
¿Qué pasa si en lugar de clasificar el dato de entrada intentamos reconstruirlo?
Es decir, ¿qué pasa si entrenamos la Red Neuronal para que aprenda a generar a la salida el mismo dato de entrada?
¡En este caso tendremos precisamente un Autoencoder!
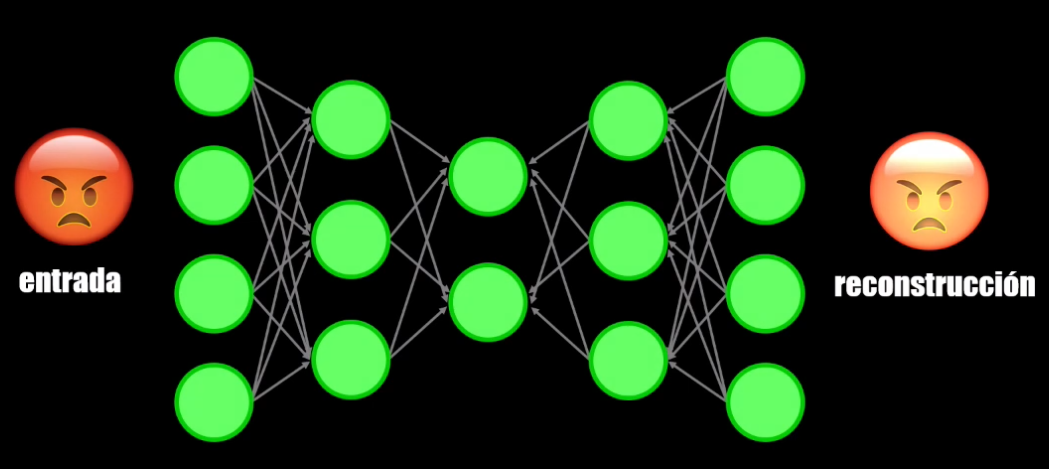
Elementos del Autoencoder
Un Autoencoder tiene tres elementos:
- Un encoder que permite comprimir el dato de entrada:
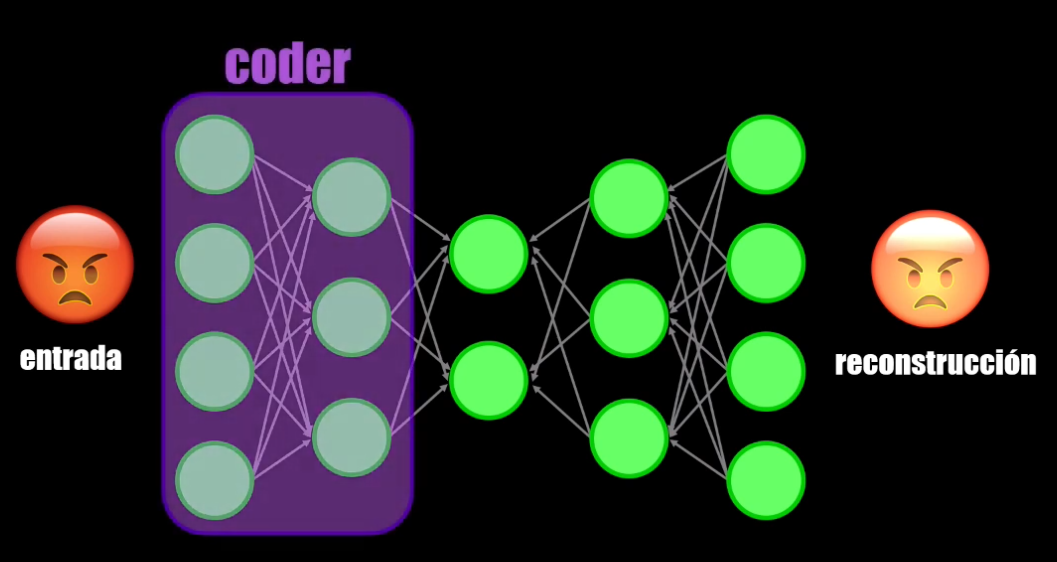
- El bottleneck (o cuello de botella, resultado de la compresión) que es como tal la representación compacta obtenida:
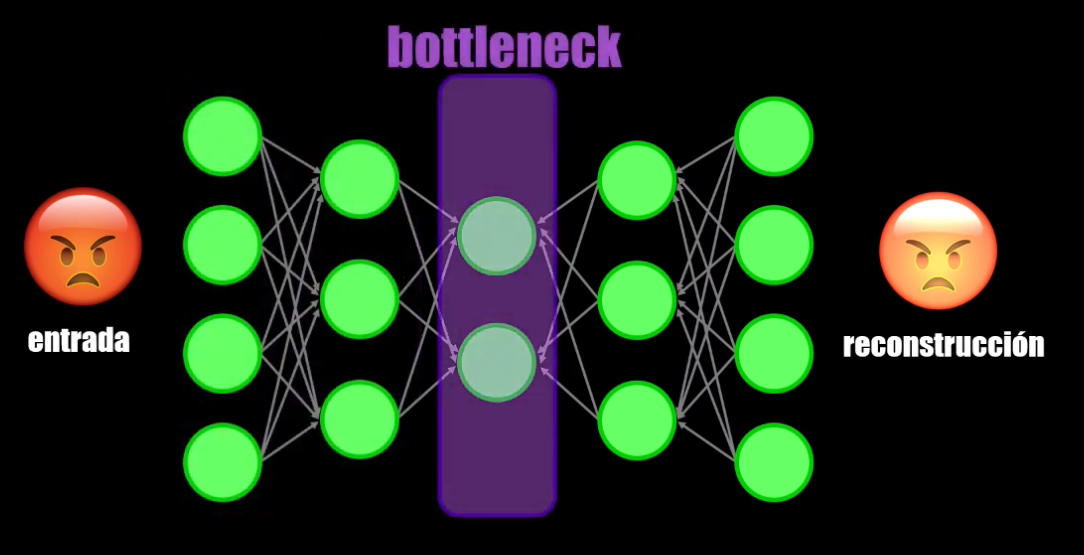
- Y el decoder, que reconstruye la entrada a partir del bottleneck:
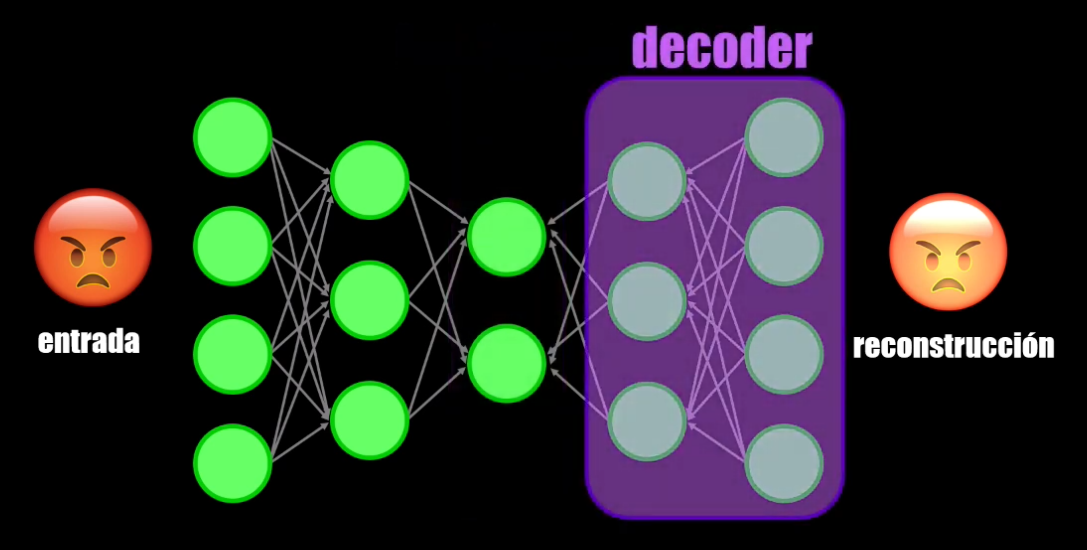
¿Pero para qué queremos entrenar una Red Neuronal que sea capaz de generar el mismo dato de entrada?
El bottleneck: una forma de comprimir el dato
Si observamos el bottleneck veremos que en este punto del Autoencoder se tiene una representación compacta de la entrada. Es decir, que el dato obtenido es una versión comprimida de la entrada, y que por tanto contiene una menor cantidad de datos.
La representación obtenida en el bottleneck se conoce como espacio latente y es el resultado del entrenamiento, en donde la red aprende a extraer la información más relevante del dato de entrada:
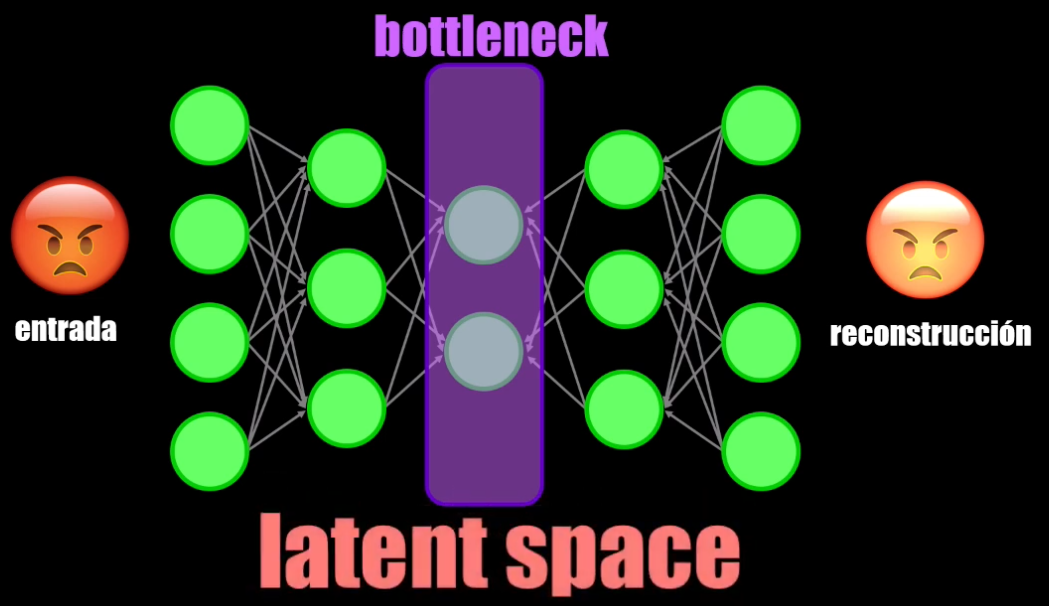
Entrenamiento del Autoencoder
Para lograr encontrar esta representación compacta, el Autoencoder es entrenado de manera similar a una Red Neuronal.
Sin embargo, en este caso la función de error usada para actualizar los coeficientes del autoencoder es simplemente el resultado de comparar, punto a punto, el dato reconstruido con el dato original:
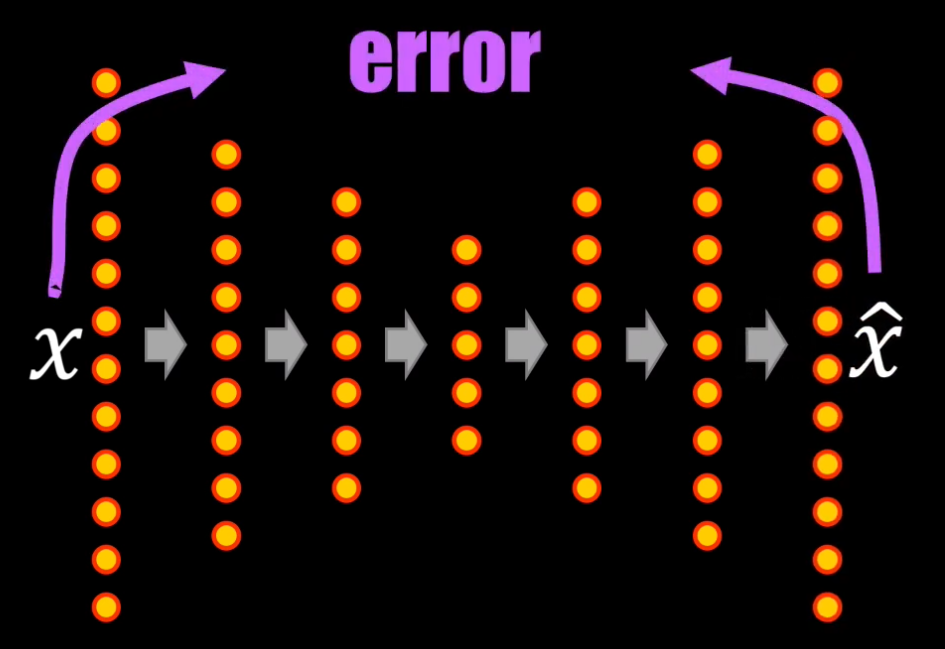
Teniendo esto en cuenta podemos decir que el Autoencoder es un ejemplo de aprendizaje no supervisado, pues realmente durante el entrenamiento no definimos la categoría a la que pertenece cada entrada, ¡pues lo que queremos es que la salida sea precisamente el mismo dato de entrada!
Algunas aplicaciones de los Autoencoders
La representación compacta obtenida con el Autoencoder es útil por ejemplo para eliminar ruido en imágenes o para detectar anomalías en una serie de datos:
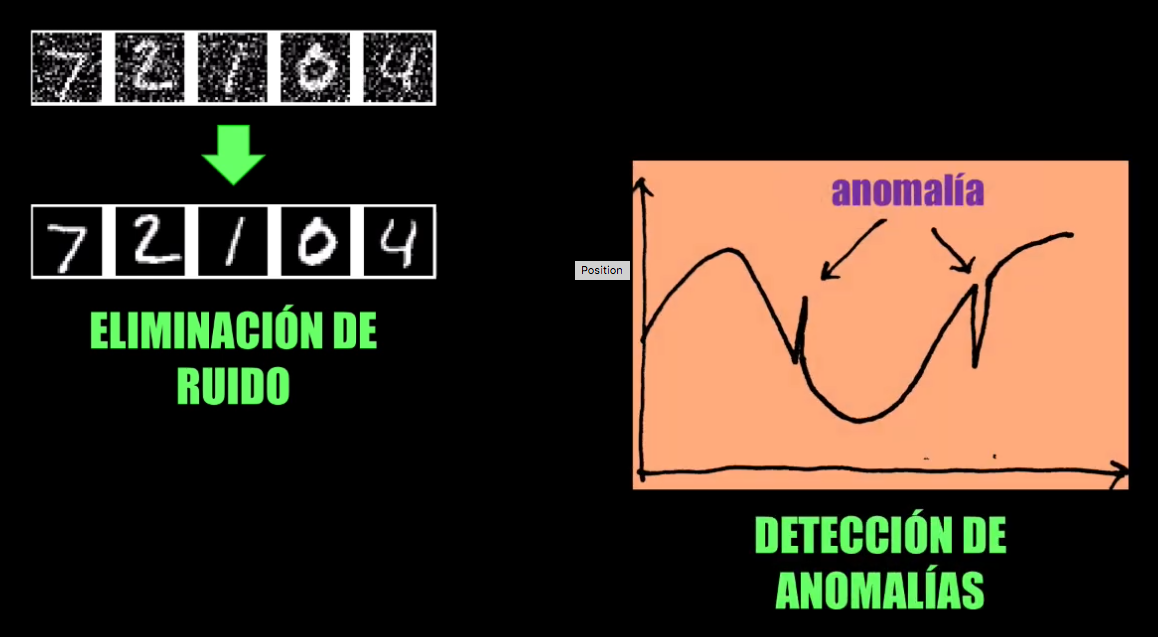
Es precisamente en la detección de anomalías en donde se centra el tutorial que veremos a continuación.
Tutorial: detección de fraudes usando Autoencoders
El problema a resolver
A nivel mundial, y durante el año 2015, el fraude por uso de tarjetas (débito o crédito) fue de 22 billones de dólares, y se espera que para el año 2020 este monto ascienda a 32 billones.
Varias empresas del sector han venido usando técnicas de Machine Learnin, como las Máquinas de Soporte Vectorial y técnicas de clustering, para detectar estos fraudes, pero sin resultados exitosos.
Recientemente, empresas como PayPal, han comenzado a hacer uso de técnicas de “Deep Learning” y autoencoders para la detección de fraudes.
Para implementar el autoencoder de este ejemplo usaremos un set de datos que contiene registros de transacciones realizadas en Europa durante septiembre de 2013. La idea es determinar cuáles de estos registros corresponden a transacciones fraudulentas, para lo cual diseñaremos un Autoencoder.
Este tutorial está implementado en Python, y se divide en cinco partes: primero realizaremos la lectura y análisis exploratorio del set de datos. En segundo lugar realizaremos el pre-procesamiento de los datos. Luego implementaremos el autoencoder y haremos su entrenamiento con ayuda de la librería Keras, y finalmente lo usaremos para detectar posibles transacciones fraudulentas en nuestro set de datos.
Comencemos entonces con la lectura y pre-procesamiento de los datos.
1. Lectura y análisis exploratorio de los datos
El set de datos contiene en total 284.315 transacciones “normales” y tan solo 492 “fraudulentas”. Para realizar la lectura usaremos la librería Pandas de Python:
import pandas as pd
datos = pd.read_csv("creditcard.csv")
print(datos.head())
nr_clases = datos['Class'].value_counts(sort=True)
La variable nr_clases contiene precisamente las transacciones normales y las fraudulentas.
Cada uno de estos datos contiene 30 características. Por motivos de confidencialidad, el proveedor del set de datos ha transformado las características V1 a V28 usando PCA (principal component analysis, una técnica usada para reducir la redundancia de información). Las características 29 y 30 (“Time” y “Amount”) indican la cantidad de segundos transcurridos desde el primer registro del dataset así como el monto (en euros) de la transacción:
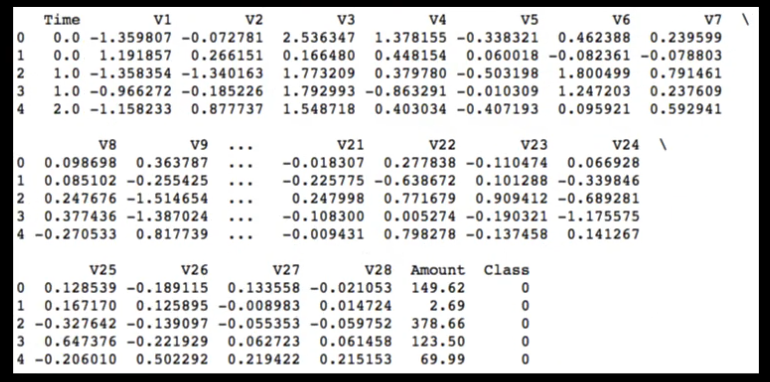
Hagamos una exploración preliminar de los datos. Con ello podremos verificar que no hay una forma simple de detectar los fraudes, lo que justificará el uso de un Autoencoder.
En primer lugar podemos obtener una gráfica que muestre la distribución de los registros “normales” y “fraudulentos”:
nr_clases.plot(kind = 'bar', rot=0)
plt.xticks(range(2), ['Normales', 'Fraudulentos'])
plt.title("Distribución de los datos")
plt.xlabel("Clase")
plt.ylabel("Cantidad")
plt.show()
Podemos ver que los datos no están para nada balanceados, y la gran mayoría corresponde a registros “normales”:
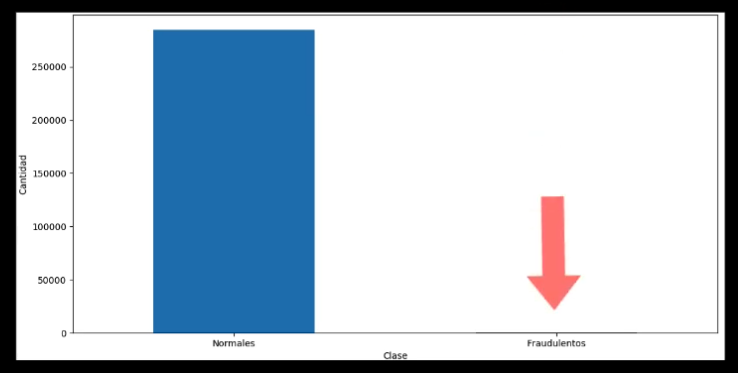
Veamos ahora cómo se comportan los dos tipos de dato con respecto al tiempo:
normales = datos[datos.Class==0]
fraudulentos = datos[datos.Class==1]
plt.scatter(normales.Time/3600, normales.Amount,
alpha = 0.5, c='#19323C', label='Normales', s=3)
plt.scatter(fraudulentos.Time/3600, fraudulentos.Amount,
alpha = 0.5, c='#F2545B', label='Fraudulentos', s=3)
plt.xlabel('Tiempo desde la primera transacción (h)')
plt.ylabel('Monto (Euros)')
plt.legend(loc='upper right')
plt.show()
Observamos que no hay un patrón en particular, y que las transacciones “normales” y las “fraudulentas” no pueden ser discriminadas usando la variable tiempo:
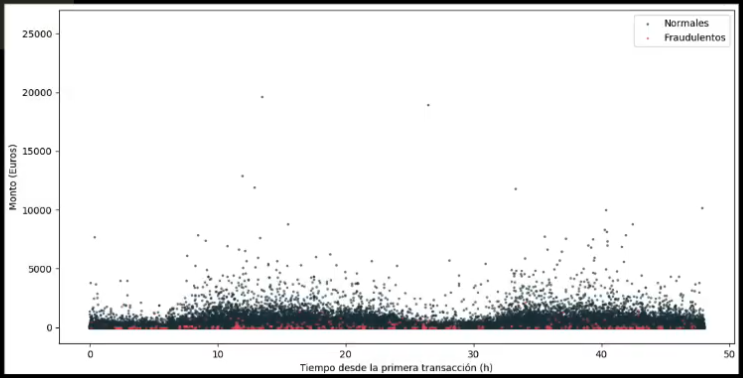
¿Es posible que el monto de cada transacción nos permita diferenciar un tipo de dato de otro?:
import numpy as np
bins = np.linspace(200, 2500, 100)
plt.hist(normales.Amount, bins, alpha=1, normed=True,
label='Normales', color='#19323C')
plt.hist(fraudulentos.Amount, bins, alpha=0.6,
normed=True, label='Fraudulentos', color='#F2545B')
plt.legend(loc='upper right')
plt.xlabel("Monto de la transacción (Euros)")
plt.ylabel("Porcentaje de las transacciones (%)")
plt.show()
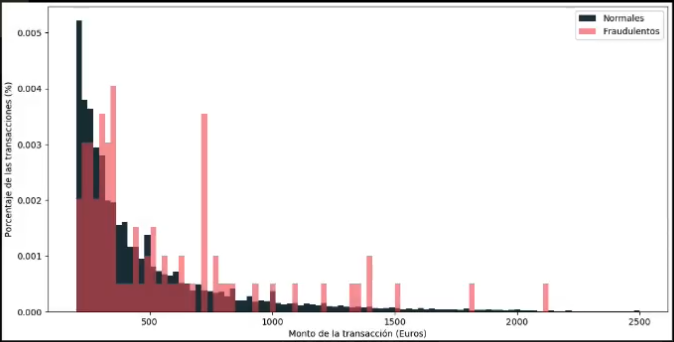
Al observar la distribución de transacciones con respecto al monto, vemos que tampoco hay una clara diferencia, pues a pesar de que los registros “fraudulentos” tienden a tener montos más bajos, de todos modos estos se solapan con la distribución de los registros “normales”.
Por último, veamos si las distribuciones de características V1 a V28 presentan alguna diferencia entre los dos tipos de registros:
import matplotlib.gridspec as gridspec
import seaborn as sns
v_1_28 = datos.iloc[:,1:29].columns
gs = gridspec.GridSpec(28, 1)
for i, cn in enumerate(datos[v_1_28]):
sns.distplot(datos[cn][datos.Class == 1], bins=50,
label='Fraudulentos', color='#F2545B')
sns.distplot(datos[cn][datos.Class == 0], bins=50,
label='Normales', color='#19323C')
plt.xlabel('')
plt.title('Histograma característica: ' + str(cn))
plt.legend(loc='upper right')
plt.show()
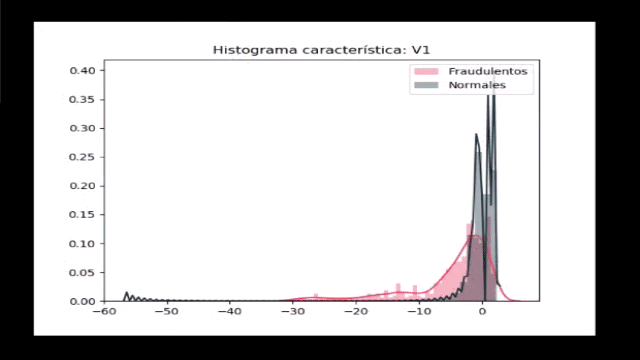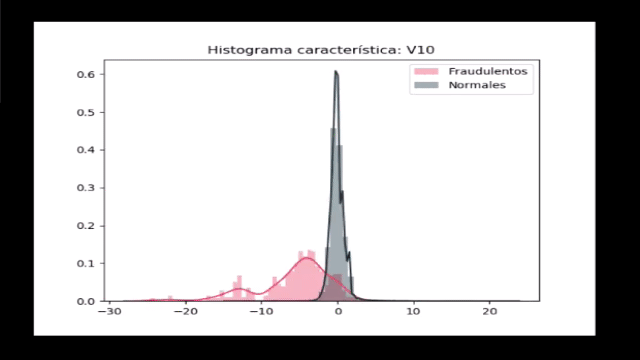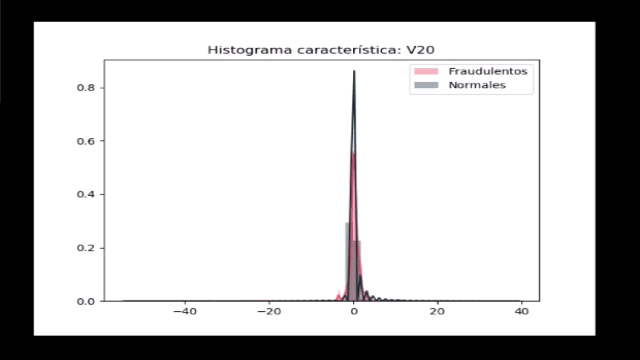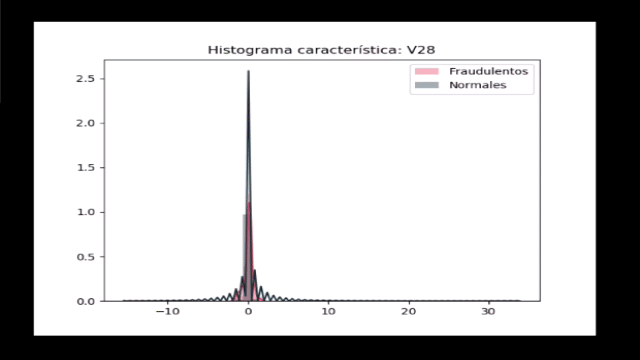
Observamos que ninguna de estas características permite una clara diferenciación de los datos, y con esto concluimos que un método simple (enfocado por ejemplo en definir un umbral que permita separar unas características de otras) no resulta útil.
Con este análisis preliminar podemos concluir que no existe una forma sencilla de separar una categoría de la otra, y que tampoco podemos entrenar una Red Neuronal para realizar esta clasificación pues el set de datos está desbalanceado: existen muchos más registros “normales” que “fraudulentos”.
Lo anterior justifica el uso de un Autoencoder. Sin embargo, primero veamos cómo realizar el pre-procesamiento de los datos.
2. Pre-procesamiento de los datos
Comencemos eliminando la característica “tiempo” del set de datos (pues, como vimos anteriormente, no brinda información relevante):
from sklearn.preprocessing import StandardScaler
datos.drop(['Time'], axis=1, inplace=True)
Además, normalicemos la característica “amount” (el monto de las transacciones), para que tenga valor medio igual a cero y desviación estándar igual a 1 (comparables con las características V1 a V28). Esto garantizará la convergencia del algoritmo del Gradiente Descendente durante el entrenamiento:
datos['Amount'] = StandardScaler().fit_transform(datos['Amount'].values.reshape(-1,1))
Ahora creemos el set de entrenamiento (que corresponde al 80% de los registros) y el de validación (que tendrá el 20% restante). Esto se logra fácilmente con la función train_test_split de la librería Scikit-Learn.
El autoencoder será entrenado únicamente con registros “normales”, para que de esta forma aprenda a obtener una representación compacta de esos datos “normales”. Una vez entrenado, y cuando se introduzca un registro “fraudulento”, se esperaría que la reconstrucción del dato no sea tan precisa y por tanto la diferencia (o error) entre el dato reconstruido y el original será más grande que aquella obtenida cuando el dato ingresado es normal.
Así que el set de entrenamiento contendrá únicamente registros normales, mientras que el de validación tendrá los dos tipos de registros (normales y fraudulentos):
from sklearn.model_selection import train_test_split
X_train, X_test = train_test_split(datos, test_size=0.2, random_state=42)
X_train = X_train[X_train.Class == 0] ## Usaremos únicamente la clase 0 (transacciones normales)
X_train = X_train.drop(['Class'], axis=1)
X_train = X_train.values
Y_test = X_test['Class']
X_test = X_test.drop(['Class'], axis=1)
X_test = X_test.values
Perfecto. Tenemos listos nuestros sets de entrenamiento y validación. Veamos ahora cómo implementar el Autoencoder en Keras.
3. Creación del Autoencoder en Keras
Diseñaremos un autoencoder con las siguientes características:
- 29 entradas, correspondientes al número de características de cada dato de entrenamiento,
- El encoder, encargado de obtener una representación compacta de la entrada, tendrá una primera capa con 20 neuronas, con función de activación tanh seguida de otra capa con 14 neuronas y activación ReLU. Esto quiere decir que el dato comprimido tendrá un tamaño igual a 14.
- El decoder, encargado de reconstruir el dato original a partir de su versión comprimida, tendrá una capa con 20 neuronas y activación tanh seguida por la capa de salida con 29 neuronas y activación ReLU, cuya salida corresponde a la versión reconstruida.
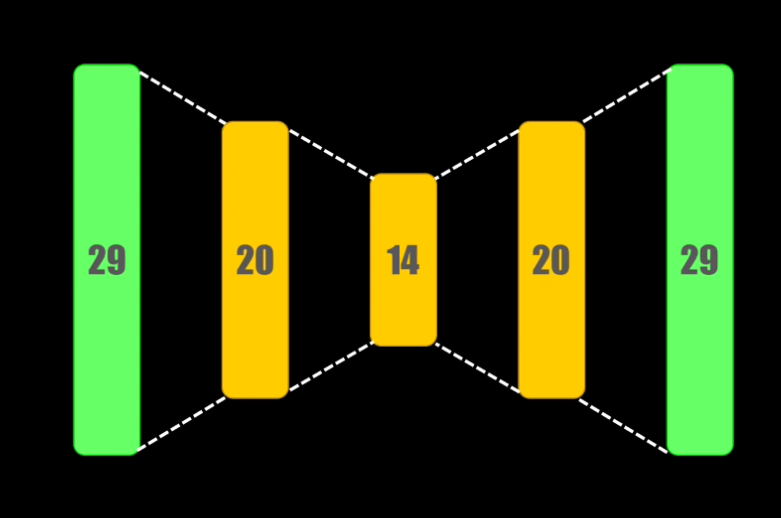
Para crear este Autoencoder primero definimos la capa de entrada, que tendrá el mismo número de elementos que cada ejemplo en el set de entrenamiento (es decir 29 datos):
import numpy as np
np.random.seed(5)
from keras.layers import Input
dim_entrada = X_train.shape[1]
capa_entrada = Input(shape=(dim_entrada,))
En donde en las líneas de código anteriores hemos usado np.random.seed(5) para fijar la semilla del generatorio aleatorio y garantizar de esta forma la reproducibilidad del algoritmo.
A continuación creamos el encoder con dos capas, de 20 y 14 neuronas, y funciones de activación tanh y relu respectivamente:
from keras.layers import Dense
encoder = Dense(20, activation='tanh')(capa_entrada)
encoder = Dense(14, activation='relu')(encoder)
El encoder que acabamos de crear permite pasar de un dato de entrada con 29 características a una representación compacta con 14 características.
Ahora implementaremos el decoder, que realiza el proceso de reconstrucción del dato, pasando de una representación compacta con 14 características a la versión reconstruida con 29 características.
El decoder tendrá entonces dos capas: la primera con 20 y la segunda con 29 neuronas. Acá usamos nuevamente las funciones de activación tanh y relu:
decoder = Dense(20, activation='tanh')(encoder)
decoder = Dense(29, activation='relu')(decoder)
Finalmente, combinamos la capa de entrada, el encoder y el decoder en un modelo de Keras, que será precisamente el autoencoder. Esto lo hacemos con la función Model, donde basta únicamente con especificar la capa de entrada y el decoder, y Keras automáticamente se encarga de interconectar todos los objetos:
from keras.models import Model
autoencoder = Model(inputs=capa_entrada, outputs=decoder)
Ahora debemos compilar el modelo. Es decir que debemos definir el algoritmo para minimizar la función de error, que será el Gradiente Descendente (SGD en Keras). Este método usará una tasa de aprendizaje de 0.01.
También debemos definir la función de error, que en este caso será el error cuadrático medio, que permitirá comparar punto a punto el dato de salida reconstruido con el dato original. En keras esta función se especifica con el parámetro loss='mse'.
Finalmente, todos estos parámetros se definen a través de la función compile:
from keras.optimizers import SGD
sgd = SGD(lr=0.01)
autoencoder.compile(optimizer='sgd', loss='mse')
4. Entrenamiento del Autoencoder
Recordemos que el entrenamiento se hará únicamente con las transacciones normales (set X_train).
Entrenaremos el modelo usando un total de 100 iteraciones, y usando tamaños de lote de 32 (es decir, presentaremos al modelo bloques de 32 ejemplos durante el entrenamiento).
Es importante observar que para este entrenamiento definimos X_train como el dato tanto de entrada como de salida del modelo:
nits = 100
tam_lote = 32
autoencoder.fit(X_train, X_train, epochs=nits, batch_size=tam_lote, shuffle=True, validation_data=(X_test,X_test), verbose=1)
5. Validación del modelo y detección de fraudes
Como el modelo fue entrenado sólo con transacciones normales, es de esperar que al introducir un registro fraudulento la reconstrucción del dato no sea tan precisa y por tanto la diferencia entre el dato reconstruido y el original será más grande que la obtenida cuando el dato ingresado es normal:
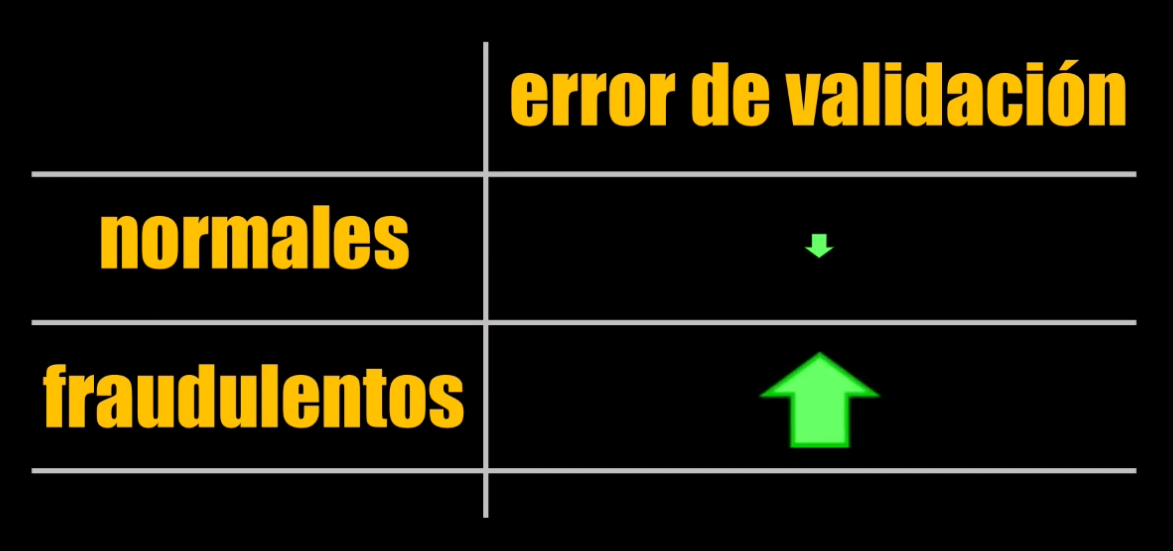
Así que para realizar la detección de fraudes seguiremos este procedimiento:
- En primer lugar tomaremos el Autoencoder entrenado y lo usaremos para generar una predicción, usando el set de validación (
X_test) - Luego calcularemos el error cuadrático medio entre el dato original (a la entrada del Autoencoder) y el dato reconstruido (generado a través de la predicción)
- Posteriormente estableceremos un umbral: si el error calculado en el punto anterior supera el umbral, tendremos un registro “fraudulento”, y en caso contrario tendremos un registro “normal”.
Esta idea del umbral debería funcionar, pues se espera que los registros “normales” tengan un error en la reconstrucción menor que los registros “fraudulentos”.
Veamos en detalle cada uno de estos pasos:
- Predicción: para generar la predicción usaremos la función
predict, que permitirá obtener la reconstrucción de cada dato de entrada:
X_pred = autoencoder.predict(X_test)
Cada uno de los datos predichos por el modelo tiene un total de 29 características (el mismo tamaño del dato de entrada).
- Cálculo del error cuadrático medio
ecm = np.mean(np.power(X_test-X_pred,2), axis=1)
- Definición del umbral:
Para definir el umbral, usaremos dos métricas que resultan útiles en casos como este (donde los datos no están balanceados): “precisión” y “recall”
Para esto tengamos en cuenta que el modelo puede generar cuatro tipos de clasificación:
- La situación ideal: un fraude es clasificado como un fraude. Esto se conoce como un “true positive” (ó TP, un positivo verdadero)
- Un fraude es clasificado como un registro normal. Esto se conoce como un “false negative” (FN ó un falso negativo)
- Un registro normal es clasificado como normal. Esto se conoce como un “true negative” (TN ó un verdadero negativo)
- Finalmente, un registro normal puede ser clasificado como fraudulento. Esto se conoce como “false positive” (FP ó un falso positivo).
Un clasificador ideal no debería generar ni falsos positivos ni falsos negativos. Sin embargo, ningún clasificador es ideal y por tanto siempre tendremos, en mayor o menor grado, falsos positivos y negativos.
El parámetro “precision” es una medida de la cantidad de falsos positivos generados por el clasificador. Si la cantidad de falsos positivos se reduce a cero, se alcanzaría una “precisión” máxima igual a 1.
Por su parte, el “recall” es una medida de la cantidad de falsos negativos generados por el clasificador. Si la cantidad de falsos negativos (FN) se reduce a cero, se alcanzaría un “recall” ideal igual a 1.

En la práctica no se pueden lograr simultáneamente los dos valores ideales: una mayor “precisión” implica sacrificar el “recall” y viceversa.
En nuestro Autoencoder, el precisión y el recall cambiarán dependiendo del umbral escogido. Para observar este comportamiento podemos hacer una gráfica del precisión y el recall vs el umbral, que en Scikit-Learn se puede obtener fácilmente usando la función precision_recall_curve:
from sklearn.metrics import precision_recall_curve
precision, recall, umbral = precision_recall_curve(Y_test, ecm)
plt.plot(umbral, precision[1:], label="Precision",linewidth=5)
plt.plot(umbral, recall[1:], label="Recall",linewidth=5)
plt.title('Precision y Recall para diferentes umbrales')
plt.xlabel('Umbral')
plt.ylabel('Precision/Recall')
plt.legend()
plt.show()
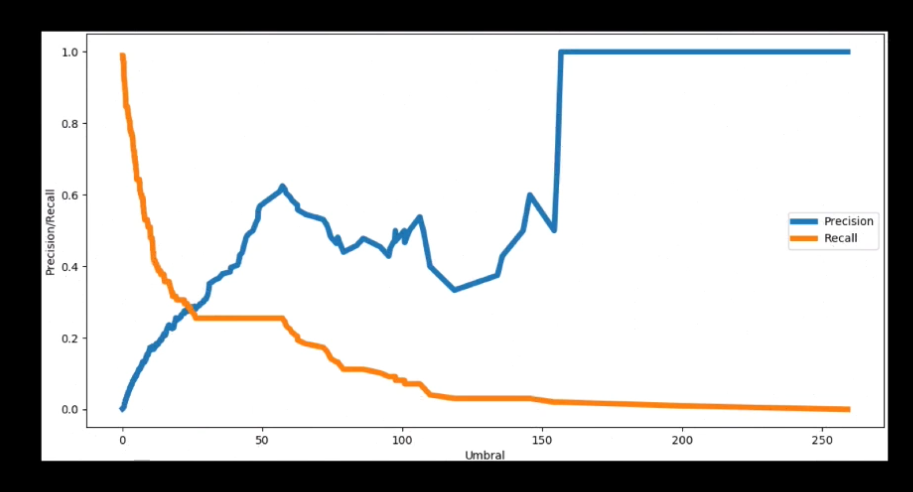
Como se mencionó anteriormente, en efecto el precisión y el recall tienen comportamientos opuestos: un aumento del umbral genera un aumento de la precisión pero una reducción en el recall.
Lo que queda ahora es definir el umbral, y esto depende de qué es lo que queremos favorecer. ¿Nos interesa detectar la mayor parte de los fraudes, es decir tener pocos falsos negativos, a costa de un alto número de falsos positivos? O por el contrario, ¿nos interesa que los registros normales sean clasificados correctamente, a costa de un elevado número de registros fraudulentos clasificados incorrectamente?
Para este ejemplo vamos a escoger la primera opción, es decir que ajustaremos el umbral para obtener un recall alto.
Fijaremos entonces un umbral de 0.75. Si el error de la predicción sobrepasa este umbral, asignaremos la categoría “0” (registro fraudulento), mientras que si el error es menor o igual al umbral asignaremos la categoría “1” (registro normal):
umbral_fijo = 0.75
Y_pred = [1 if e > umbral_fijo else 0 for e in ecm]
Finalmente, podemos imprimir la matriz de confusión de este clasificador tomando como referencia la categoría a la que corresponde realmente el dato (almacenada en la variable Y_test):
from sklearn.metrics import confusion_matrix
conf_matrix = confusion_matrix(Y_test, Y_pred)
print(conf_matrix)
Tengamos en cuenta que la matriz de confusión muestra en su diagonal principal el número de verdaderos negativos (normales clasificados como normales) y verdaderos positivos (fraudulentos clasificados como fraudulentos), mientras que en la diagonal secundaria encontraremos los falsos positivos (normales clasificados como fraudulentos) y los falsos negativos (fraudulentos clasificados como normales):
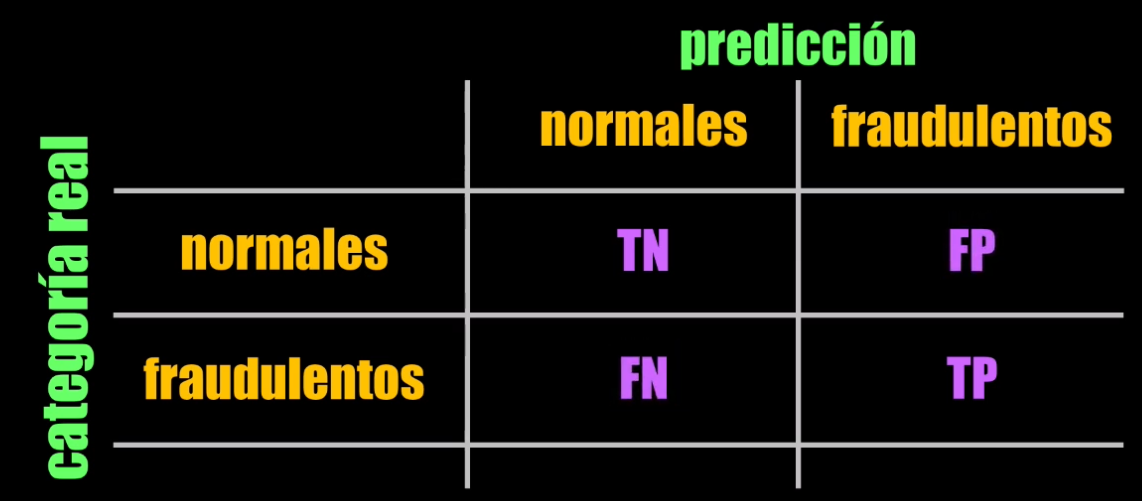
Al ejecutar el código anterior, obtenemos la siguiente matriz de confusión:
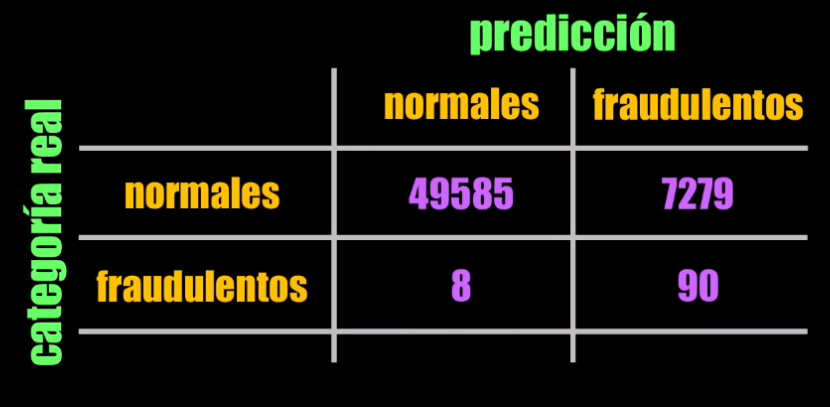
Con los datos de la matriz de confusión podemos obtener el precisión y recall logrados por el autoencoder con el umbral escogido.
Al momento de definir el umbral decidimos favorecer el recall, sacrificando el “precisión. De hecho, al observar la matriz de confusión vemos que 49580 datos normales fueron clasificados correctamente, mientras que 7284 fueron clasificados como fraudulentos. Es decir, tenemos una cantidad relativamente alta de falsos positivos, y por tanto un “precision” de tan solo 0.01!
Sin embargo, al analizar el recall, vemos que un total de 90 registros fraudulentos fueron detectados correctamente, mientras que 8 de ellos fueron detectados como registros normales. ¡No está nada mal!, pues tenemos un recall de 0.92.
Con esto podemos concluir que para el Autoencoder diseñado, y con el umbral seleccionado, se tiene un buen desempeño al momento de detectar registros fraudulentos.
Datos y código fuente
En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.
Conclusión
Bien, en este post hemos visto una explicación detallada del Autoencoder, una variante de las Redes Neuronales que permite encontrar una representación compacta de los datos de entrada.
Este principio de funcionamiento lo aprovechamos en el tutorial, en donde implementamos en Python un Autoencoder capaz de detectar operaciones fraudulentas en el uso de tarjetas, con un recall bastante alto ( igual a 0.92).
Es posible aún refinar este modelo, probando variantes del autoenconder (agregando o quitando capas o cambiando el número de neuronas en cada capa) o modificando el umbral, para tratar de lograr un recall aún más alto que el que obtuve en este tutorial.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: