La Función de Activación
En este post hablaremos de un elemento fundamental de cualquier tipo de Red Neuronal: la Función de Activación. Veremos las diferentes funciones de activación usadas en las Redes Neuronales, así como las ventajas y desventajas de cada una de ellas.
Al final de esta entrada habremos visto:
- La importancia de usar las funciones de activación
- Las funciones de activación más usadas en la implementación de Redes Neuronales
- Los pros y contras de cada una de estas funciones
- Algunas recomendaciones de uso
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
Anteriormente vimos cómo las Redes Neuronales son capaces de aproximar cualquier función matemática. Esta versatilidad se debe, en buena parte, al uso de diversas funciones de activación.
Recordemos que la Neurona Artificial es el elemento esencial de cualquier Red Neuronal. Al combinar múltiples neuronas de forma adecuada, podemos obtener una Red Neuronal con la capacidad de realizar procesos de regresión y de clasificación bastante complejos.
Esta versatilidad se debe en gran parte al uso de una Función de Activación en cada una de las neuronas de la red. Sin embargo, es importante recordar que esta función debe satisfacer una característica esencial: su comportamiento debe ser no lineal.
A continuación veremos en detalle las principales funciones de activación usadas en las todos los tipos de redes neuronales, desde las convencionales Redes Neuronales y Convolucionales, hasta las Redes Recurrentes, las Redes LSTM y las Redes Transformer. Discutiremos además sus principales características, ventajas y desventajas en términos de la implementación de estos modelos.
Las funciones de activación más usadas en Deep Learning
La función sigmoidal (σ)
Esta función de activación toma cualquier rango de valores a la entrada y los mapea al rango de 0 a 1 a la salida. Dicho comportamiento se muestra en la siguiente figura:
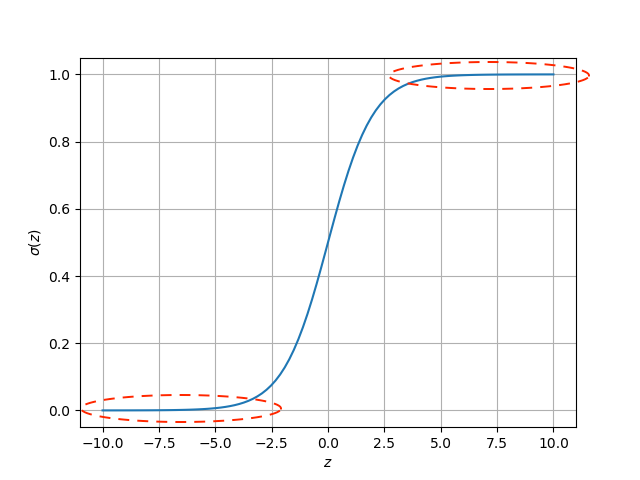
En la actualidad esta función de activación tiene un uso limitado, y realmente su principal aplicación es la clasificación binaria.
Lo anterior se debe al problema de saturación. Como se observa en la figura anterior, la función se satura a 1 cuando la entrada (z) es muy alta, y a 0 cuando es muy baja. Esto hace que durante el entrenamiento usando el método del gradiente descendente, los gradientes calculados sean muy pequeños, dificultando así la convergencia del algoritmo.
La función tangente hiperbólica (tanh)
Esta función tiene un comportamiento muy similar a la sigmoidal, con la diferencia de que los valores de salida estarán en el rango de -1 a 1:
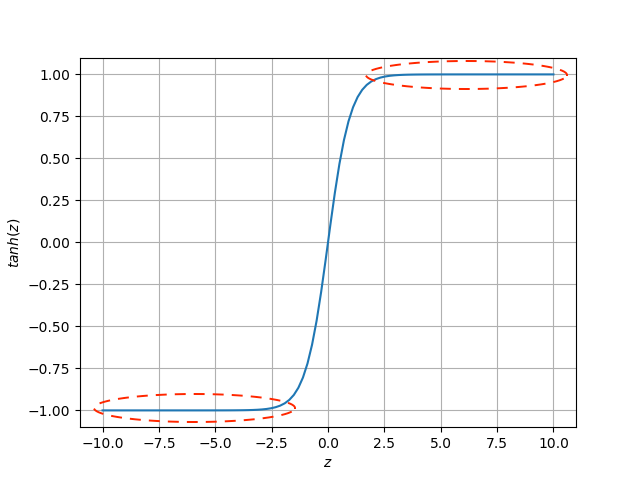
En este caso, la función también sufre del problema de saturación, pero ofrece la ventaja de tener una salida simétrica lo cual facilita el proceso de entrenamiento.
A pesar de lo anterior es evidente que el problema de la saturación también limita la aplicabilidad de esta función de activación en Redes Neuronales.
La función ReLU, que veremos a continuación, resuelve precisamente este inconveniente.
La función ReLU
Su nombre viene de las siglas en Inglés de Rectified Linear Unit (o unidad lineal rectificada). El comportamiento de esta función se muestra en la siguiente figura:
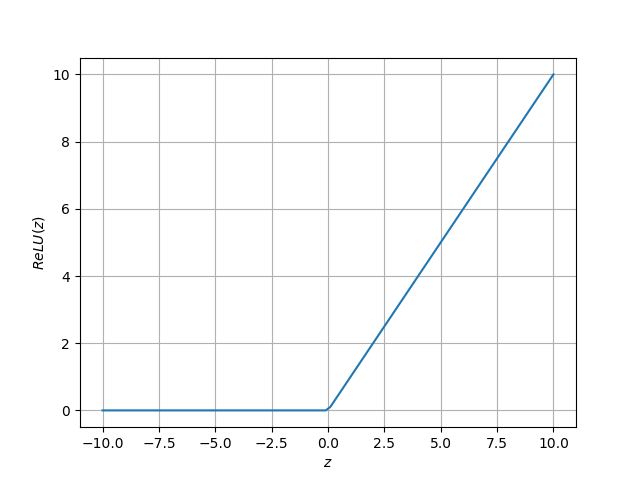
Esta función generará una salida igual a cero cuando la entrada (z) sea negativa, y una salida igual a la entrada cuando dicha esta última sea positiva.
La función de activación ReLU se ha convertido en la más usada en los modelos Deep Learning durante los últimos años, lo cual se debe principalmente a:
- La no existencia de saturación, como sí ocurre en las funciones sigmoidal y tanh. Lo anterior hace que el algoritmo del gradiente descendente converja mucho más rápidamente, facilitando así el entrenamiento.
- Es más fácil de implementar computacionalmente en comparación con las otras dos funciones, que requieren el cálculo de funciones matemáticas más complejas como la exponencial.
Habiendo visto las principales características de cada función de activación, veamos finalmente algunas recomendaciones de uso al implementar Redes Neuronales.
La función de activación: recomendaciones de uso
La primera recomendación es usar siempre la función ReLU en las capas ocultas de la Red Neuronal. Lo anterior hace que el entrenamiento sea más rápido y es mucho más probable que logre la convergencia del algoritmo del gradiente descendente.
En segundo lugar, se recomienda el uso de las funciones sigmoidal o tanh únicamente para las capas de salida, por ejemplo en la implementación de un clasificador binario.
Conclusión
Antes de finalizar, resumamos las ideas más importantes con relación a la función de activación:
- La función de activación debe ser no lineal.
- Las funciones sigmoidal, tanh y ReLU son las más usadas convencionalmente en modelos Deep Learning.
- El principal inconveniente de las funciones sigmoidal y tanh es la saturación de sus valores de salida. Esto dificulta el proceso de entrenamiento al no permitir la rápida minimización de la función de error usando el método del Gradiente Descendente
- Por lo anterior se sugiere usar las funciones sigmoidal y tanh únicamente en las capas de salida, para tareas de clasificación binaria.
- ReLU es la función de activación más usada en la actualidad, pues no tiene problemas de saturación y es más fácil de implementar que las funciones sigmoidal y tanh.
- Se recomienda el uso de la función ReLU en las capas ocultas de la red implementada.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: