Las Máquinas de Soporte Vectorial: una explicación completa
En este post veremos una explicación detallada y muy completa de todo lo relacionado con las Máquinas de Vectores de Soporte (o Máquinas de Soporte Vectorial), uno de los algoritmos clásicos del Machine Learning y que en la actualidad es ampliamente usado en combinación con arquitecturas como las Redes Neuronales o las Convolucionales.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción: concepto intuitivo de la clasificación
El principal uso de las Máquinas de Soporte Vectorial se da en la clasificación binaria, es decir para separar un set de datos en dos categorías o clases diferentes.
Para entenderlo, veamos de forma intuitiva este concepto. Supongamos que estamos conformando nuestro propio equipo de ciclismo y debemos seleccionar a nuestros corredores, y que cada ciclista puede pertenecer a una de dos categorías: escalador, es decir especialista en la montaña, o embalador, es decir especialista en las llegadas con terreno plano.
Para asignar la categoría a la que pertenece cada ciclista, es decir para clasificarlo, podemos usar varias características.
Consideremos una primera característica: el peso. Generalmente los ciclistas más livianos son mejores escaladores, y aquellos con más peso tienen más potencial para el embalaje. En este caso podemos definir un umbral y al momento de la clasificación simplemente definimos la categoría dependiendo si el peso del ciclista está a la izquierda o a la derecha de este umbral:
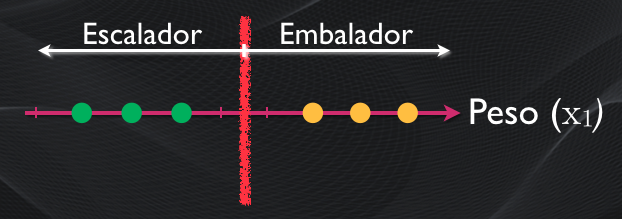
Pero para mejorar la precisión de nuestra clasificación podemos agregar más características. Por ejemplo, si añadimos ahora la potencia que desarrolla el ciclista en cada pedalazo, entonces ahora en dos dimensiones podremos trazar una línea que divida a estos dos grupos:
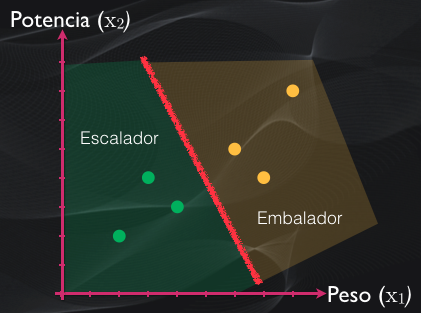
Si además del peso y la potencia incluimos por ejemplo la capacidad pulmonar, entonces tendremos una distribución de puntos en tres dimensiones (es decir tres características), y en este caso tendremos un plano que separa una categoría de otra:
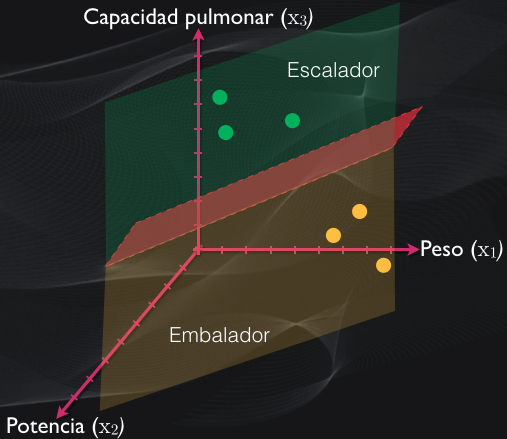
Y con cuatro o más dimensiones no resulta fácil dibujarlo, pero la idea es que en todos los casos idealmente tendremos una frontera de decisión que permite determinar la categoría a la que pertenece cada ciclista.
El hiperplano y la clasificación
En adelante vamos a llamar a esta frontera el hiperplano y para la explicación que viene ahora nos enfocaremos en dos dimensiones, pues resulta más fácil de entender gráficamente. Pero estos mismos conceptos se aplican para una, tres o más dimensiones.
En dos dimensiones, nos enfocaremos en dos características: el peso y la potencia de cada pedalazo. Si volvemos a nuestro grupo inicial de ciclistas, podemos ver que los dos grupos están separados por un hiperplano que en este caso es simplemente una línea recta:
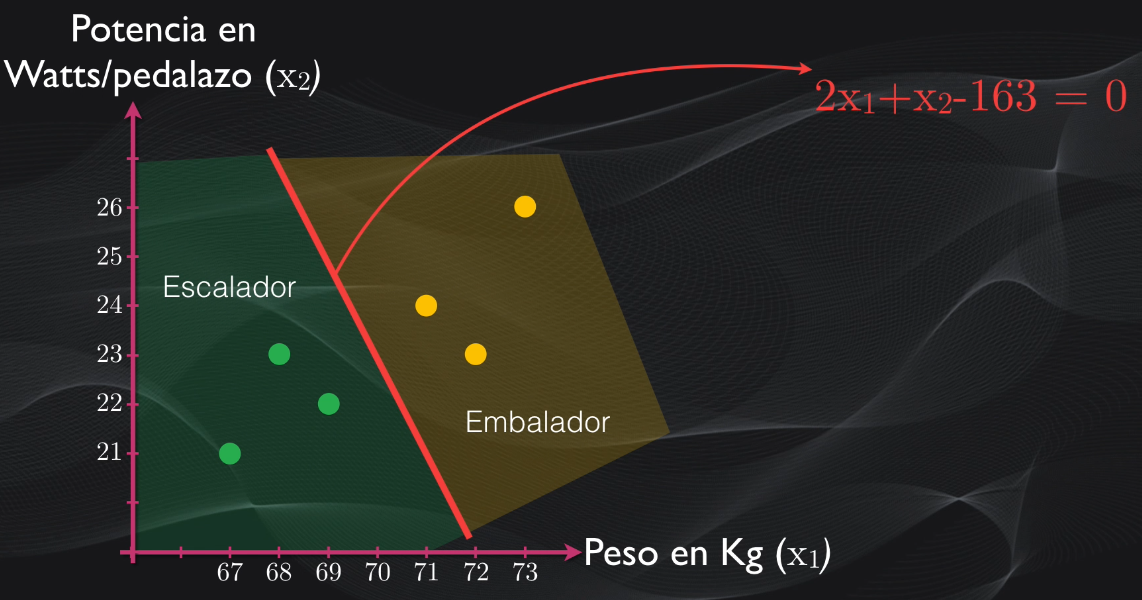
Si analizamos esta línea recta veremos que cualquier punto que pertenezca a ella tiene una característica importante: al reemplazarlo en la ecuación el resultado será exactamente igual a cero:
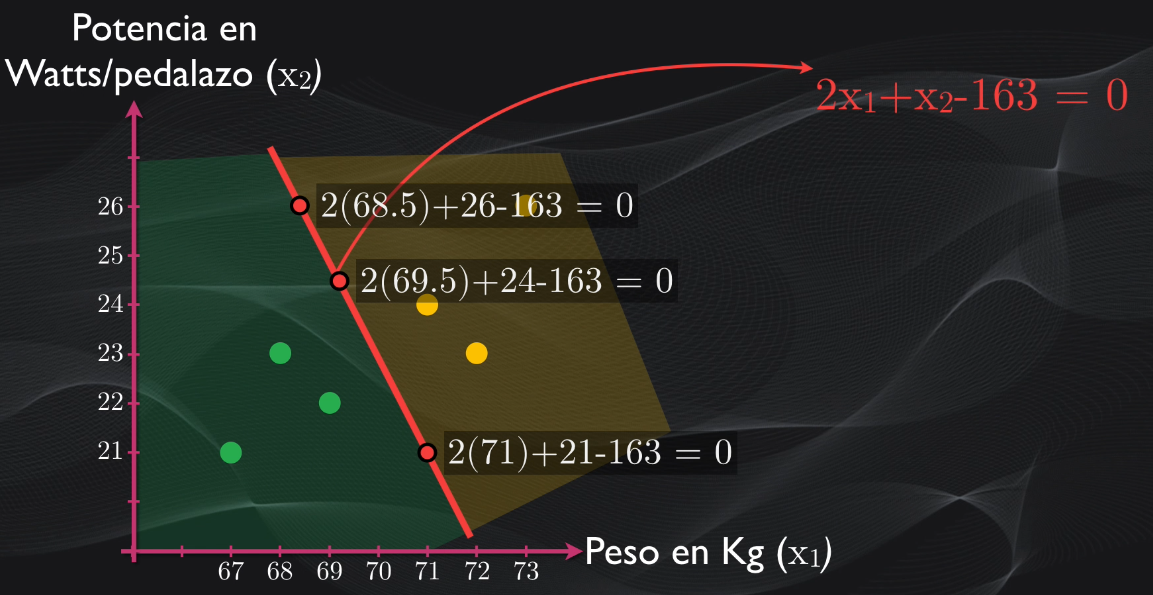
Pero si tomamos por ejemplo los puntos en los cuales están ubicados los embaladores, veremos que al reemplazarlos en la ecuación del hiperplano todos son mayores que cero:
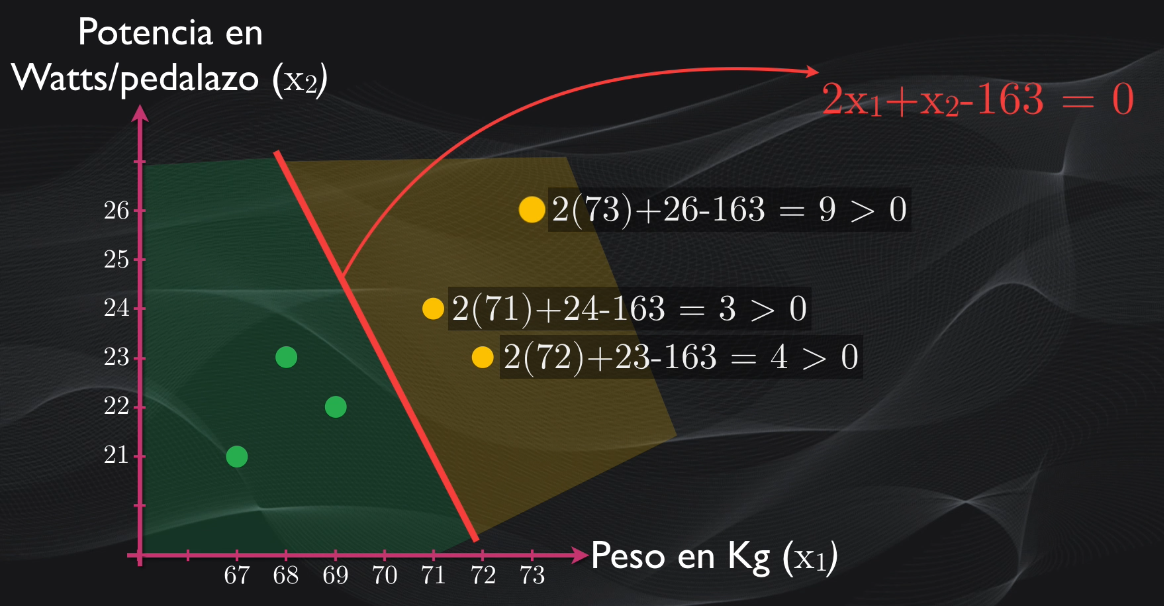
mientras que al hacer lo mismo para los puntos donde están los escaladores se obtienen valores menores que cero:
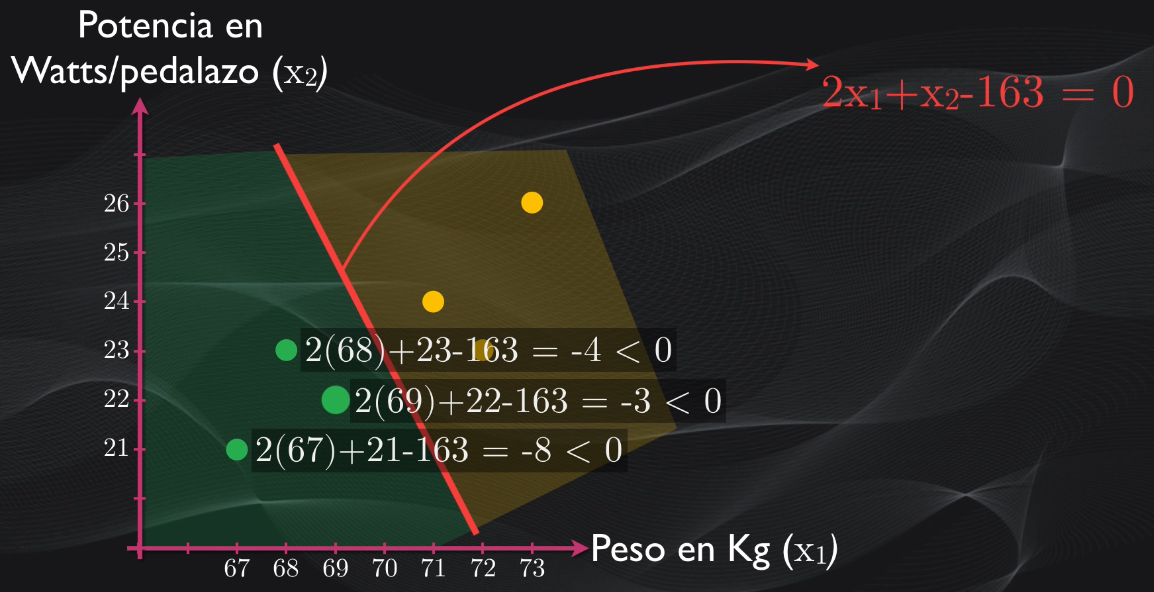
Así que partiendo de esto podemos definir un algoritmo sencillo para realizar la clasificación:
- Obtener la ecuación del hiperplano, lo que equivale a encontrar sus coeficientes
- Por cada dato que deseo clasificar reemplazar sus coordenadas en la ecuación del hiperplano, y dependiendo del valor obtenido clasificar el dato en una u otra categoría.
Si miramos en detalle este sencillo algoritmo veremos que el problema de la clasificación se reduce a encontrar la ecuación de este hiperplano. Y es allí donde entra en juego el algoritmo de Máquinas de Vectores de Soporte.
El mejor hiperplano y las Máquinas de Soporte Vectorial: clasificación “hard margin” (margen duro)
Para entender cómo funciona este algoritmo debemos comprender un concepto muy importante: el de el mejor hiperplano.
Al intentar separar nuestro set de datos podemos obtener diferentes líneas o hiperplanos, y todos ellos logran dividir correctamente el set en dos categorías. Pero, ¿cuál de ellas es mejor?
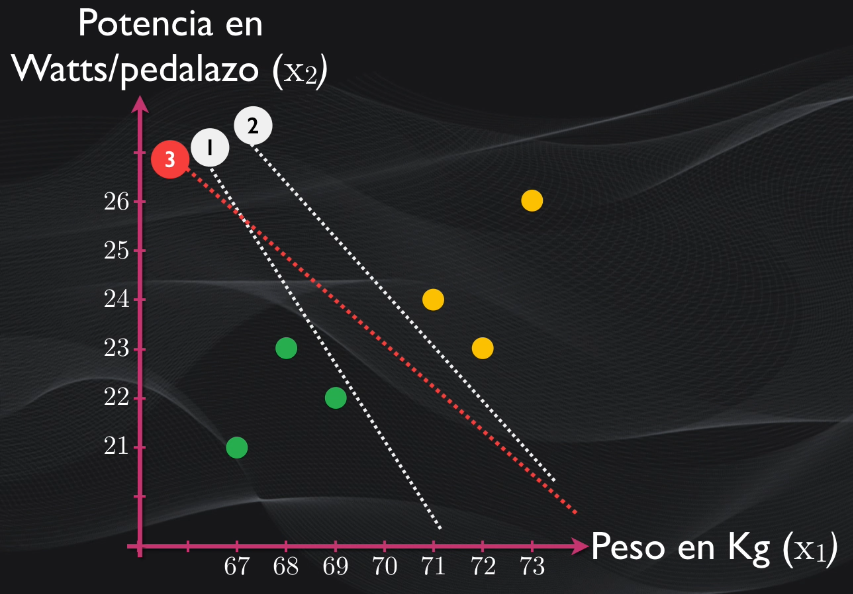
Vemos que las líneas 1 y 2 están demasiado cerca de una de las categorías, mientras que la línea tres está en un punto intermedio entre las dos agrupaciones. Esta línea es precisamente el hiperplano óptimo, pues es la que se encuentra más alejada de todas las observaciones, y esto hace que al momento de clasificar un nuevo dato no exista un sesgo hacia una categoría u otra.
Pues el algoritmo de Máquinas de Soporte Vectorial permite precisamente obtener este hiperplano óptimo.Y aunque existen diferentes maneras de implementarlo computacionalmente, en esencia lo que en el fondo logra hacer este algoritmo es primero detectar los puntos más cercanos entre una clase y otra, luego encuentra la línea que los conecta y finalmente traza una frontera perpendicular que divide esta línea en dos. La línea que se obtiene es precisamente el hiperplano óptimo:
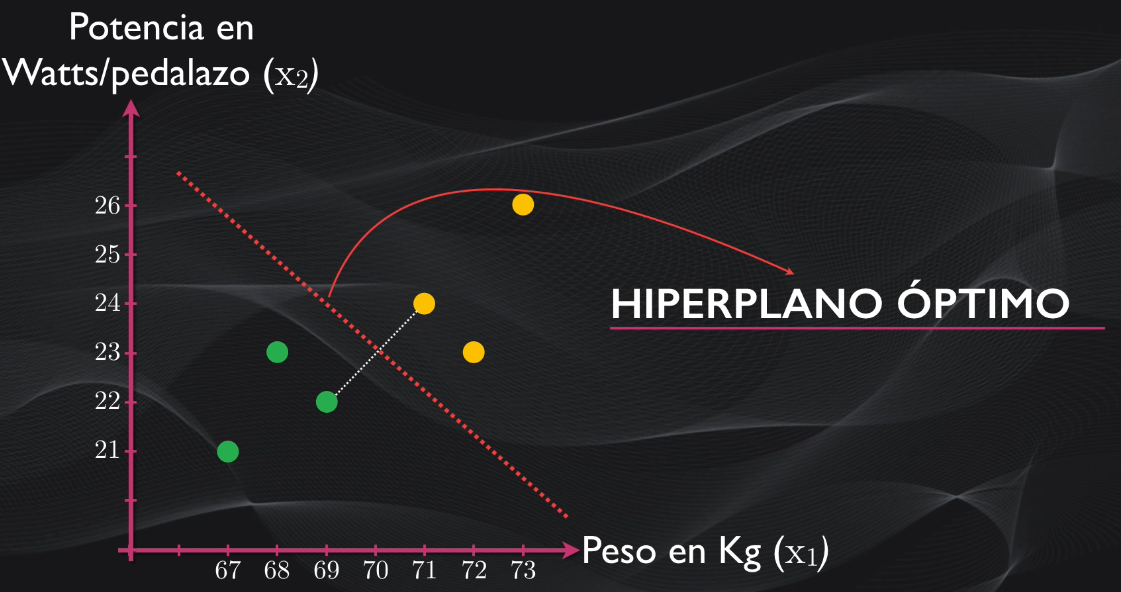
Y acá debemos resaltar tres definiciones importantes:
- Los vectores de soporte, que son precisamente los puntos más cercanos entre una clase y otra, y son los que le dan el nombre al algoritmo:
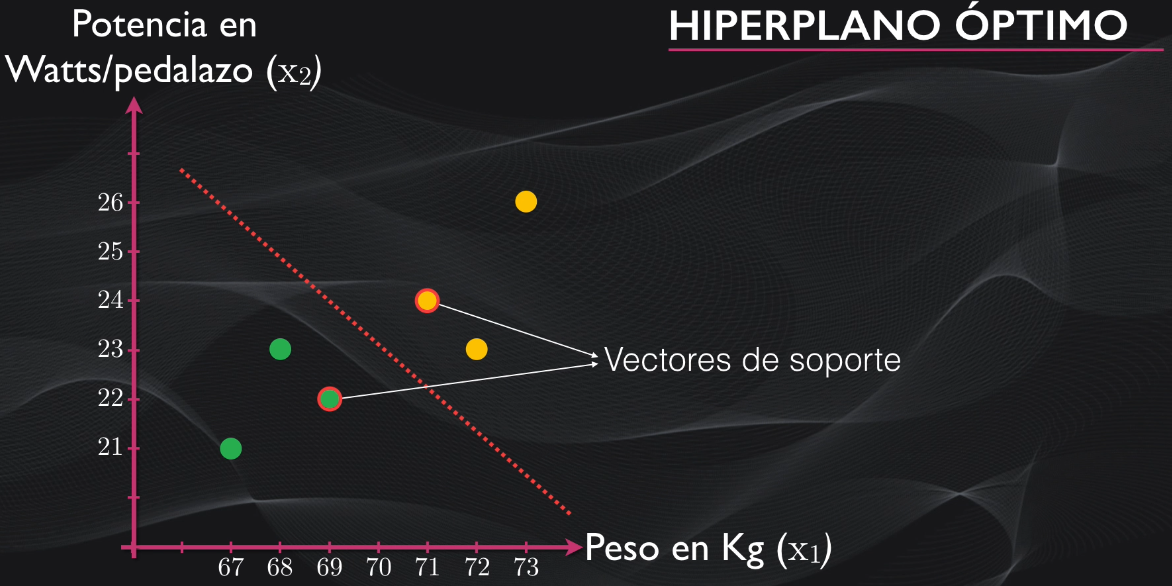
- El margen, que es la distancia entre el hiperplano y los vectores de soporte:
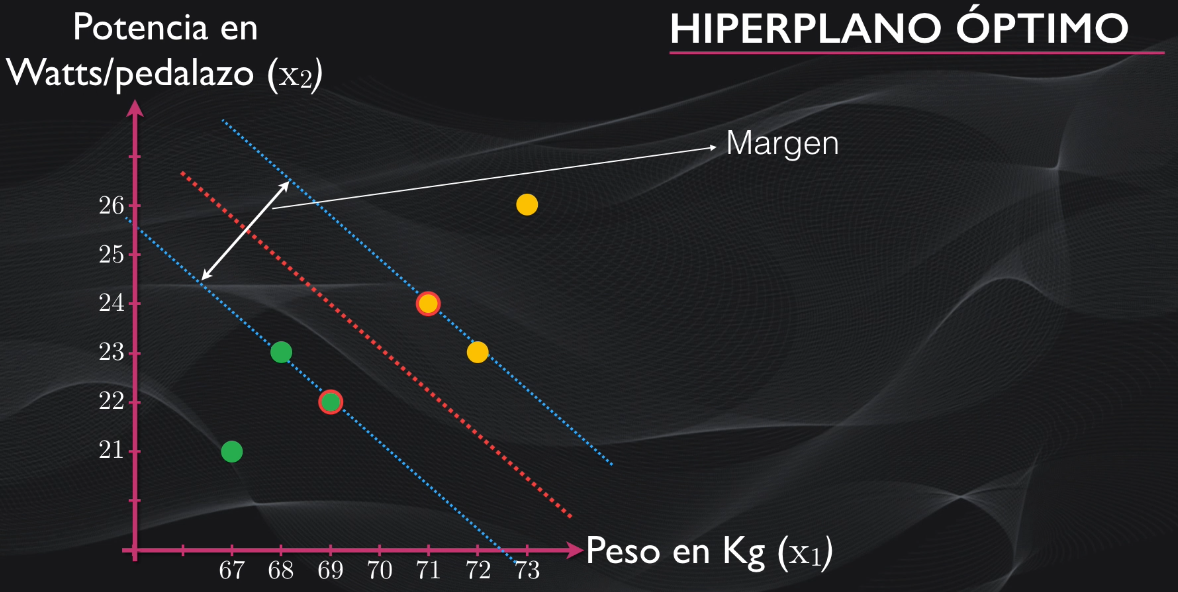
- Y el mismo hiperplano óptimo que es la frontera de separación que consigue el mayor margen posible:
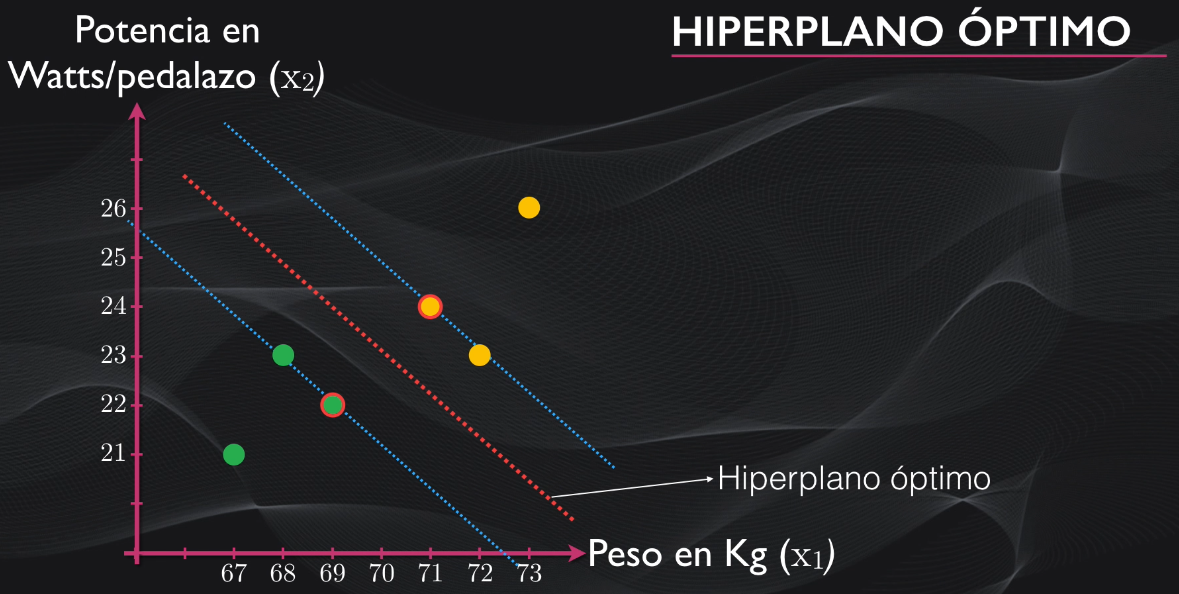
Así que podemos pensar en el algoritmo de Máquinas de Soporte Vectorial como un método que nos permite trazar una carretera con dos carriles entre nuestros datos: el hiperplano óptimo es el separador entre uno y otro carril, y el margen es el ancho de cada carril (que es igual en ambos casos). Y la idea de las Máquinas de Soporte Vectorial es precisamente obtener los carriles más anchos posibles.
Presencia de outliers y el parámetro C: clasificación “soft margin” (margen suave)
Bien, con esto ya tenemos el principio básico de cómo funcionan las Máquinas de Vectores de Soporte. Pero este algoritmo funciona sólo para el caso ideal, en el que nuestros datos están perfectamente separados y podemos usar una línea recta o frontera de decisión óptima, es decir con un margen bastante amplio.
Pero, volviendo a nuestro ejemplo, qué pasaría si llega a nuestro equipo un corredor excepcional, que se destaca en la montaña pero que también es muy buen embalador. En este caso ese nuevo corredor se comporta como un outlier o valor atípico, pues no obedece al comportamiento esperado para un escalador:
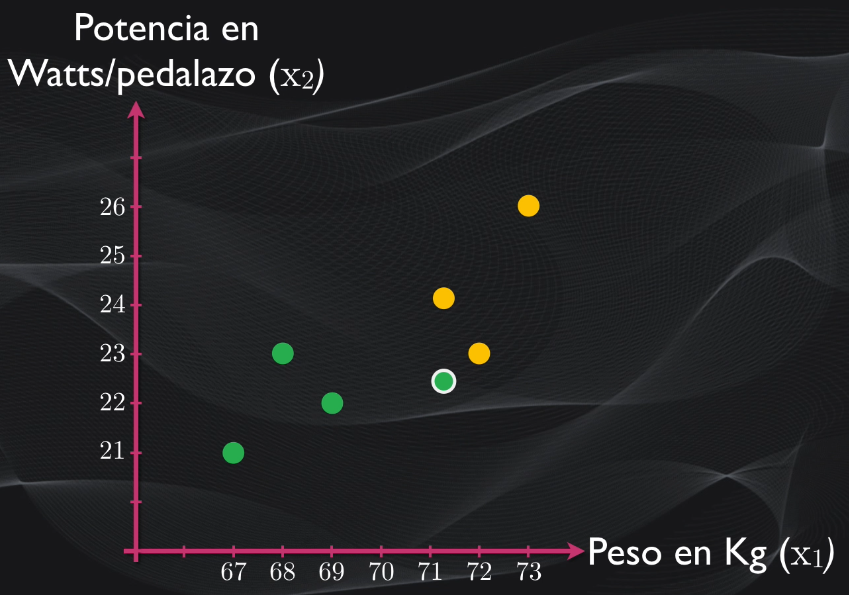
Si aplicamos el algoritmo explicado anteriormente veremos que se obtendrá un hiperplano óptimo pero que el margen será muy pequeño. Esto se debe a que los vectores de soporte están más cerca. Y esto puede llevar al overfitting: es decir que si introducimos un dato nuevo, que no haya sido nunca visto por el algoritmo, muy probablemente será clasificado incorrectamente porque el margen es muy reducido y no hay una adecuada separación entre las clases:
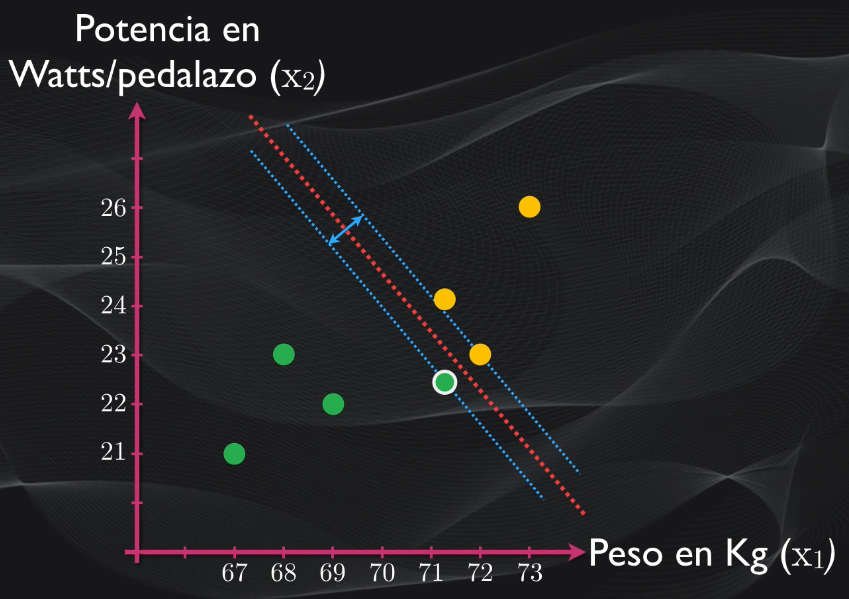
Así que el algoritmo que vimos en la sección anterior, conocido como hard margin (o margen duro) no resulta muy flexible y no es ideal usarlo si hay outliers como el de nuestro corredor excepcional.
La manera de resolver esto es ensanchando el margen, permitiendo que la mayoría de los datos estén clasificados correctamente, y aceptando la posibilidad de que existan unos cuantos errores al momento de la clasificación.
Esto se logra modificando el algoritmo para obtener el hiperplano óptimo: originalmente en el clasificador hard margin se buscaba maximizar el margen, y para esto se modificaban únicamente los coeficientes del hiperplano:
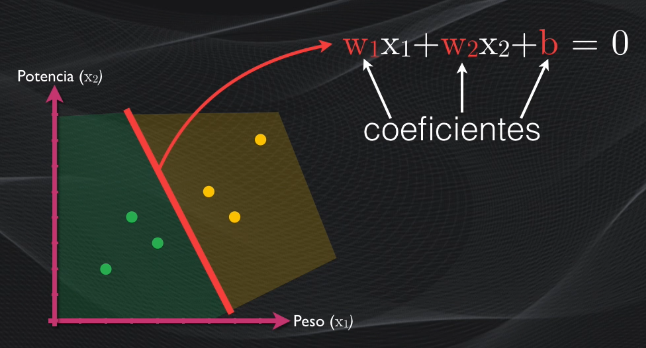
Ahora, para contrarrestar el efecto del outlier, se incluye un término adicional a esta función, lo que permite flexibilizar el margen. Este término depende de un parámetro C, un hiperparámetro, que yo como diseñador elijo durante el entrenamiento. La idea es que un C relativamente pequeño permite generar márgenes amplios, y a medida que su tamaño aumente el margen se va reduciendo poco a poco:
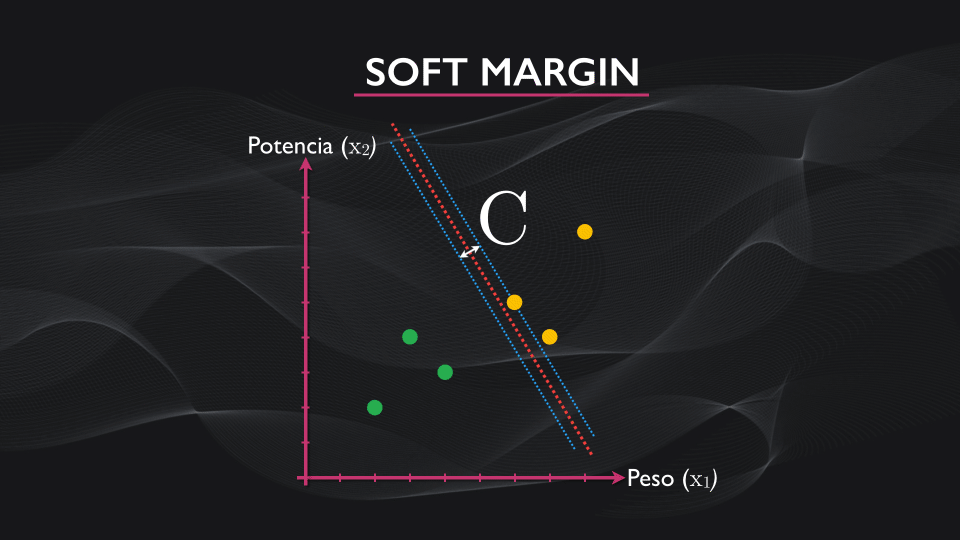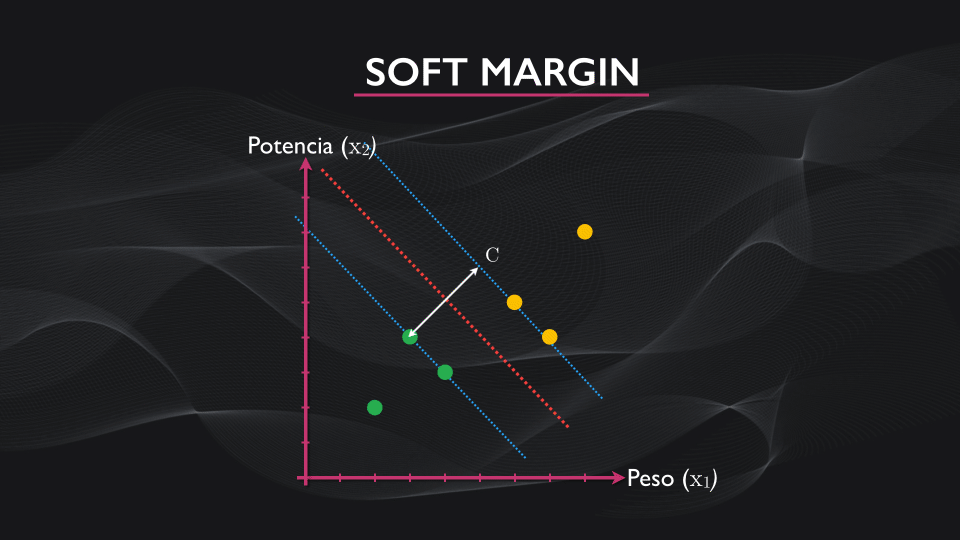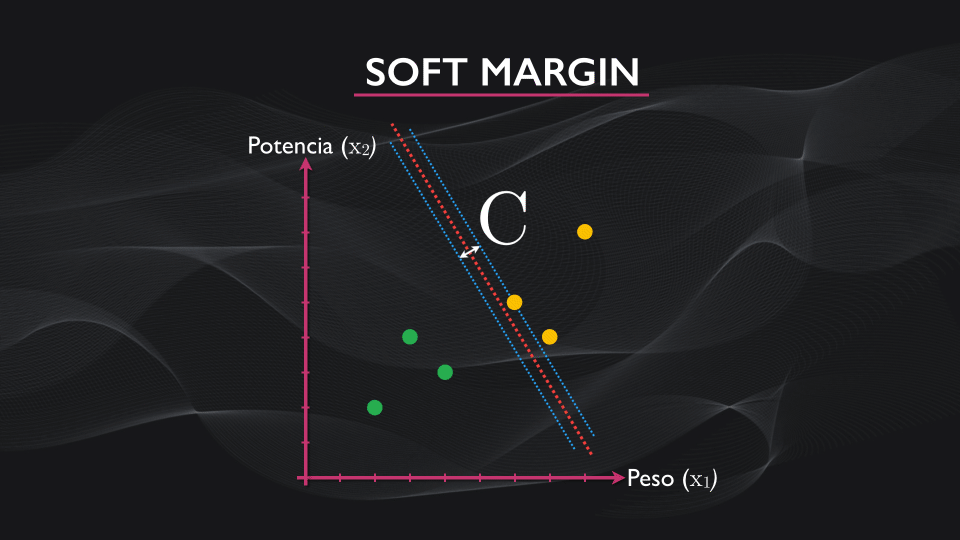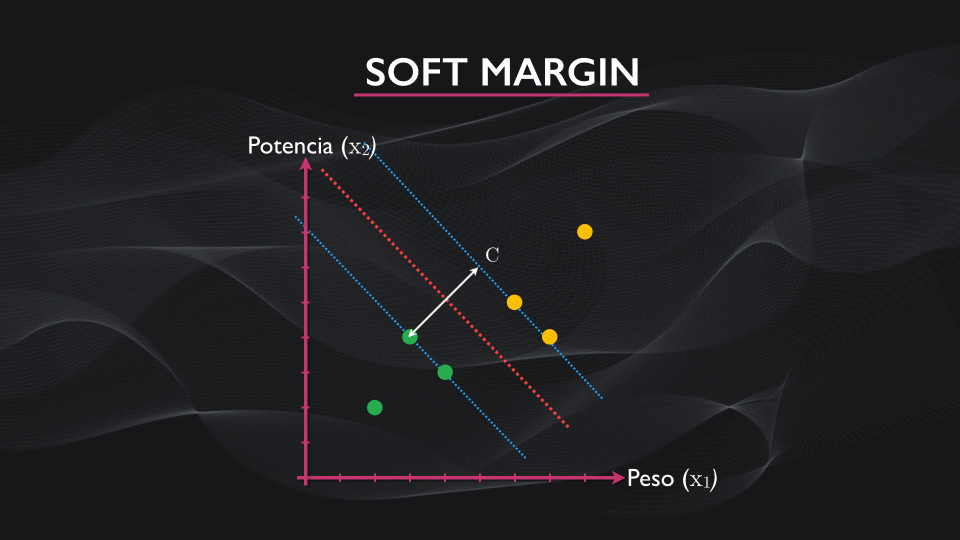
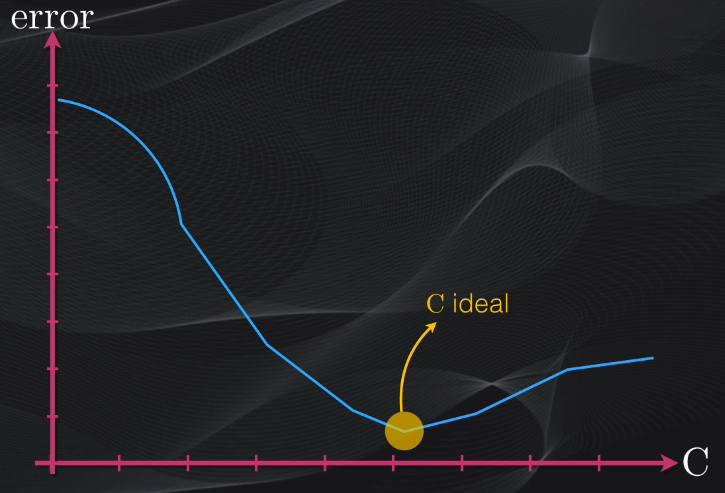
Este parámetro se escoge de manera empírica analizando el error que se obtiene en la clasificación vs. diferentes valores de C, y a este algoritmo de máquina de vectores de soporte se le conoce como “soft margin”:
## Máquinas de Soporte Vectorial no lineales: el truco del Kernel
Bien, ya tenemos un clasificador mucho más versátil y sobre el cual tenemos algún tipo de control al momento de obtener el margen. Pero todavía estamos considerando una situación bastante ideal: la mayoría de los datos están lo suficientemente separados y basta trazar una simple línea recta para poder clasificar correctamente a la mayoría de ellos.
Pero en casos reales, la situación es más complicada. Las fronteras de división usualmente no son líneas rectas sino que tienen formas mucho más complejas. Y el problema es que, hasta donde hemos visto, las máquinas de soporte vectorial sólo permiten obtener hiperplanos o fronteras de decisión lineales. Entonces, ¿Qué se puede hacer en este caso?

Una alternativa sería agregar más dimensiones a cada dato. Es decir, ¿qué pasaría si encontramos una forma de agregar una o más dimensiones adicionales para así lograr separar las dos categorías? En este caso podríamos usar el mismo algoritmo de máquinas de vectores de soporte para clasificar los datos en esas tres dimensiones:
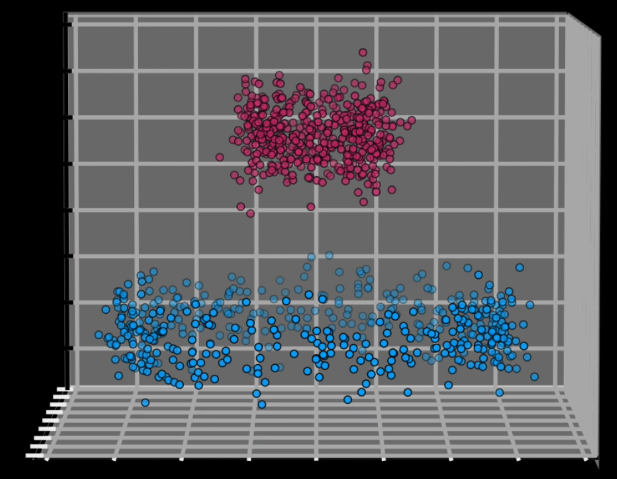
¿Pero cómo logramos agregar más dimensiones a los datos para así lograr su clasificación? Pues el método usado en las máquinas de soporte vectorial se conoce como el Truco del kernel. Básicamente consiste en tomar el set de datos original, que no es separable, y mapearlo a un espacio de mayores dimensiones usando una función no lineal (en un momento veremos las funciones más usadas):
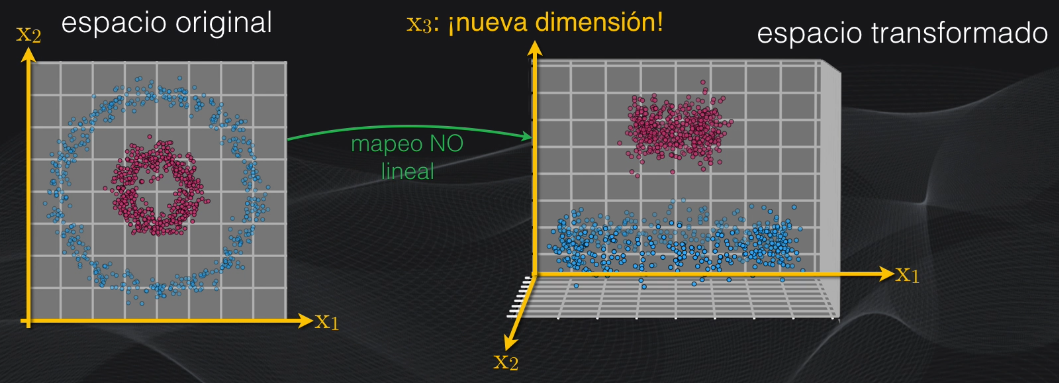
La idea es que con esta transformación el dataset ahora será separable linealmente, es decir que se puede usar una máquina de vectores de soporte tipo soft margin, como la que vimos anteriormente, para obtener el hiperplano óptimo. Una vez lo hayamos obtenido hacemos la transformación inversa, para volver al espacio original, y así llevar a cabo la clasificación:
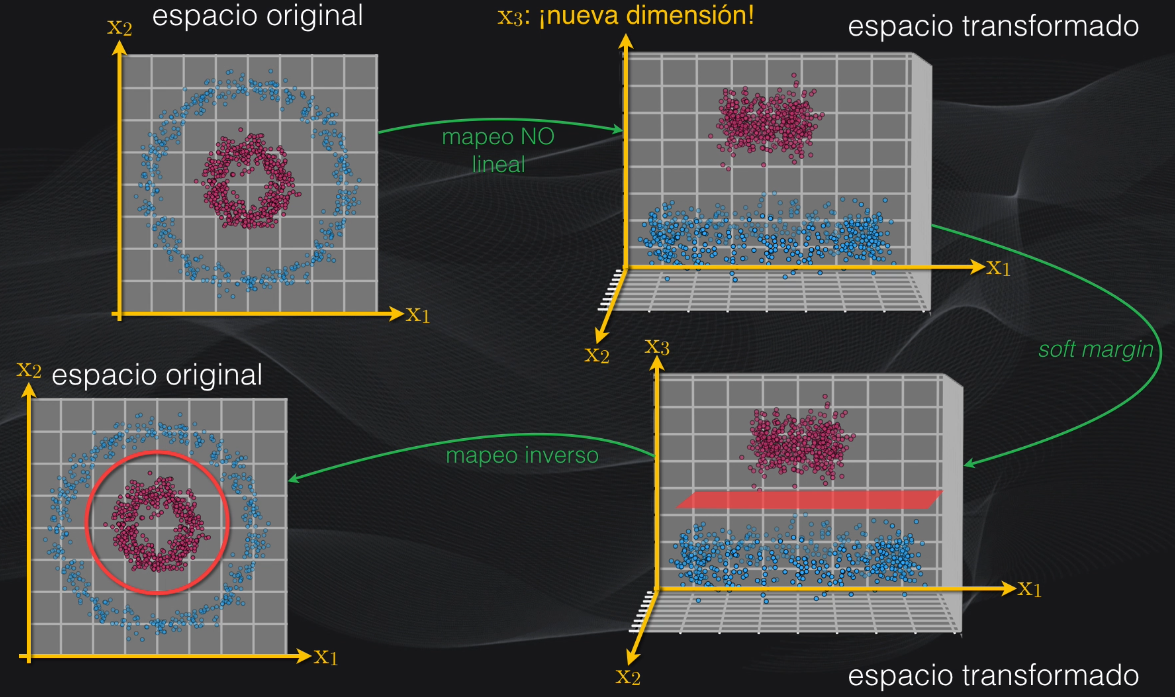
En la práctica el truco del Kernel no implementa todos estos pasos, sino que realiza este mapeo y el cálculo del hiperplano de una manera simplificada, usando algo de álgebra lineal para evitar demasiadas operaciones y hacer más rápido el algoritmo.
Las transformaciones más usadas en este truco del kernel se logran usualmente a través de dos tipos de funciones:
- Las polinomiales, que implican obtener combinaciones de los vectores de características usando potencias mayores que 1, o
- Usando funciones gaussianas, con forma de campana, que se conocen como funciones de base radial.
En cualquiera de estos casos, y dependiendo del set de datos, lo que se logra es añadir más dimensiones a los datos originales para, en este espacio de más dimensiones, lograr la separación lineal de los datos.
Aplicaciones
Aunque las Máquinas de Soporte Vectorial fueron desarrolladas a comienzos de los años 90, aún son muy usadas en la actualidad pues permiten separar de manera óptima dos agrupaciones de datos, logrando crear una frontera de decisión que está a la misma distancia de ambas agrupaciones.
Esto hace que una Máquina de Vectores de Soporte tenga usualmente una precisión más alta que un perceptrón o neurona artificial. De hecho esto ha permitido que en la actualidad sea común encontrar sistemas de procesamiento de imágenes, como por ejemplo para el reconocimiento facial, que extraen características de las imágenes usando redes convolucionales y que luego alimentan estas características a una Máquina de Soporte Vectorial para realizar la clasificación final del rostro.
Conclusión
Bien, con esto espero que tengan una idea detallada de qué son y cómo funcionan las Máquinas de Soporte vectorial. En un próximo video veremos un tutorial sobre cómo usarlas para resolver un problema de Machine Learning en Python.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: