Padding, strides, max-pooling y stacking en las Redes Convolucionales
En este tercer post de la serie “Redes Convolucionales” hablaremos de cuatro operaciones esenciales para entender este tipo de redes: el padding, los strides, el max-pooling y el stacking. Con esto tendremos las bases necesarias para entender el funcionamiento de cualquier Red Convolucional.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
Como vimos en el post anterior, la convolución es una operación usada en las Redes Convolucionales y que permite extraer características de la imagen procesada.
Adicional a esto usamos las operaciones de padding, strides, max-pooling y stacking para tomar dichas características y obtener una representación compacta (es decir con menos datos) de las mismas, lo que facilita el posterior proceso de clasificación de la imagen.
A continuación hablaremos en detalle de cada una de estas operaciones.
El padding
Recordemos que la convolución genera una imagen resultante de un menor tamaño que la imagen original. Pues el padding se usa para lograr que la imagen resulatnte y la original tengan el mismo tamaño.
Así, el padding consiste simplemente en agregar pixeles con valor igual a cero a los bordes de la imagen original:

Esto permite que al realizar la convolución, la imagen resultante sea del mismo tamaño que la imagen original:

Aunque no es muy usado, en ocasiones el padding se implementa en algunas capas de las Redes Convolucionales, pues al mantener el tamaño de la imagen entre una capa y otra es posible crear redes más profundas, lo que a su vez permite extraer características más específicas de las imágenes durante el entrenamiento.
Los strides
En la convolución original, el kernel se desplaza un pixel hacia la derecha, o hacia abajo, durante cada iteración. Cada uno de estos desplazamientos se conoce como stride (o salto), y en la convolución original este valor es igual a 1:

Sin embargo, también es posible realizar la convolución con strides mayores, lo que permite obtener imágenes resultantes de menor tamaño en comparación con las obtenidas en la convolución original:

En las redes convolucionales esto es útil, pues reduce la cantidad de datos a procesar entre una y otra capa de la red.
Padding y strides combinados
Es posible usar el padding y los strides de manera simultánea durante la convolución.
Por ejemplo, si usamos un padding de 1, un filtro de 3x3 y un stride de 2, obtendremos una imagen de 3x3:

Max-pooling
El pooling es una operación que permite analizar el contenido de una imagen por regiones (o bloques) para extraer la información más representativa de las mismas.
Al igual que el uso de strides, el max-pooling permite reducir la cantidad de datos entre una capa y otra, facilitando así el procesamiento de las imágenes y el entrenamiento de la red, pero a la vez preservando la información más relevante.
En el caso del max-pooling la imagen es dividida en regiones del mismo tamaño, y para cada región se extrae simplemente el valor máximo que corresponderá a un pixel en la imagen resultante.
Por ejemplo, a la imagen de 6x6 mostrada en la figura de abajo, aplicamos un filtro max-pooling de 2x2. Esto quiere decir que resultarán 9 diferentes regiones dentro de la imagen:

Y para cada una de estas 9 regiones se obtiene el valor máximo y se asigna dicho valor al pixel correspondiente en la imagen de salida:

Stacking
Al analizar la convolución vimos cómo el uso de un kernel permite extraer características relevantes de una imagen (como líneas verticales u horizontales, bordes, esquinas, o formas más complejas), donde por cada kernel utilizado se obtiene una imagen resultante.
Sin embargo, en las Redes Convolucionales, lo que nos interesa es obtener múltiples características de una imagen y, por lo tanto, usamos múltiples filtros.
El stacking es simplemente el resultado de apilar múltiples imágenes resultantes, provenientes de la convolución con múltiples filtros.
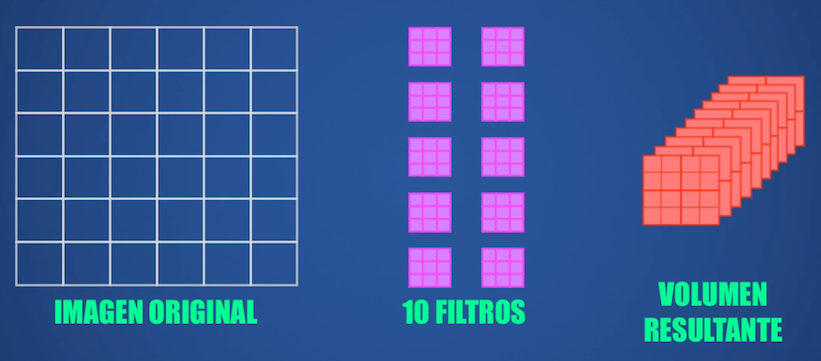
Así por ejemplo, si la imagen de entrada es de 6x6 y usamos 10 kernels de 3x3 para extracción de características (sin padding y con stride igual a 1) entonces la imagen resultante de aplicar cada filtro será de 4x4. Pero al aplicar todos los filtros y usar el stacking tendremos un volumen resultante con un tamaño de 4 filas, 4 columnas y una profundidad de 10, esta última correspondiente a cada uno de los filtros usados:
Conclusión
Bien, hemos visto cuatro operaciones básicas que se realizan dentro de una Red Convolucional: el padding, los strides, el max-pooling y el stacking. Estas operaciones, combinadas con la convolución y con funciones de activación, las que permiten extraer de forma efectiva características relevantes de una imagen usando una red convolucional.
Con todos estos elementos ya tenemos lo esencial para entender cómo están conformadas las Redes Convolucionales. Así que en el próximo post de esta serie veremos cómo combinar todas estás ideas para implementar un clasificador de imágenes con Redes Convolucionales, usando LeNet, la arquitectura precursora de las Redes Convolucionales que se usan hoy en día.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:
Te invito además a revisar los otros posts de esta serie: