¿Qué son las Redes LSTM?
En este cuarto post de la serie “Redes Neuronales Recurrentes” veremos en detalle el funcionamiento de las Redes LSTM, la principal arquitectura de Redes Recurrentes y la más usada en la actualidad.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
En los posts anteriores hablamos de las Redes Neuronales Recurrentes básicas, y vimos incluso un ejemplo de cómo una de estas redes podía ser entrenada, por ejemplo, para la [generación de texto].
Sin embargo vimos que esa arquitectura presentaba un inconveniente: a pesar de contar con una memoria, esta era de corto plazo, y por eso la red implementada funcionaba bien solo cuando el nombre generado era relativamente corto (de unos cuantos caracteres).
En primer lugar veremos las limitaciones de las redes recurrentes básicas, y luego analizaremos en detalle una red LSTM y entenderemos por qué estas redes son más robustas y permiten contar con una memoria de mucho más largo plazo.
Las limitaciones de las Redes Neuronales Recurrentes
Primero hablemos de las limitaciones de memoria que tienen las redes neuronales recurrentes vistas anteriormente.
Una [Red Recurrente básica] tiene dos entradas: el dato actual y el estado oculto anterior. Y proporciona dos salidas: la predicción y el valor actualizado del estado oculto.
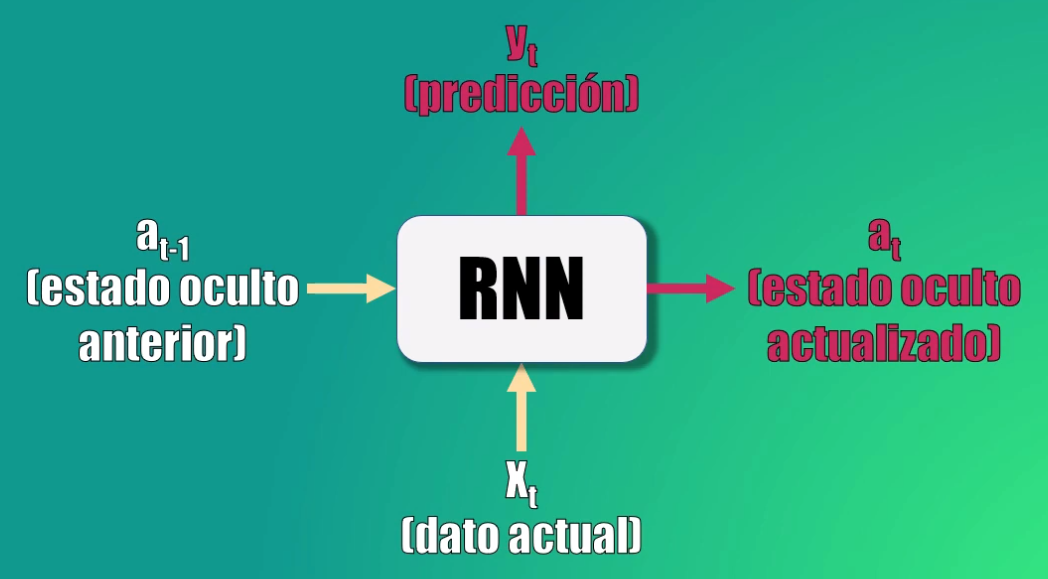
La idea es que la red recurrente está en capacidad de analizar una secuencia de datos de entrada (x) y producir una predicción (y).
Para esto, recordemos que primero la red toma el estado oculto anterior, así como la entrada x, y genera el nuevo estado oculto, usando una transformación lineal y la función de activación tangente hiperbólica.
Después genera la predicción, tomando el nuevo estado oculto y aplicando otra transformación que es posteriormente llevada a una función softmax.
Para entender porqué la red recurrente tiene una memoria de corto plazo veamos cómo el estado oculto inicial (a0) afecta el cálculo la predicción final de nuestro ejemplo (y3). Para simplificar este análisis nos enfocaremos únicamente en el efecto que tienen los estados ocultos en la salida, olvidando por un momento el efecto que la entrada y el parámetro “b” tienen en el cálculo exacto de cada uno de estos estados.
Para calcular y3 tomamos el estado oculto 3, lo multiplicamos por el parámetro de la red y lo llevamos a la función softmax.
Este estado oculto 3 se calcula a partir del estado oculto 2, que a su vez depende del estado 1 y del estado cero.
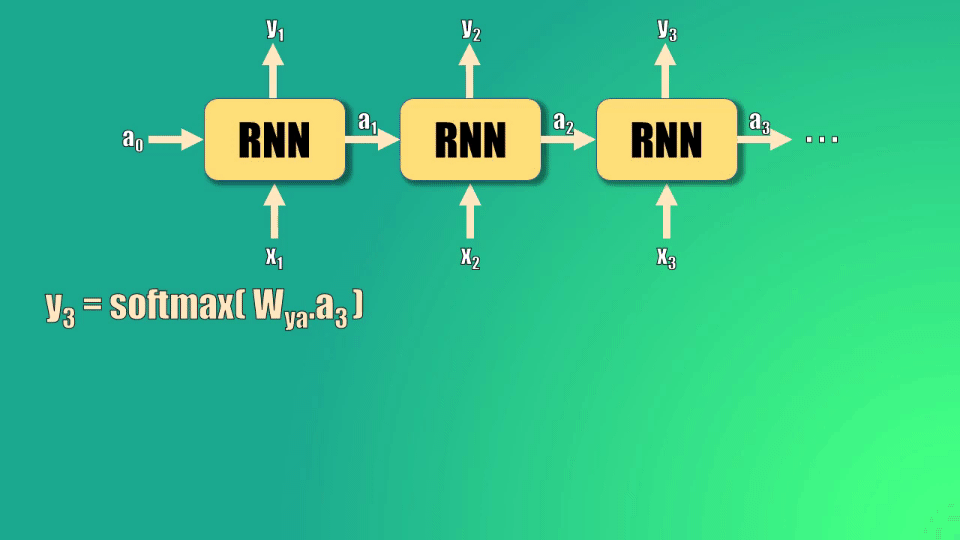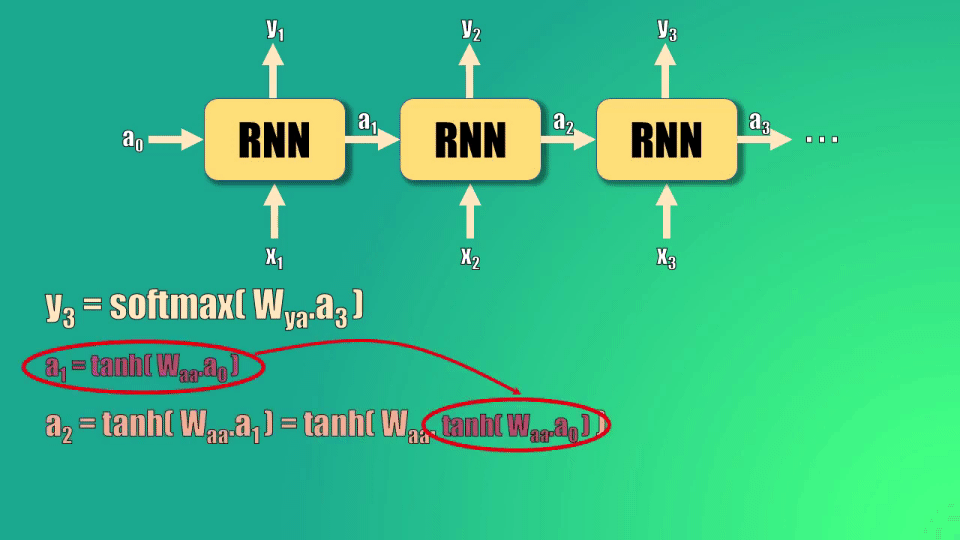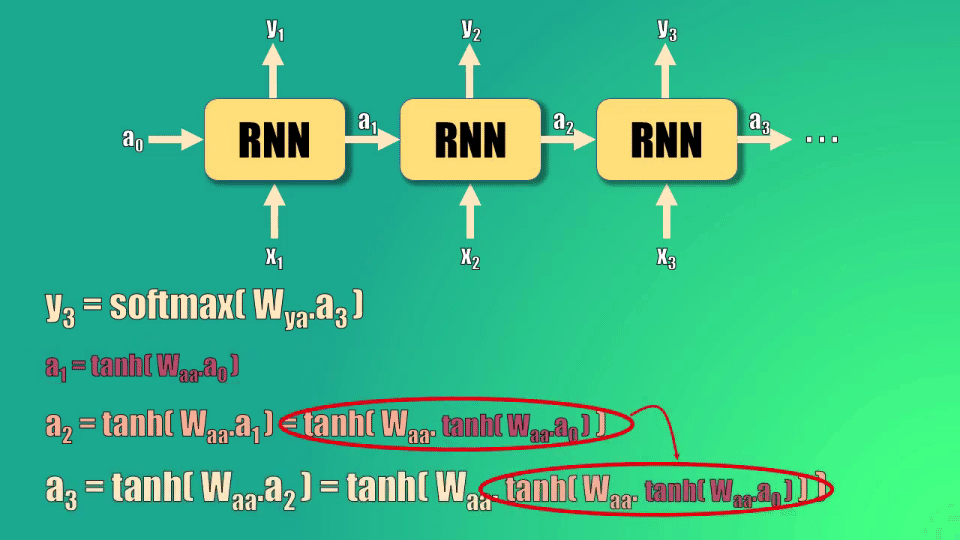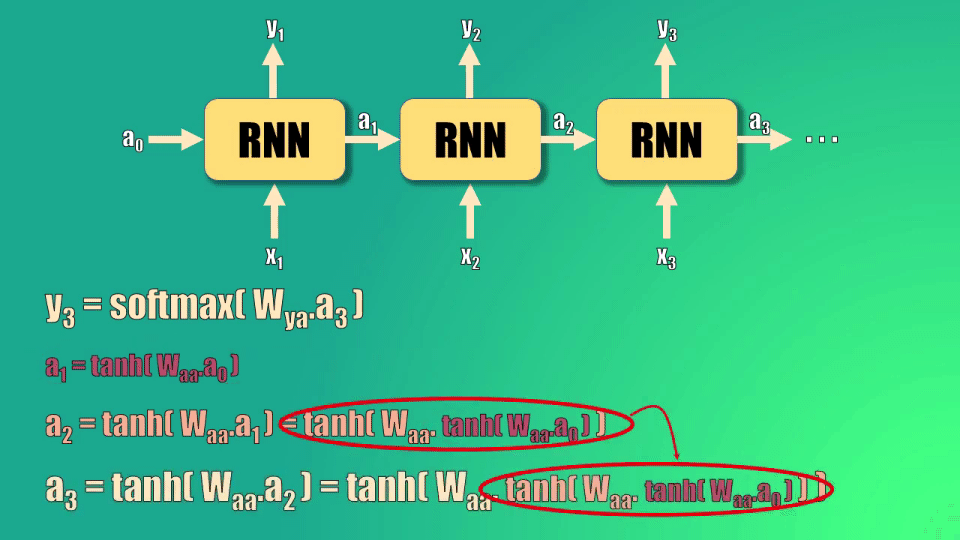
Así, podemos ver la relación que existe entre la predicción y3 y el estado oculto inicial: este estado oculto debe pasar por tres funciones tangente hiperbólica y una función softmax para generar la predicción:
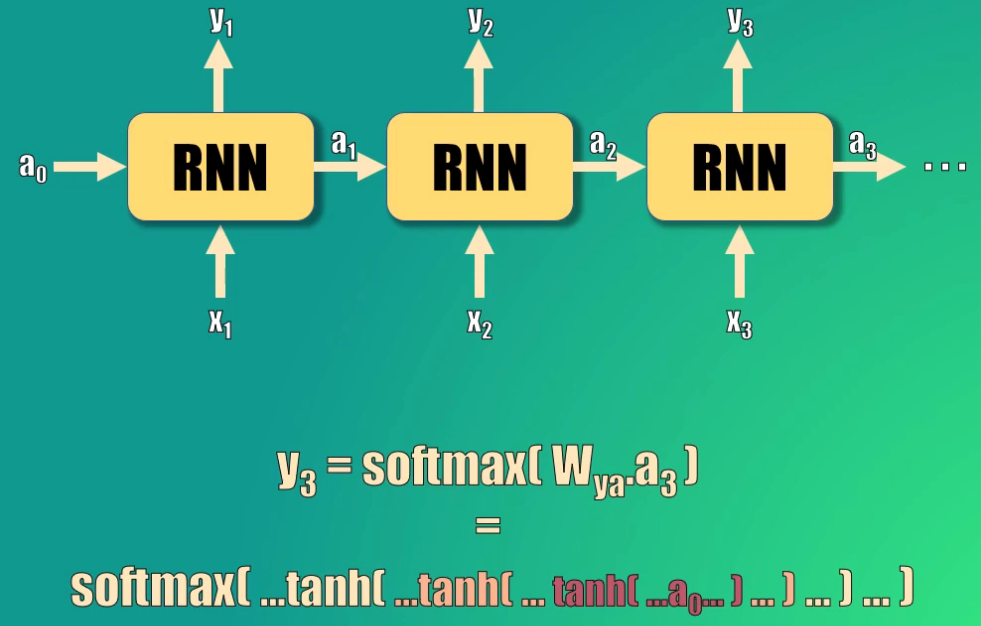
El resultado de esto es que la activación inicial (a0) terminará siendo escalada por un valor mucho menor a 1 al llegar a la salida, puesto que las funciones tangente hiperbólica están anidadas (es decir una dentro de la otra) y estas tienen un valor que en el mejor de los casos es cercano a uno.
Esto quiere decir que el efecto que a0 tendrá en el cálculo de la salida 3 será mínimo, y este efecto empeora si consideramos una secuencia de salida aún mayor.
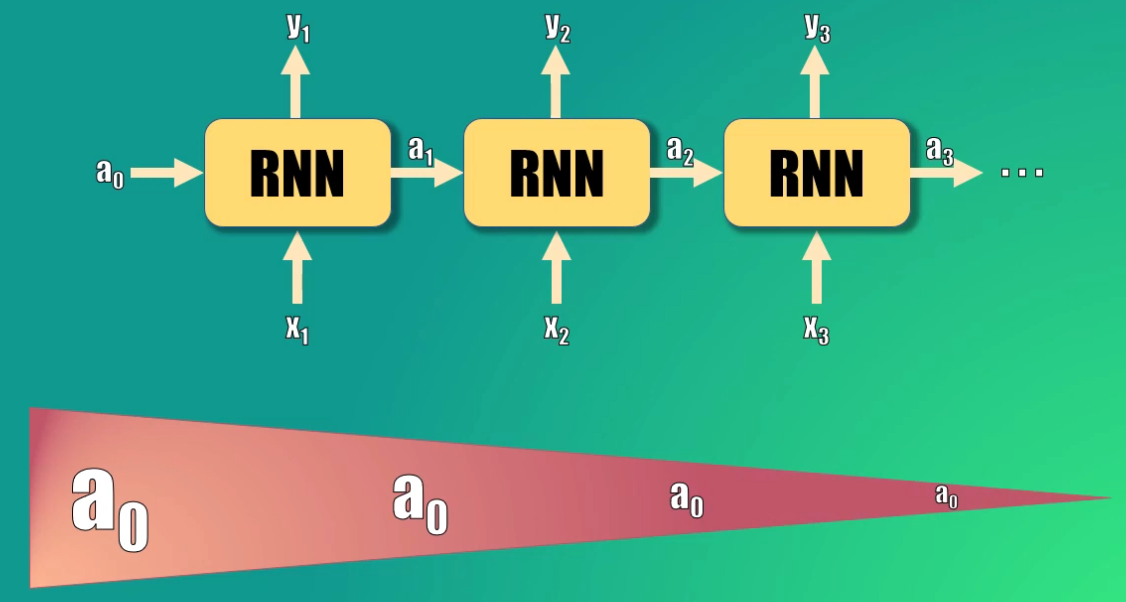
Esto es lo que hace precisamente que una Red Recurrente básica tenga una memoria de corto plazo: la secuencia procesada debe ser relativamente corta para que las activaciones anteriores (es decir la memoria de la red) tenga un efecto relevante en la predicción actual.
Es por esto que en el post anterior, en donde aprendimos a [generar nombres de dinosaurios], veíamos que si el nombre generado era corto se parecía más a un nombre real de dinosaurio, y que a medida que la secuencia generada era más larga los nombres generados parecían más aleatorios.
Las Redes LSTM (del Inglés long short-term memory) resuelven este inconveniente. Veamos entonces cómo funcionan.
Estructura de una red LSTM
Una Red LSTM es capaz de “recordar” un dato relevante en la secuencia y de preservarlo por varios instantes de tiempo. Por tanto, puede tener una memoria tanto de corto plazo (como las Redes Recurrentes básicas) como también de largo plazo.
Funciona de forma similar a como nuestro cerebro analiza las secuencias. Si por ejemplo deseamos comprar un par de audífonos y leemos alguna valoración hecha por un comprador, para tomar la decisión no nos enfocamos en la totalidad del texto: en lugar de ello nos enfocamos únicamente en las palabras que consideramos relevantes, y desechamos el resto de la información.

Las redes LSTM funcionan de manera similar, y están en capacidad de añadir o eliminar la información que consideren relevante para el procesamiento de la secuencia.
Veamos cada elementos que conforma una Red LSTM.
Una celda LSTM
Comparado con una celda de red recurrente básica, la celda LSTM tiene una entrada y una salida adicional. Este elemento adicional se conoce como celda de estado:

Esta celda de estado es la clave del funcionamiento de las Redes LSTM. La celda de estado es como una banda transportadora a la que se pueden añadir o de donde se pueden remover datos que no queremos que queden en la memoria de la red:

Las compuertas
Para añadir o remover datos de esta memoria usamos varias compuertas: forget gate (que permite eliminar elementos de la memoria), la update gate (que permite añadir nuevos elementos a la memoria) y la compuerta de salida (que permite crear el estado oculto actualizado):
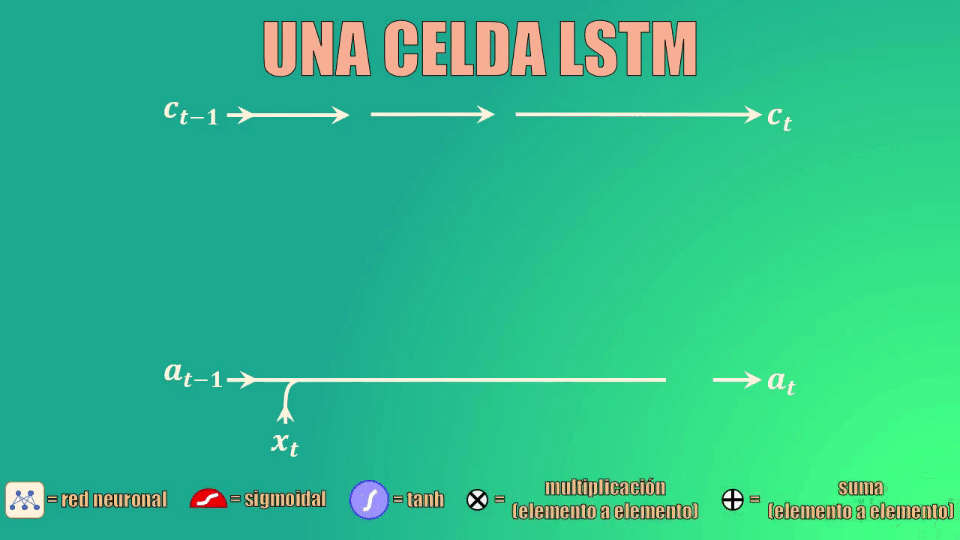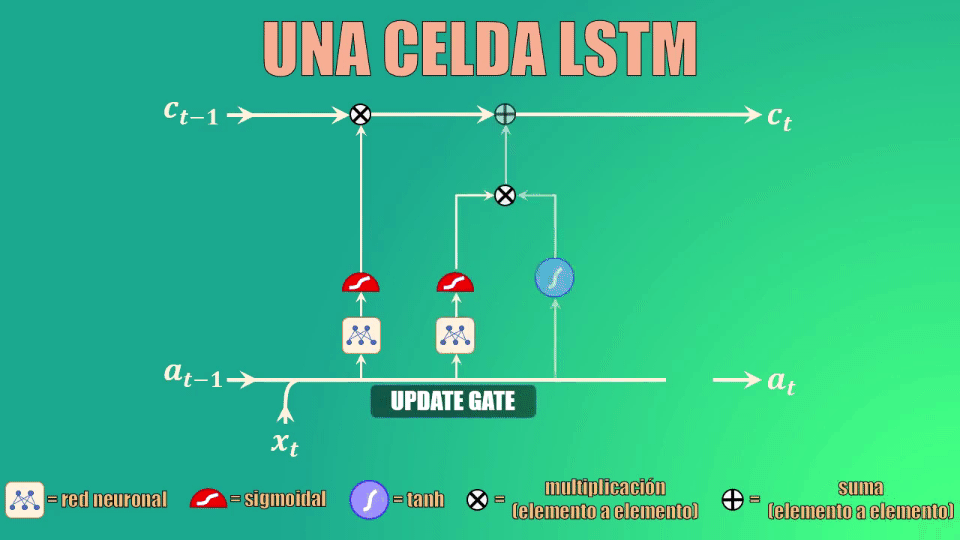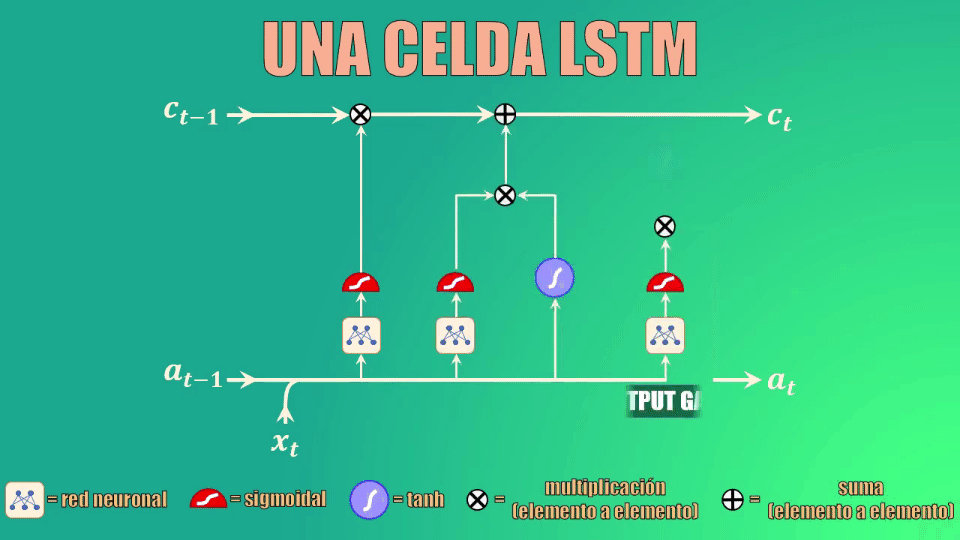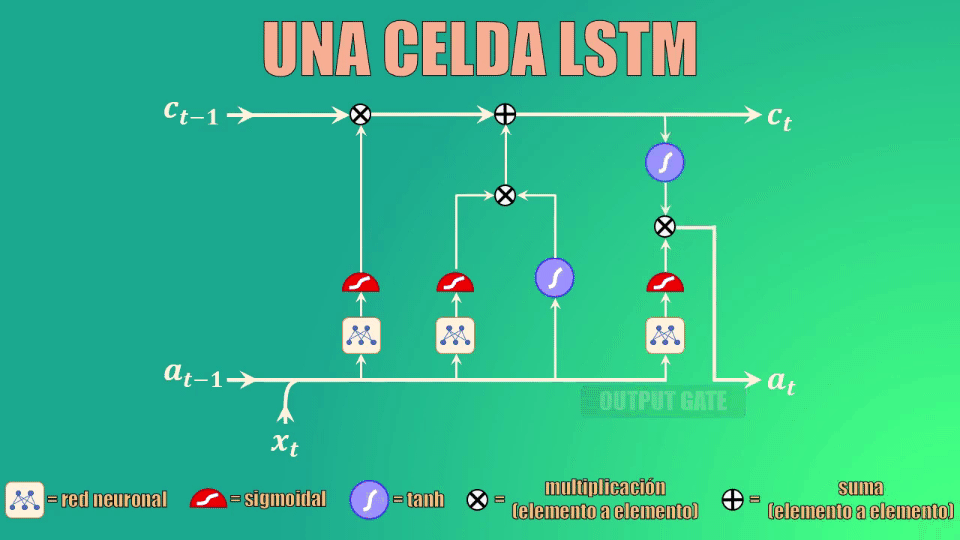
Estas compuertas son redes neuronales que funcionan como válvulas: totalmente abiertas permiten el paso de información, y totalmente cerradas lo bloquean por completo.
Cada una de estas compuertas (o válvulas) está conformada por tres elementos: una red neuronal, una función sigmoidal y un elemento multiplicador.
La función sigmoidal es precisamente la que da a la compuerta el comportamiento de válvula, pues al alcanzar valores entre 0 y 1 permite anular por completo los valores de entrada (si la salida es 0, lo que equivale a una válvula cerrada) y permitir el paso de los mismos (si la salida es 1, lo que equivale a una válvula totalmente abierta):
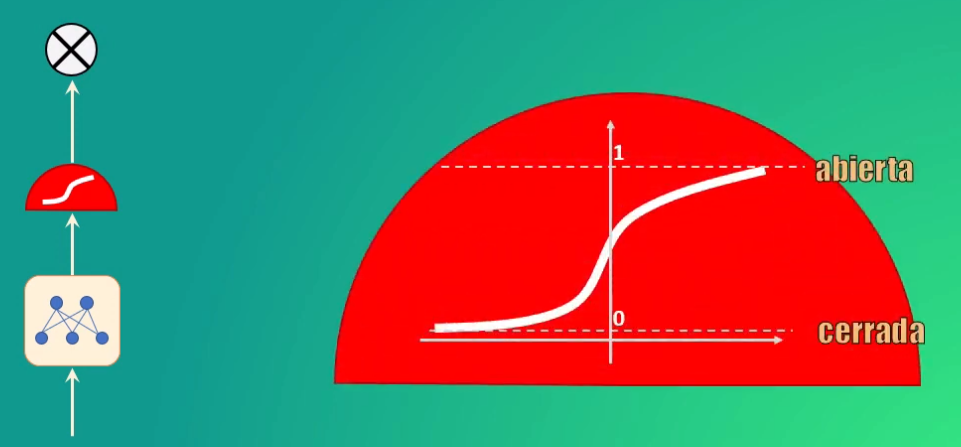
Veamos en detalle cómo el uso de las compuertas permite manipular la memoria de la celda LSTM
La compuerta forget permite decidir qué información se va a descartar, y que por tanto no pasará a la celda de estado.
Para ello toma el estado oculto anterior y la entrada actual, los transforma y los lleva a la función de activación sigmoidal. Los coeficientes (Ws y bs) se aprenden durante el entrenamiento, y como salida genera el vector f_t:
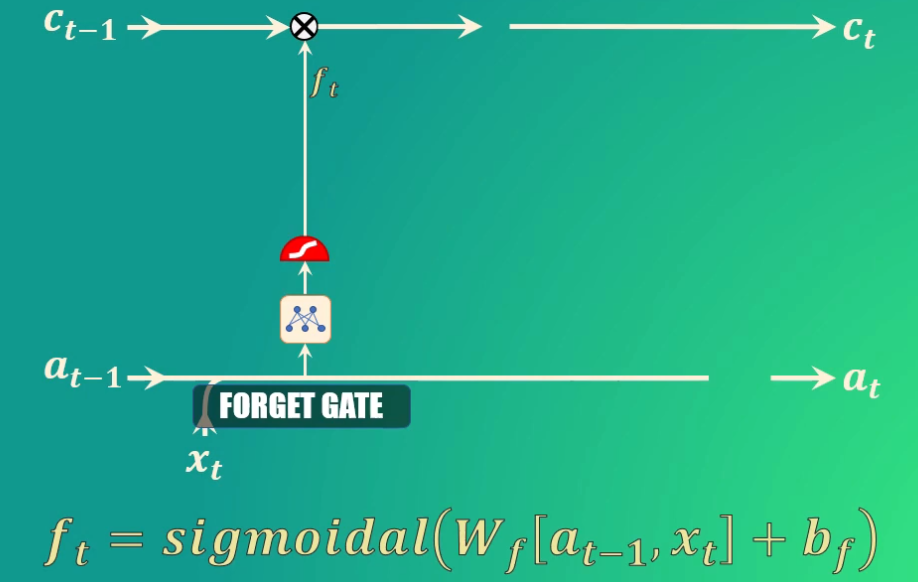
Si uno de los valores de este vector es 0 (o cercano a 0) entonces la LSTM eliminará esa porción de información, mientras que si alcanza valores iguales (o cercanos) a 1 esta información se mantendrá y llegará a la celda de estado.
Por ejemplo: si estamos analizando palabras dentro de un texto y entrenamos la LSTM para seguir la pista a variaciones gramaticales, podemos usar la red para detectar cambios en el sujeto de la oración, es decir si este es singular o plural.
Así, si inicialmente el sujeto es plural y luego dentro de la secuencia cambia a singular, podemos entrenar la forget gate para que detecte estas variaciones y elimine el sujeto plural, que deja de ser relevante. Bien, ya eliminamos el sujeto plural de la memoria de la red. ¿Y cómo agregamos el singular?
Para esto usamos la “update gate”, que como su nombre lo indica nos permite actualizar la memoria de la celda LSTM para indicar que ahora el sujeto es singular.
Para ello, tomamos nuevamente el estado oculto anterior y la entrada actual, los transformamos y los llevamos de nuevo a una función de activación sigmoidal. También en este caso, los coeficientes (Ws y bs) se aprenden durante el entrenamiento, y como salida esta compuerta genera el vector u_t:
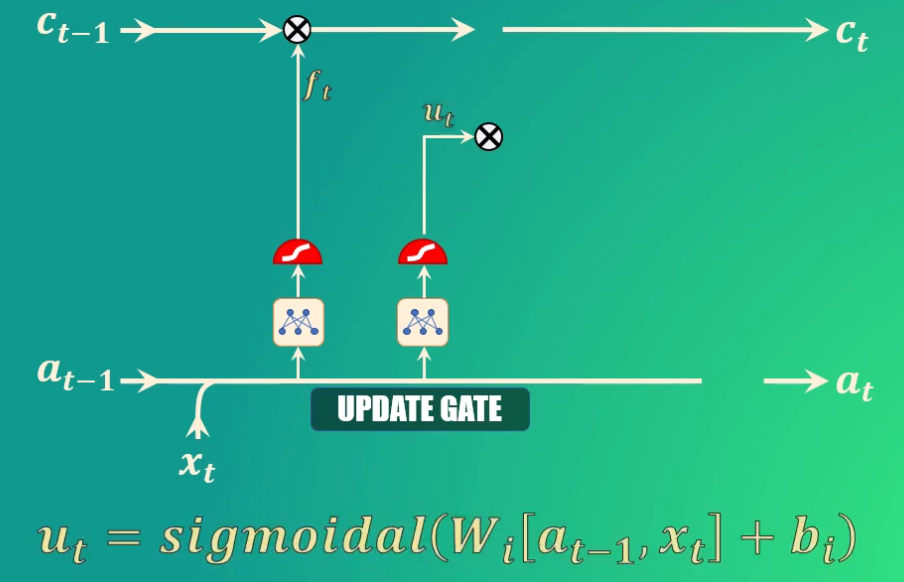
En este caso, los valores que queremos preservar en la memoria de la red serán aquellos cercanos a 1.
Teniendo ya los datos generados por las compuertas forget y update, podemos ahora sí actualizar la celda de estado (es decir la memoria de la red LSTM).
Actualización de la celda de estado
En primer lugar eliminamos la información irrelevante de la celda de estado, multiplicando el valor anterior de esta celda por el vector generado por la compuerta forget
A continuación creamos un vector de valores candidatos a formar parte de la nueva memoria. De nuevo, los parámetros Wc y bc se aprenden durante el entrenamiento
Ahora filtramos estos valores, multiplicando punto a punto el vector que acabamos de obtener con el generado por la compuerta “update”, y el resultado lo sumamos a los valores anteriores de la celda de estado, generando así la memoria actualizada:
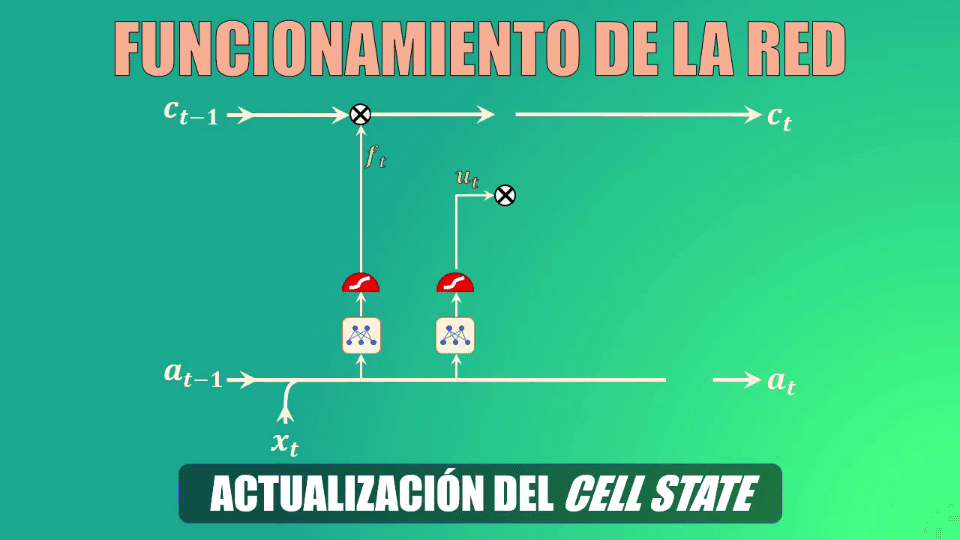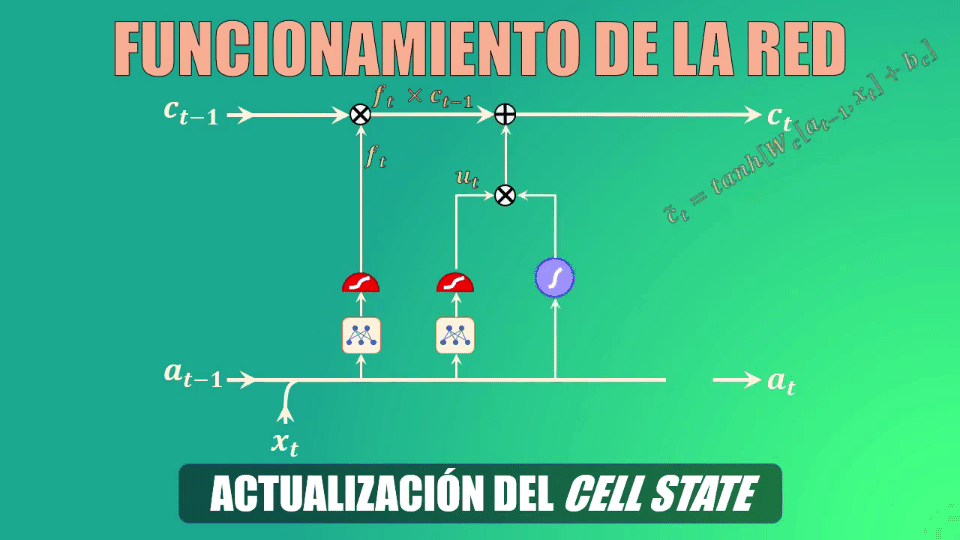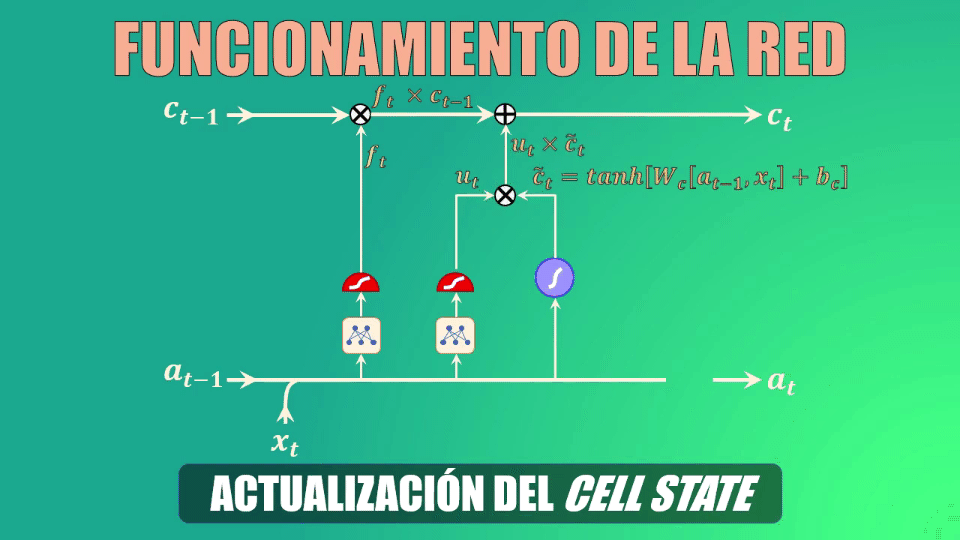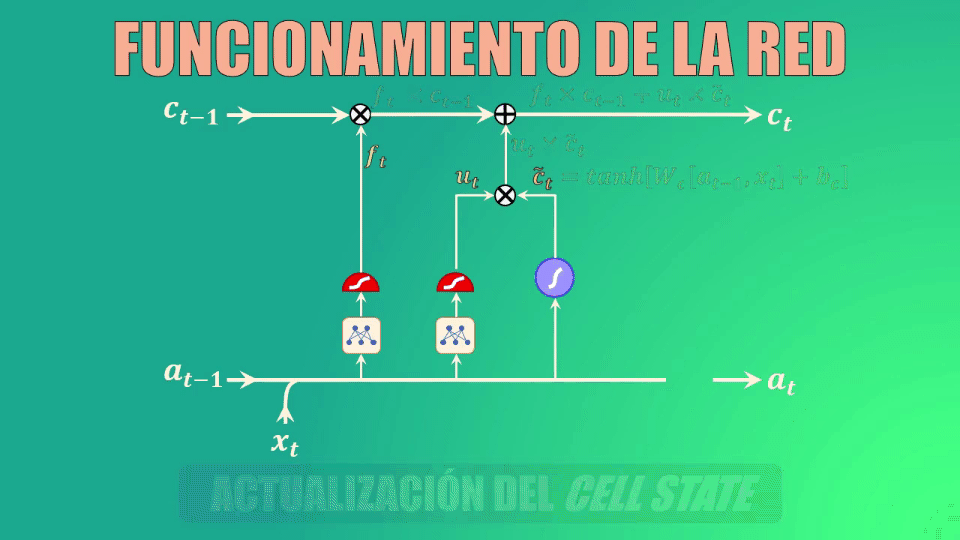
Cálculo del nuevo estado oculto
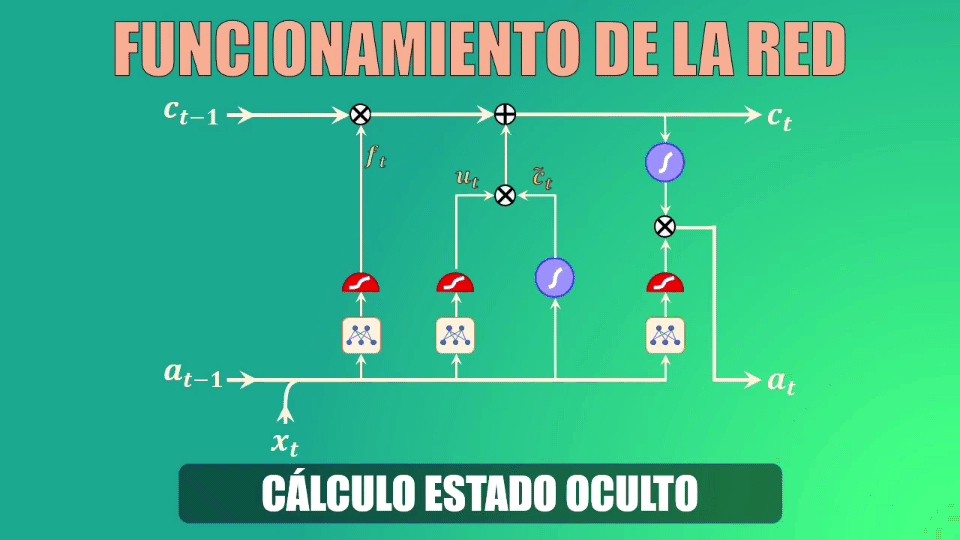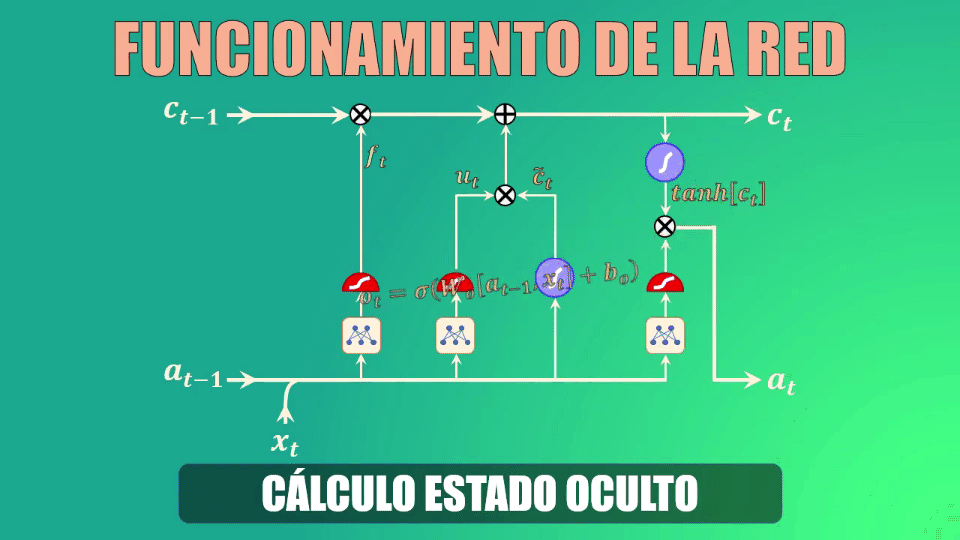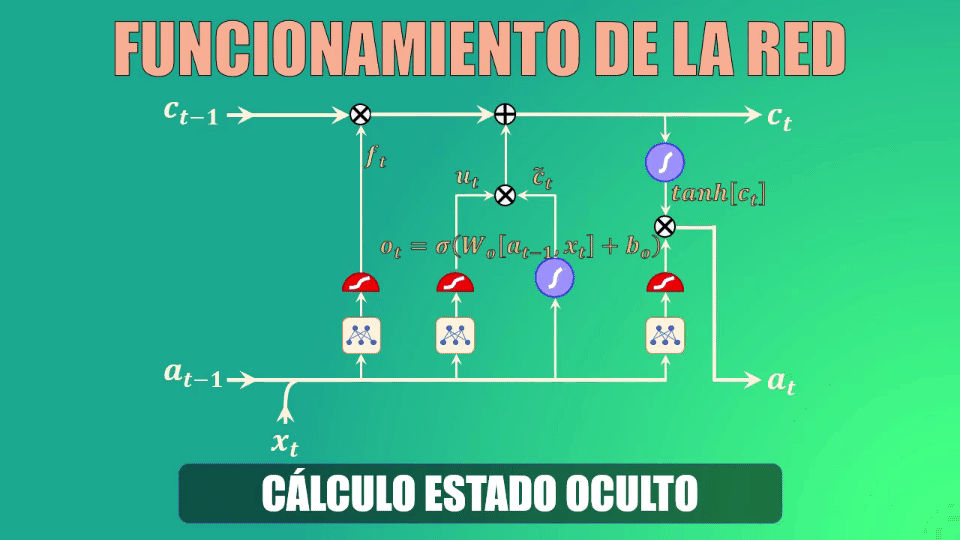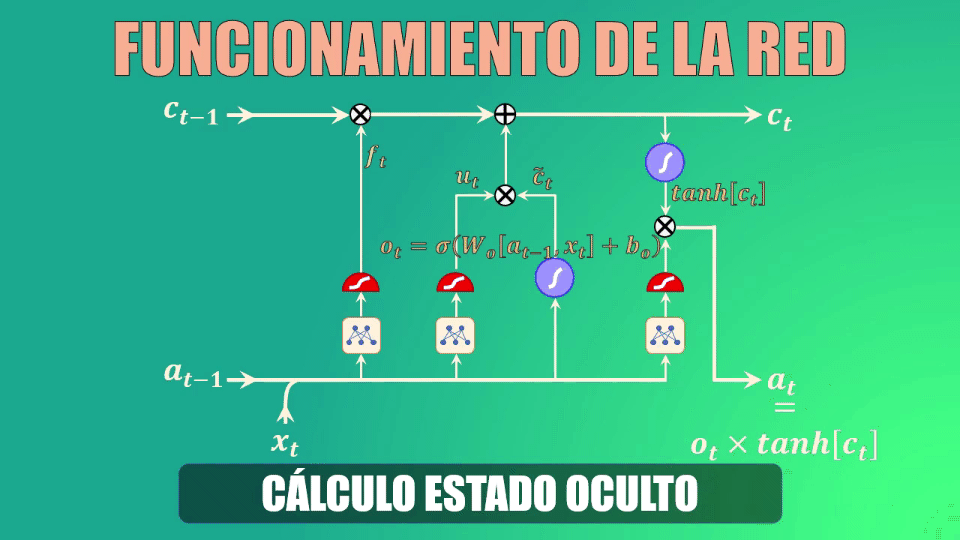
Finalmente debemos calcular el nuevo estado oculto, para lo cual usamos la output gate o compuerta de salida.
Este estado oculto de salida es simplemente una versión filtrada del estado de la celda que acabamos de generar.
En primer lugar escalamos el nuevo “cell state” para garantizar que esté en el rango de -1 a 1 (el rango que tiene precisamente el estado oculto). Para ello usamos la función tangente hiperbólica.
Ahora, usamos la compuerta de salida para determinar qué porciones del cell-state entrarán a formar parte del nuevo estado oculto. Al igual que en los casos anteriores, los parámetros Wo y bo serán aprendidos durante el entrenamiento.
Y finalmente, filtramos los valores del cell-state con el vector generado por la compuerta de salida:
Con esto ya tenemos todos los elementos que conforman una red LSTM.
Para finalizar veamos claramente cómo es que la red LSTM permite preservar la memoria, a diferencia de lo que ocurría con la red recurrente básica.
Ventaja de las Redes LSTM
Cuando analizamos una secuencia realmente tenemos réplicas de la celda LSTM vistas anteriormente, cada una de ellas correspondiente a un instante de tiempo diferente dentro de la secuencia.
Acá se evidencia claramente el concepto del cell state como “banda transportadora”: la información puede ser fácilmente removida o añadida de esta memoria: basta con entrenar adecuadamente las compuertas forget y update:
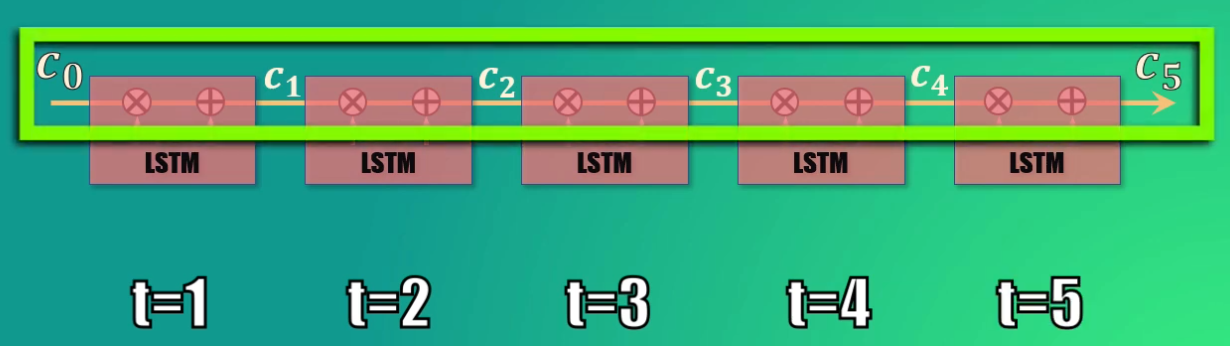
Así, es posible, con el entrenamiento adecuado, que la información almacenada en el estado C_0 se propague fácilmente hasta el estado C_5 o hasta estados posteriores, y que además la información irrelevante sea eliminada de la memoria en el momento adecuado.
Conclusión
Bien, en este post vimos en detalle cómo funciona una red LSTM, que es una versión mejorada de las Redes Neuronales Recurrentes básicas analizadas al comienzo de este curso.
Vimos que una Red Recurrente convencional tiene una memoria de corto plazo, resultado de las múltiples transformaciones que sufre el estado oculto a su paso por la red.
Las Redes LSTM resuelven este problema usando el concepto de la celda de estado (que es la memoria de la red). En estas Redes LSTM es posible agregar o eliminar información a esta celda de estado usando una serie de compuertas (forget, update y output) que permiten discriminar entre la información relevante e irrelevante.
Esto hace que las Redes LSTM sean mucho más robustas que las redes recurrentes convencionales, pues como su nombre lo indica poseen una memoria tanto de largo (long) como de corto (short) plazo.
Todo esto explica el auge que actualmente tienen las Redes LSTM para el desarrollo de diferentes aplicaciones, y son realmente la arquitectura a usar cuando hablamos de Redes Neuronales Recurrentes.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: