Redes Neuronales Recurrentes: Explicación Detallada
En este segundo post de la serie “Redes Neuronales Recurrentes” veremos en detalle cómo están conformadas internamente y cómo funcionan estas redes. Les explicaré en detalle los conceptos de activación y estado oculto, que son los elementos que permiten a las Redes Neuronales Recurrentes tener memoria y poder así procesar secuencias (como texto, audio y video, entre otras).
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
En el primer post de esta serie vimos una introducción general a las Redes Neuronales Recurrentes, una de las arquitecturas más usadas en el Machine Learning.
Vimos por ejemplo cómo las Redes Recurrentes permiten analizar secuencias (como conversaciones, videos o texto), haciendo uso de un concepto llamado “recurrencia” (que le da precisamente el nombre a estas redes).
En este post veremos en detalle cómo está conformadan conformadas internamente y cómo funcionan en detalle estas Redes Neuronales Recurrentes.
Para entender esto partamos de un problema hipotético: supongamos que queremos crear un modelo que sea capaz de generar nombres de dinosaurios.
La idea es entrenar el modelo con un listado de nombres de dinosaurios. Una vez realizado el entrenamiento, el modelo debería aprender a generar nuevos nombres, caracter por caracter.
En primer lugar, veamos porqué una Red Neuronal convencional o una Red Convolucional no están en capacidad de llevar a cabo esta tarea.
Limitaciones de las Redes Neuronales y Convolucionales
En las redes neuronales y convolucionales la información circula sólo en una dirección: desde la entrada hacia la salida, lo que las hace ideales para el reconocimiento de patrones (es decir, por ejemplo, para clasificar datos o imágenes):
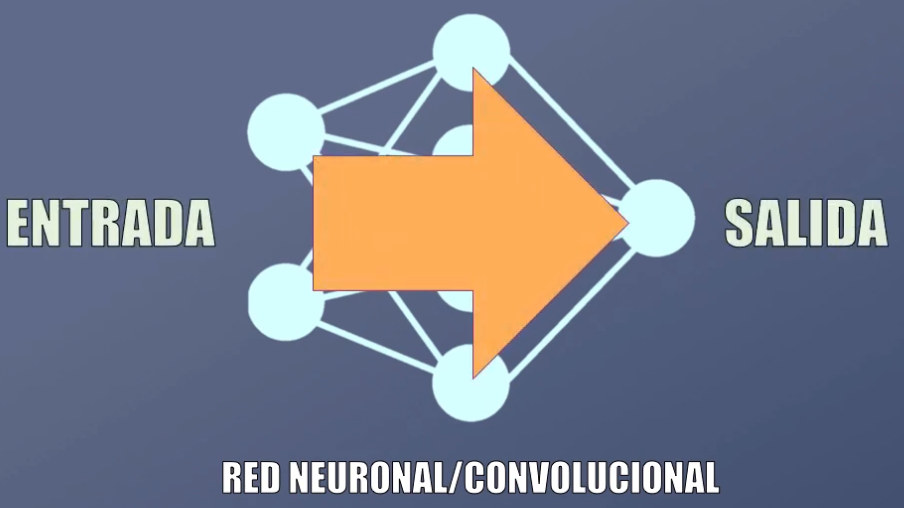
Si por ejemplo a una Red Convolucional ya entrenada le presentamos primero una imagen de un gato, ¡esto no implica que la red determinará que la siguiente imagen clasificada será un elefante!
Lo anterior quiere decir que las Redes Neuronales y Convolucionales sufren de amnesia: para generar una salida sólo consideran la entrada actual, no entradas pasadas o futuras.
Esta es la principal limitación de este tipo de redes, pues cuando hablamos de secuencias (como por ejemplo un texto, una conversación o un video) lo que nos interesa precisamente es que la red sea capaz de analizar el comportamiento de los datos en instantes previos (y posteriores) de tiempo.
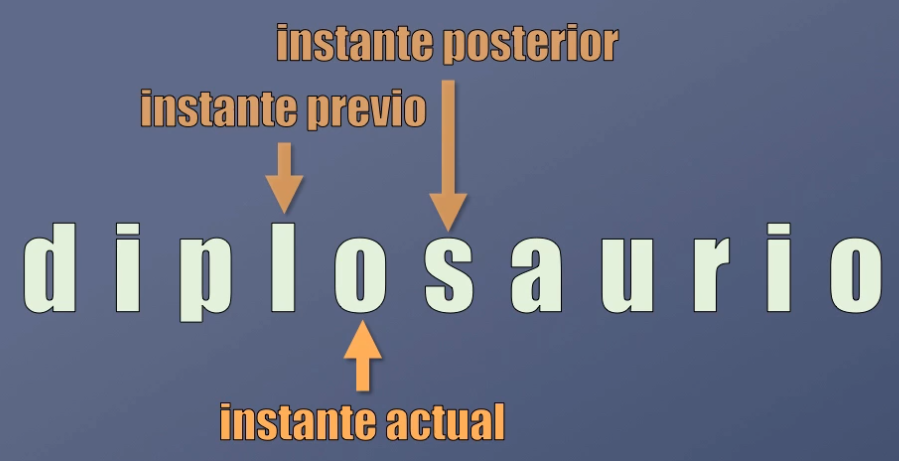
Así por ejemplo, en la palabra “diplosaurio” (un nombre ficticio de dinosaurio), para generar la letra “o” la red debería al menos tener en cuenta que el carácter “l” fue generado anteriormente:
Como vimos en el post anterior, las Redes Neuronales Recurrentes resuelven este inconveniente, pues para generar la salida tienen en cuenta no sólo lo que ocurre en el instante de tiempo actual sino la información proveniente de instantes de tiempo anteriores, lo que las hace ideales para analizar secuencias. Es decir que las redes recurrentes poseen un cierto tipo de memoria.
Veamos en detalle cómo es que logra hacer esto una Red Neuronal Recurrente.
Estructura de una Red Neuronal Recurrente
Notación
Comencemos por definir una notación básica.
En primer lugar definamos a qué nos referimos con instante de tiempo. Para una secuencia, el instante de tiempo es simplemente un número entero que define la posición de cada elemento dentro de la secuencia.
Así por ejemplo, en la palabra “d-i-p-l-o-s-a-u-r-i-o”, el instante de tiempo 1 corresponde al primer carácter de la secuencia (la letra “d”), el instante de tiempo 2 al segundo carácter (la letra “i”) y así sucesivamente:

Nos referiremos a $x_t$ como la entrada a la red recurrente en el instante de tiempo t, y a $y_t$ como la salida en el instante de tiempo t.
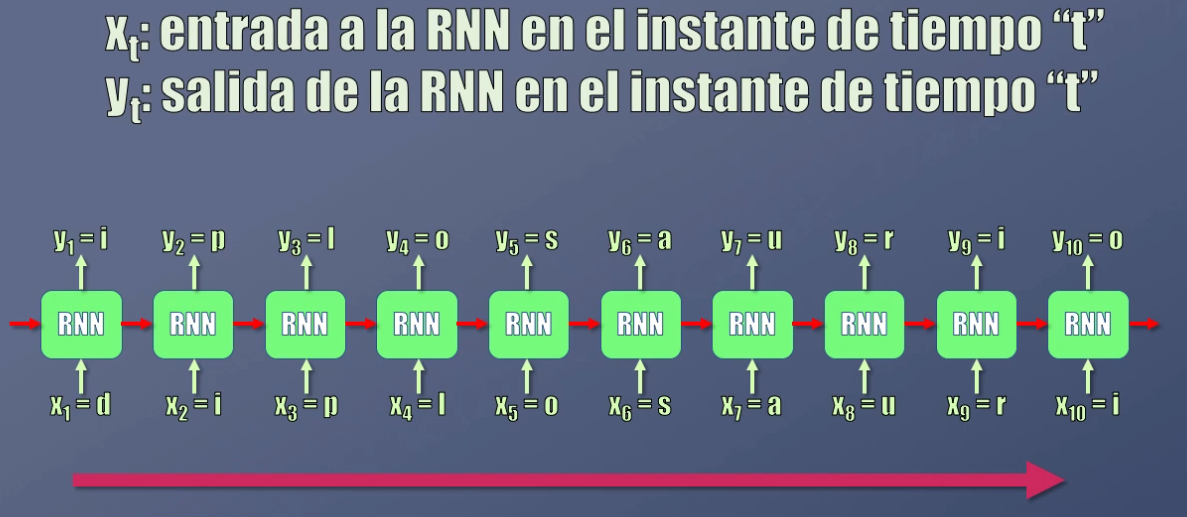
Es importante aclarar que en la figura vemos 10 bloques, pero la Red Recurrente es una sola. La idea de mostrar múltiples bloques es simplemente mostrar qué entradas y salidas se obtienen en diferentes instantes de tiempo.
La Red Recurrente: entradas y salidas
Pero, ¿cómo logra la Red Recurrente predecir correctamente el siguiente caracter en la secuencia? Es decir, ¿dónde está la memoria que mencionamos anteriormente?
La respuesta está precisamente en un elemento importante que observamos en la figura anterior: las flechas horizontales de color rojo. Se observa que en cada instante de tiempo la red tiene realmente dos entradas y dos salidas.
Las entradas son el dato actual ($x_t$) y la activación anterior ($a_{t-1}$), mientras que las salidas son la predicción actual ($y_t$) y la activación actual ($a_t$). Esta activación también recibe el nombre de “hidden state” o estado oculto:
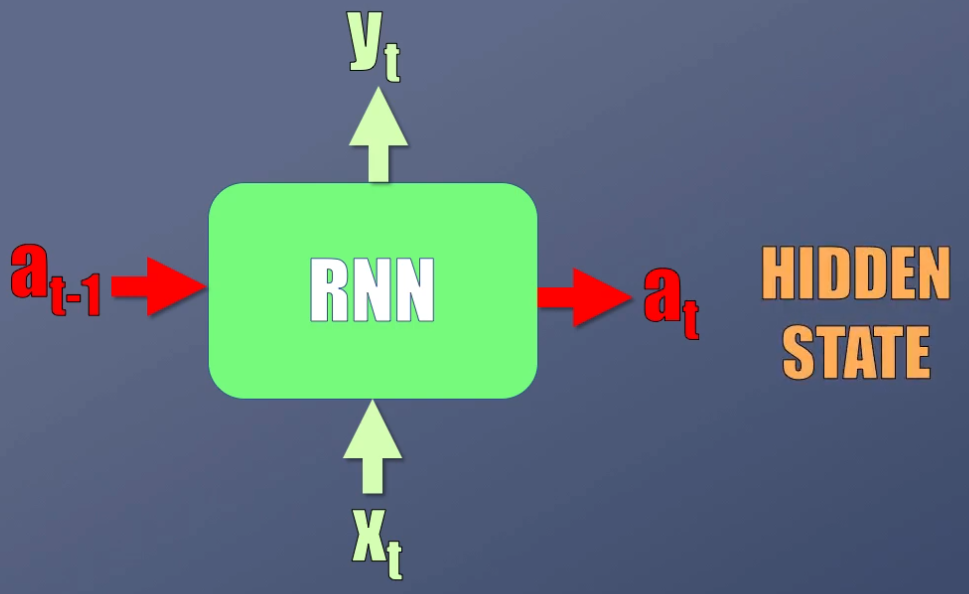
Son estas activaciones las que corresponden precisamente a la memoria de la red, pues permiten preservar y compartir la información entre un instante de tiempo y otro.
Veamos cómo se generan la predicción y la activación, y cómo estas se relacionan con la memoria de la red.
La Red Recurrente: funcionamiento detallado
Para calcular la salida y la activación de la Red Recurrente, a partir de sus dos entradas, se usa la misma lógica de una Neurona Artificial convencional.
En un post anterior vimos que esta Neurona Artificial tiene una entrada (x) y genera una salida (y), y que la salida es el resultado de aplicar dos operaciones al dato de entrada: una transformación y una función de activación no-lineal:
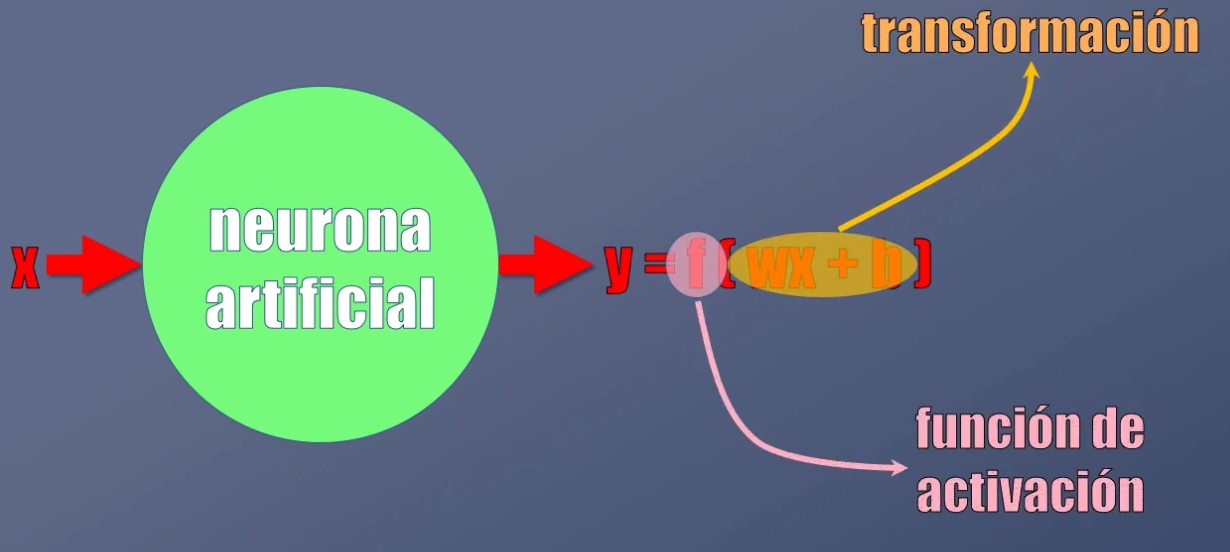
En el caso de las Redes Recurrentes, la activación se calcula de manera similar, y es el resultado primero de transformar los datos de entrada (es decir la activación anterior y la entrada actual) y luego llevarlos a una función de activación no-lineal:
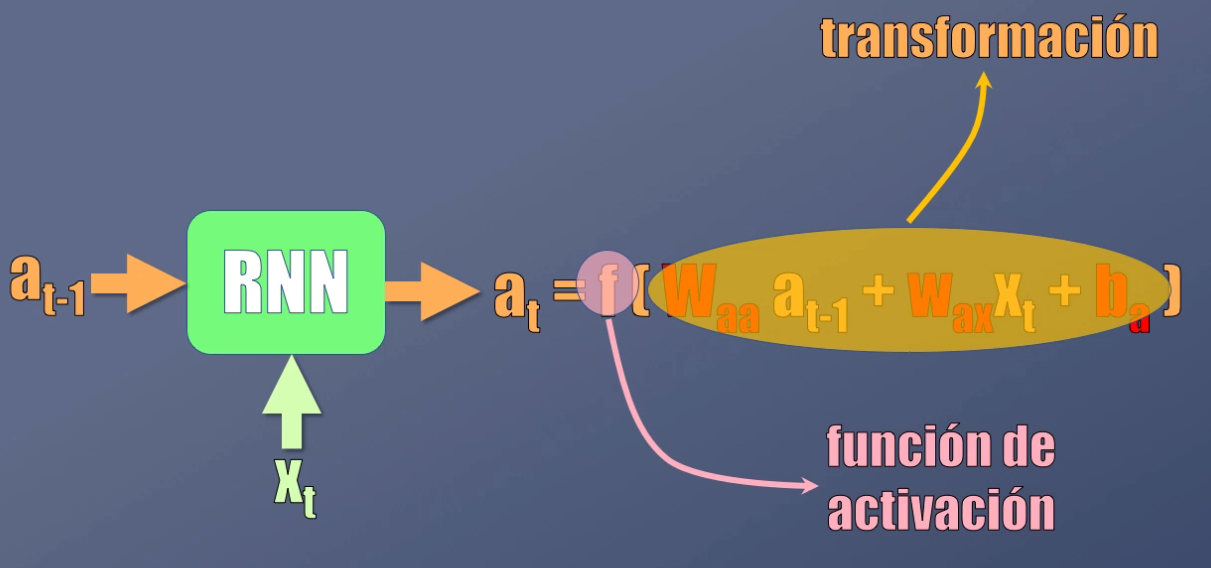
¿Y cómo se calculan los valores más adecuados de los coeficientes W y b? Con el mismo procedimiento usado en las Redes Neuronales, es decir a través del entrenamiento:

De igual forma, para obtener la salida, se usa la activación del instante previo y se realizan las mismas operaciones (transformación y función de activación) aplicadas anteriormente:

Al igual que en el caso anterior, los coeficientes W y b para el cálculo de esta salida se obtienen durante el proceso de entrenamiento.
Si observamos detalladamente estas dos ecuaciones, veremos el concepto de recurrencia y la memoria asociada a las redes recurrentes:
La salida $y_t$ depende de la activación actual ($a_t$) pero a su vez, dicha activación depende no solo de la entrada actual ($x_t$) sino igualmente del valor previo de la activación ($a_{t-1}$). ¡Esta es precisamente la memoria de la red! Y la forma como este concepto permite preservar y compartir la información entre uno y otro instante de tiempo:
Aclaración: representación extendida y compacta de las Redes Recurrentes
Para finalizar hagamos una aclaración importante. Volvamos al esquema mostrado originalmente para la Red Neuronal Recurrente:
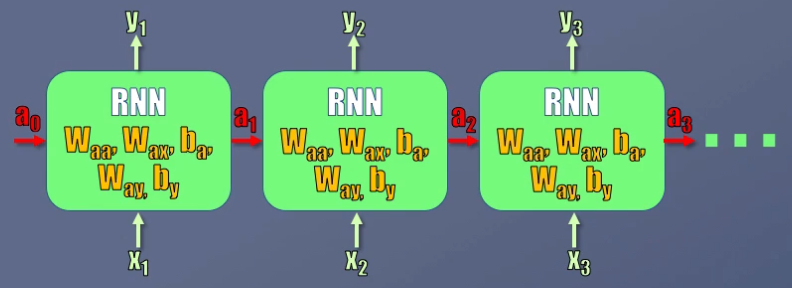
En este esquema se muestra el comportamiento de la red para tres instantes de tiempo diferentes. Sin embargo, es importante resaltar que la red es una sola, lo cual quiere decir que los coeficientes a calcular durante el entrenamiento serán los mismos entre uno y otro instante de tiempo.
La idea es que una vez entrenada la red recurrente sea capaz de generar la predicción usando el mismo set de parámetros en cada instante de tiempo.
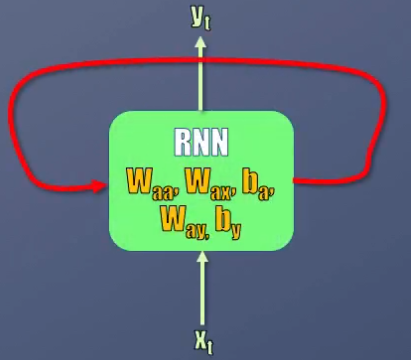
Es por eso que en ocasiones, en lugar de dibujar lo que sucede con la red en diferentes instantes de tiempo, se usa una representación compacta como la de la figura de abajo, en donde la flecha indica la dependencia entre la activación actual y la generada en un instante de tiempo anterior:
Conclusión
Bien, en este post vimos por qué las Redes Neuronales y Convolucionales no permiten analizar secuencias, y cómo las Redes Neuronales recurrentes resuelven este problema.
Para ello, la Red Recurrente tiene dos entradas: el dato actual y la predicción anterior. Al combinar estos dos elementos (usando una transformación y una función lineal, similares a las usadas en la Neurona Artificial vista anteriormente), es posible generar la salida de la red así como preservar la información obtenida en instantes de tiempo anteriores, lo que equivale precisamente a la memoria de la red.
En el siguiente post de esta serie veremos cómo aplicar todos estos conceptos en un ejemplo práctico en Keras, donde veremos paso a paso cómo generar texto usando una Red Neuronal Recurrente.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: