Tutorial: clasificación de imágenes con Redes Convolucionales en Python
En este cuarto post de la serie “Redes Convolucionales” veremos un tutorial para la clasificación de imágenes usando la Red Convolucional LeNet.
La Red Convolucional será capaz de determinar a qué número corresponde cada imagen, todo esto con muy pocas líneas de código y logrando una precisión cercana al 100%.
Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
En los tres primeros posts de esta serie vimos qué son las Redes Convolucionales, en qué consiste la convolución y qué son el padding, los strides, el max-pooling y el stacking.
En este tutorial veremos cómo combinar estas ideas para lograr clasificar imágenes usando Redes Convolucionales.
El tutorial está dividido en cuatro partes: primero veremos cuál es el set de datos, luego hablaremos de la Red Convolucional que usaremos, después veremos cómo implementarla en keras y finalmente analizaremos el desempeño de esta red.
Hablemos primero del set de datos.
El set de datos
El set que usaremos en este tutorial se llama MNIST, y contiene un total de 70,000 imágenes (60,000 de entrenamiento y 10,000 de validación), cada una de ellas en escala de gris y con un tamaño de 28x28.
Las imágenes contienen los dígitos del 0 al 9, escritos por diferentes personas:

El objetivo es implementar un clasificador capaz de determinar a qué digito corresponde cada imagen, independientemente de cómo este haya sido escrito.
Para ello usaremos LeNet, la arquitectura precursora de todas las redes convolucionales usadas en la actualidad. Veamos entonces en qué consiste esta red.
La Red Convolucional LeNet
La arquitectura de LeNet se muestra en la siguiente figura:
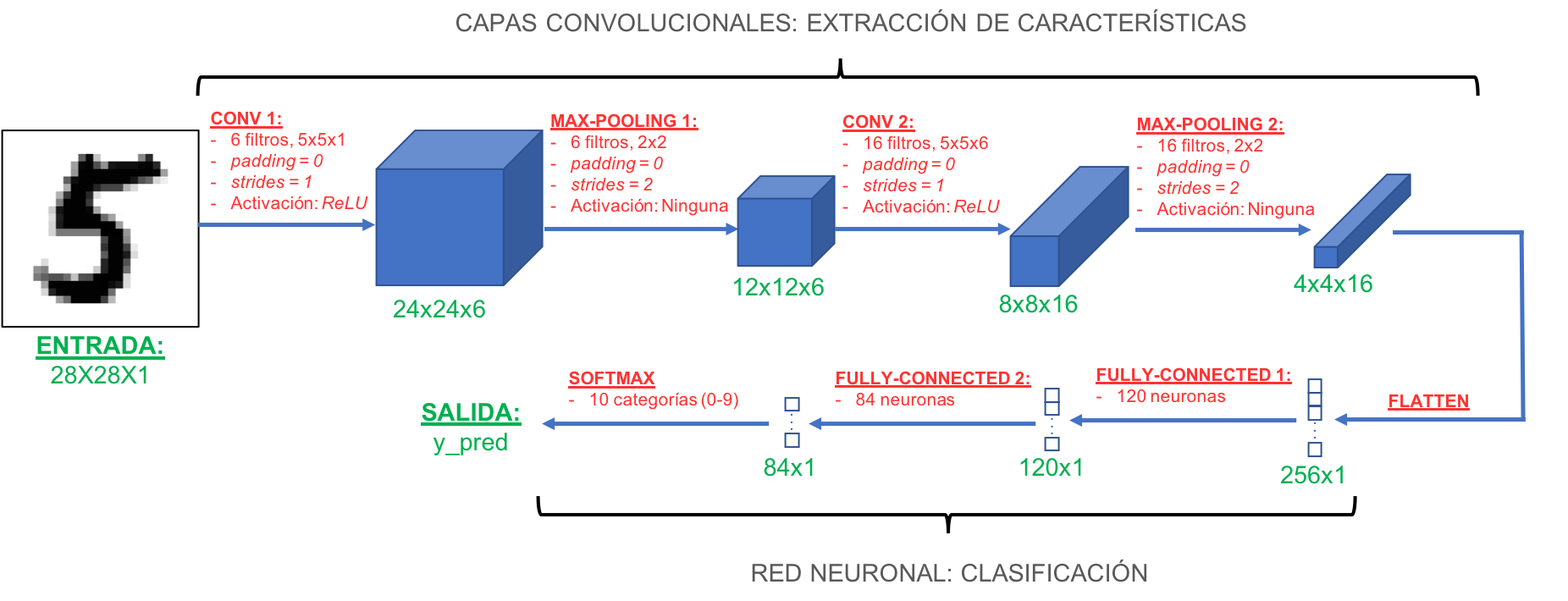
Veamos en detalle cada componente de esta red:
- La entrada a esta red es una imagen de 28x28, que contendrá un dígito escrito a mano.
- Posteriormente la red usa una serie de capas convolucionales y de max-pooling, para de manera progresiva extraer las características más relevantes de cada imagen. A medida que vamos más profundo en estas capas convolucionales, el ancho y alto de las imágenes resultantes va disminuyendo (pasando de 28x28 a 24x24, 12x12, 8x8 y 4x4) pero a la vez la profundidad de las mismas va en aumento (pasando de 1 a 6 y a 16). Esta profundidad indica precisamente que en las capas más ocultas se extraen más características de cada imagen.
- El objetivo del entrenamiento de esta red convolucional es precisamente entrenar los filtros CONV1 y CONV2 para que “aprendan” a extraer las características relevantes de cada una de las 60,000 imágenes de entrenamiento.
- La salida de las capas convolucionales es un volumen de 4x4x16, que contiene las características más relevantes de las imágenes de entrenamiento.
- En la etapa de salida, y para realizar la clasificación, se usa una pequeña Red Neuronal. Para ello primero se “aplana” el volumen de 4x4x16 de la etapa anterior, obteniendo así un vector de 256x1. Este es llevado a la Red Neuronal que tiene dos capas ocultas, la primera con 120 neuronas y la segunda con 84.
- Finalmente, la categoría a la que pertenece cada imagen es determinada por la capa de salida de esta red, que consiste en una función de activación softmax con 10 salidas (correspondientes a cada una de las posibles categorías, los dígitos del 0 al 9)
Implementación de la Red Convolucional en Python y Keras
Bien, ya tenemos una idea clara de en qué consiste esta red convolucional. Veamos ahora sí cómo implementarla.
Librerías requeridas
En primer lugar veamos qué librerías se deben importar.
Primero importamos Numpy y ajustamos la semilla del generador aleatorio, para tener reproducibilidad en el entrenamiento, es decir para que los coeficientes de los filtros y de la Red Neuronal se inicialicen siempre en el mismo valor aleatorio.
Además, importamos matplotlib para poder visualizar algunas imágenes del set de datos y los resultados del entrenamiento.
import numpy as np
np.random.seed(2)
import matplotlib.pyplot as plt
A continuación importamos la función mnist para cargar el set de datos de forma sencilla.
También importamos np_utils, que permite representar cada etiqueta de las imágenes en el formato one-hot, requerido por Keras durante el entrenamiento y la validación de la Red Convolucional:
from keras.datasets import mnist
from keras.utils import np_utils
Ahora, importamos las librerías Sequential (para crear el contenedor del modelo), Conv2D y Maxpooling2D (para implementar las capas convolucionales), Flatten y Dense (para la Red Neuronal) así como SGD (para usar el método del Gradiente Descendente durante el entrenamiento):
from keras.models import Sequential
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers.core import Flatten, Dense
from keras.optimizers import SGD
Lectura y pre-procesamiento de los datos
La lectura de los sets de entrenamiento y validación se realiza de forma sencilla usando la función mnist importada anteriormente:
(x_train, y_train), (x_test,y_test) = mnist.load_data()
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
Podemos verificar que efectivamente las imágenes tienen un tamaño de 28x28 y que los sets de entrenamiento contienen en total 60,000 y 10,000 imágenes:
(60000, 28, 28)
(60000,)
(10000, 28, 28)
(10000,)
Una vez leídos los datos, y antes de crear la Red Convolucional, es necesario reajustarlos para garantizar que el entrenamiento sea adecuado y para que los mismos tengan el formato requerido por Keras.
Primero normalizamos cada imagen, para que cada pixel esté en el rango de 0 a 1 (y no de 0 a 255). Esto es necesario para garantizar la convergencia del algoritmo del Gradiente Descendente durante el entrenamiento:
x_train = x_train/255.0
x_test = x_test/255.0
A continuación convertimos las etiquetas de los sets de entrenamiento y validación al formato one-hot, usando la función np_utils. En este formato, cada categoría estará representada con una secuencia de números binarios: por ejemplo los dígitos que pertenezcan a la categoría 4 serán representados por la secuencia $[0, 0, 0, 0, 1, 0, 0, 0, 0, 0]$ (de ahí el nombre one-hot: sólo uno de los dígitos será diferente de cero):
nclases = 10
y_train = np_utils.to_categorical(y_train,nclases)
y_test = np_utils.to_categorical(y_test,nclases)
Veamos cómo es una de las imágenes del set de entrenamiento. Para ello escogemos una imagen del set y, con Matplotlib, visualizamos la imagen y la categoría correspondiente:
nimagen = 100
plt.imshow(x_train[nimagen,:].reshape(28,28), cmap='gray_r')
plt.title('Imagen ejemplo - Categoría: ' + str(np.argmax(y_train[nimagen])))
plt.axis('off')
plt.show()
Finalmente, debemos reajustar las imágenes de entrenamiento y validación, para indicar explícitamente a Keras que cada imagen tendrá un solo canal de información (por tratarse de imágenes en escala de gris). Para esto usamos la función reshape de Numpy:
x_train = x_train.reshape(60000,28,28,1)
x_test = x_test.reshape(10000,28,28,1)
Creación del modelo en Keras
Bien, ya tenemos todo listo para implementar el modelo usando Keras.
En esta tabla vemos las características de cada capa:
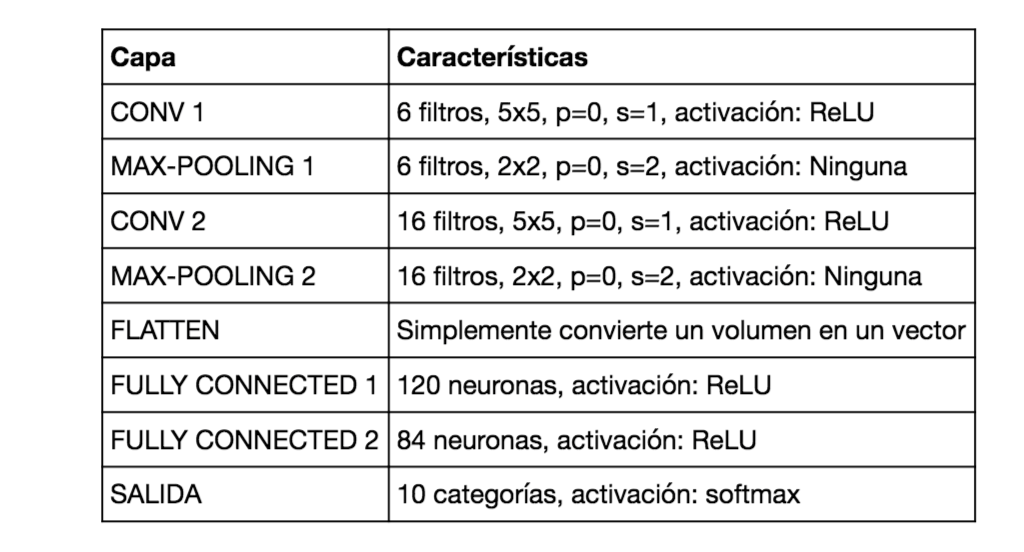
El primer paso es usar Sequential para crear el contenedor del modelo, en donde progresivamente se irán añadiendo las diferentes capas de la Red Convolucional:
modelo = Sequential()
Ahora añadimos la primera capa convolucional, con 6 filtros, cada uno de 5x5, sin padding y con stride igual a 1 y función de activación ReLU. Debemos igualmente definir de forma explícita el tamaño de cada imagen de entrada (28x28x1):
# CONV1 Y MAX-POOLING1
modelo.add(Conv2D(filters=6, kernel_size=(5,5), activation='relu', input_shape=(28,28,1)))
Vemos que el uso de Conv2D no requiere en este caso que definamos el padding ni los strides de forma explícita. Por defecto, Keras usará un padding igual a 0 y un stride igual a 1.
Ahora, añadimos la primera capa max-pooling. En este caso se usan 6 filtros (los mismos de la capa anterior) y no se usa padding. De nuevo, en Keras basta con definir únicamente el tamaño de cada filtro usando la palabra clave pool_size, los demás parámetros (padding = 0 y strides = 2 no se deben introducir explícitamente en la función):
modelo.add(MaxPooling2D(pool_size=(2,2)))
La segunda capa convolucional y la segunda de max-pooling se crean de la misma forma que las anteriores, con la única diferencia que en este caso el número de filtros es igual a 16:
# CONV2 Y MAX-POOLING2
modelo.add(Conv2D(filters=16, kernel_size=(5,5), activation='relu'))
modelo.add(MaxPooling2D(pool_size=(2,2)))
Finalmente, aplanamos el volumen resultante usando Flatten() y creamos la Red Neuronal con 120 neuronas en la primera capa, 84 en la segunda y una salida tipo softmax con 10 categorías.:
# Aplanar, FC1, FC2 y salida
modelo.add(Flatten())
modelo.add(Dense(120,activation='relu'))
modelo.add(Dense(84,activation='relu'))
modelo.add(Dense(nclases,activation='softmax'))
Compilación del modelo
En este paso definimos el optimizador, es decir el método que se usará para actualizar los coeficientes de los filtros y de la Red Neuronal durante el entrenamiento.
En nuestro caso usaremos el método del Gradiente Descendente, y fijaremos una tasa de aprendizaje de 0.1:
sgd = SGD(lr=0.1)
Ahora asociamos este optimizador al modelo creado previamente, y además definimos nuestra función de error y la métrica con la que evaluaremos el desempeño de la red convolucional. Para esto hacemos uso de la función compile.
Por tener un total de 10 categorías de salida, haremos uso de la “entropía cruzada” (categorical_crossentropy) como función de error, mientras que el desempeño de la red será evaluado usando la “precisión” (accuracy) definida como número de aciertos sobre el número total de datos en los sets de entrenamiento y validación:
modelo.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
Entrenamiento y validación del modelo
Ahora sí está todo listo para hacer el entrenamiento.
Usaremos un total de 10 iteraciones y, por ser un set de 60,000, en cada iteración del entrenamiento lo dividiremos en bloques de 128 imágenes (para no tener problemas con el almacenamiento de los datos en memoria).
Para el entrenamiento usamos la función fit y podemos usar la palabra clave validation_data para que durante el mismo entrenamiento Keras evalúe la precisión que se logra con el set de validación. De todos modos es importante tener en cuenta que este set de validación se usa sólo para medir el desempeño del modelo, pero no para entrenarlo ni para aprender los coeficientes (para ello se usa el set de entrenamiento):
nepochs = 10
tam_lote = 128
modelo.fit(x_train,y_train,epochs=nepochs,batch_size=tam_lote, verbose=1, validation_data=(x_test,y_test))
Vemos que al finalizar el entrenamiento se alcanza una precisión de más del 99% con el set de entrenamiento, y superior al 98% con el set de validación:
Train on 60000 samples, validate on 10000 samples
Epoch 1/10
60000/60000 [==============================] - 21s 345us/step - loss: 0.3510 - acc: 0.8878 - val_loss: 0.0973 - val_acc: 0.9705
Epoch 2/10
60000/60000 [==============================] - 20s 338us/step - loss: 0.0881 - acc: 0.9726 - val_loss: 0.0787 - val_acc: 0.9745
Epoch 3/10
60000/60000 [==============================] - 20s 331us/step - loss: 0.0631 - acc: 0.9802 - val_loss: 0.0597 - val_acc: 0.9816
Epoch 4/10
60000/60000 [==============================] - 20s 328us/step - loss: 0.0505 - acc: 0.9841 - val_loss: 0.0812 - val_acc: 0.9751
Epoch 5/10
60000/60000 [==============================] - 19s 316us/step - loss: 0.0430 - acc: 0.9865 - val_loss: 0.0439 - val_acc: 0.9859
Epoch 6/10
60000/60000 [==============================] - 20s 334us/step - loss: 0.0374 - acc: 0.9881 - val_loss: 0.0388 - val_acc: 0.9877
Epoch 7/10
60000/60000 [==============================] - 20s 326us/step - loss: 0.0327 - acc: 0.9898 - val_loss: 0.0395 - val_acc: 0.9875
Epoch 8/10
60000/60000 [==============================] - 20s 328us/step - loss: 0.0280 - acc: 0.9913 - val_loss: 0.0393 - val_acc: 0.9878
Epoch 9/10
60000/60000 [==============================] - 20s 334us/step - loss: 0.0244 - acc: 0.9926 - val_loss: 0.0348 - val_acc: 0.9894
Epoch 10/10
60000/60000 [==============================] - 20s 336us/step - loss: 0.0225 - acc: 0.9930 - val_loss: 0.0431 - val_acc: 0.9864
Bien, acabamos de ver que el modelo entrenado tiene un desempeño bastante bueno, pues la precisión con el set de validación (es decir, con datos que no ha visto previamente) es prácticamente del 99%. Lo anterior quiere decir que de cada 100 datos, en promedio el modelo clasifica incorrectamente tan sólo 1. ¡Lo cual no está nada mal para esta Red Convolucional!
Para finalizar, veamos cómo analizar el desempeño del modelo de forma más detallada usando algo que se conoce como la matriz de confusión.
Análisis detallado del desempeño del modelo: la matriz de confusión
La precisión que obtuvimos anteriormente es una medida global del desempeño de esta Red Convolucional, pero no nos permite ver si algunos dígitos son clasificados con mayor precisión que otros.
Para poder ver este desempeño detalladamente usamos la matriz de confusión, que en este caso será una matriz de 10 filas por 10 columnas, en donde las filas indican la categoría a la que realmente pertenecen las imágenes, mientras que las columnas corresponden a la predicción realizada por el modelo.
Para obtener esta matriz primero importamos la función “graficar_matriz_de_confusion”. No veremos en detalle esta función, pero podrás encontrarla en el código fuente de este tutorial (el enlace se encuentra al final del artículo):
from matriz_confusion import graficar_matriz_de_confusion
La predicción realizada por el modelo la obtenemos usando la función predict_classes, mientras que la categoría real corresponde al arreglo y_test cargado inicialmente:
y_pred = modelo.predict_classes(x_test)
Finalmente, graficamos la matriz de predicción:
y_ref = np.argmax(y_test,axis=1)
etiquetas = ['0','1','2','3','4','5','6','7','8','9']
graficar_matriz_de_confusion(y_ref, y_pred, etiquetas)
con lo que obtenemos la siguiente matriz de confusión:
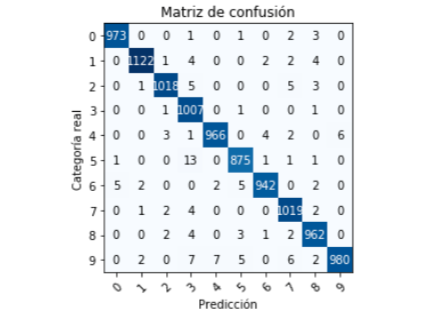
¿Y cómo se interpreta esta matriz de confusión? Si tuviéramos un clasificador ideal (precisión del 100%), todos los números diferentes de cero deberían estar en la diagonal principal.
Sin embargo, vemos que a pesar de que la precisión es muy alta, el clasificador no es ideal (¡en realidad ningún clasificador lo es!).
Veamos dos casos extremos: ¿para cuál de los dígitos se logra la peor precisión y para cual la mejor durante la clasificación?
La precisión más baja se obtiene con el número 5. En la matriz de confusión vemos que fue clasificado correctamente 875 veces. Pero este mismo dígito fue clasificado incorrectamente como el número 3 un total de 13 veces, y que una vez fue clasificado incorrectamente como 0, 6, 7 u 8. Esto quiere decir que para este dígito en particular se alcanza una precisión del 98%.
Por otra parte, la precisión más alta se obtiene con el número 3, que fue clasificado correctamente 1007 veces, e incorrectamente tan solo 3, lo que nos da una precisión del 99.7%.
Conclusión
Bien, en este tutorial vimos cómo clasificar imágenes usando Redes Convolucionales y la librería Keras. Al clasificar los digitos, logramos una precisión cercana al 99%. Para ello hemos usado LeNet, la arquitectura precursora de las redes convolucionales actuales.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:
Datos y código fuente
En este enlace de Github podrás descargar el código fuente de este tutorial.