Tutorial Python: ¿Cómo combatir el Overfitting en el Machine Learning?

Octubre 1, 2019 por Miguel Sotaquirá

En este tutorial veremos tres de las técnicas más usadas para combatir el Overfitting en el Machine Learning: (1) usar modelos más simples, (2) el Dropout y (3) el early stopping.

En un post anterior hablamos del overfitting y el underfitting, dos conceptos que están asociados al desempeño de un modelo de Machine o de Deep Learning.

En este tutorial nos enfocaremos en el Overfitting, que recordemos se produce cuando el modelo funciona bastante bien con el set de entrenamiento pero tiene un desempeño pobre con el set de validación.

A través de un ejemplo práctico en Keras, veremos tres de las técnicas más usadas para combatir este problema

Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.

Así que, ¡listo, comencemos!

Tabla de contenido

Video

Como siempre, en el canal de YouTube se encuentra el video de este post:

Lectura y pre-procesamiento del set de datos

Hablemos primero del set de datos que usaremos en este tutorial.

Este contiene variables fisiológicas con las que se intenta predecir si una persona puede desarrollar diabetes en un futuro. Por cada sujeto se tienen, entre otras, variables como el número de embarazos que ha tenido, la concentración de glucosa en la sangre o el índice de masa corporal. En total son 8 características y 768 sujetos:

Generalidades del set de datos que contiene 768 sujetos, cada uno definido por 8 características

Adicionalmente, por cada sujeto se define la categoría a la que pertenece: 1: positivo o 0 negativo para diabetes.

Para leer este set usamos inicialmente Numpy, y creamos los arreglos $X$ y $Y$ que contendrán respectivamente las características y la categoría a la que pertenece cada sujeto:

import numpy as np

dataset = np.loadtxt("dataset.csv", delimiter=",")
X = dataset[:, 0:8]
Y = dataset[:, 8]

En primer lugar debemos normalizar los datos ($X$), para garantizar que todas las características estén en la misma escala. Para ello usamos el módulo StandardScaler de la librería Scikit-Learn:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
X = scaler.transform(X)

Una vez normalizados los datos, creamos los sets de entrenamiento y de validación, que tendrán una proporción del 80 y 20% respectivamente. De nuevo usamos Scikit-Learn y el módulo train_test_split, en donde sólo basta con definir el tamaño del set de validación (20%, o 0.2):

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

y donde hemos usado random_state=42 en la anterior línea de código para garantizar que la semilla del generador aleatorio siempre es la misma y por tanto la partición de los dos sets (entrenamiento y validación) siempre contendrá los mismos datos cada vez que ejecutemos el código.

Modelo base

Creemos un primer modelo base (o de referencia) para clasificar estos datos, donde intencionalmente usaremos más capas y neuronas de las necesarias para hacer que el modelo presente Overfitting. Este modelo será el referente para las próximas secciones, en donde implementaremos ligeros cambios para reducir este Overfitting.

El modelo será una simple Red Neuronal con dos capas ocultas: la primera contendrá 1000 neuronas y la segunda 250, ambas con función de activación ReLU, mientras que la capa de salida (que indicará la categoría a la que pertenece el dato), tendrá una sola neurona y función de activación sigmoidal:

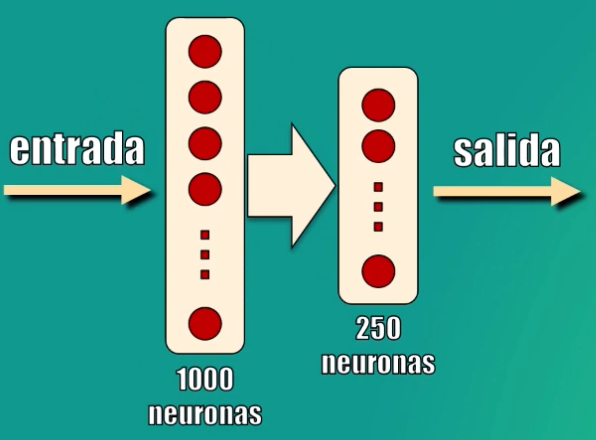
El modelo de referencia que usaremos en este tutorial

Creación del modelo en Keras

Para crear este modelo usaremos los módulos Sequential y Dense de Keras:

np.random.seed(100)

model = Sequential()
model.add(Dense(1000, input_dim=8, activation='relu'))
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

En este caso hemos usado np.random.seed(100) para fijar la semilla del generador aleatorio y garantizar así la reproducibilidad del entrenamiento cada vez que ejecutemos el código.

Entrenamiento del modelo

Para el entrenamiento usaremos la entropía cruzada, que es la misma función usada en la Regresión Logística, para lo cual usaremos el optimizador adam que, de forma similar a como lo hace el algoritmo del Gradiente Descendente, permite de forma iterativa minimizar la función de error (es decir la entropía cruzada). Por su parte la métrica de desempeño (que evaluará qué tan bien realiza la clasificación el modelo) será la precisión (accuracy):

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

Entrenaremos el modelo con el método fit, presentaremos bloques de 64 ejemplos de entrenamiento (batch_size=64) por un total de 150 iteraciones (epochs=150). De manera simultánea realizaremos la validación (validation_data=(x_test,y_test)) para de esta forma ver cómo evolucionan tanto el error como la precisión con ambos sets durante el entrenamiento:

historia = model.fit(x_train, y_train, batch_size=64, epochs=150, validation_data=(x_test,y_test), verbose=1)

Resultado del entrenamiento: overfitting

Una vez realizado el entrenamiento podemos observar el comportamiento del error y de la precisión:

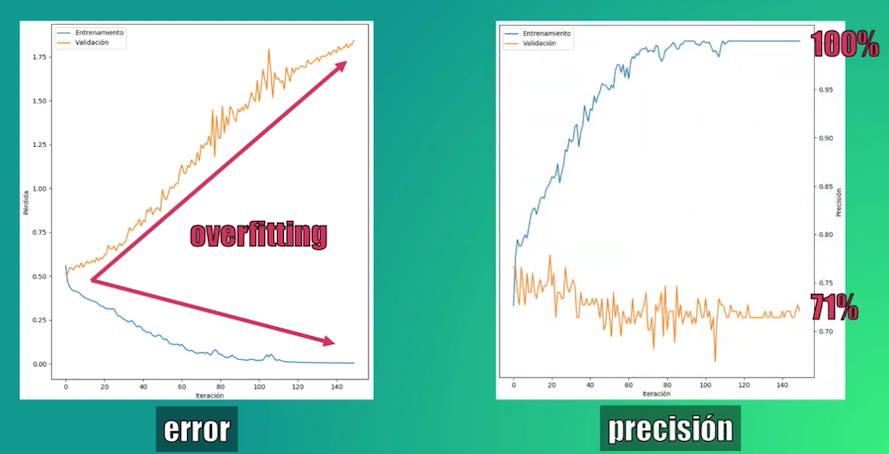
Resultado del entrenamiento del modelo de referencia, en donde se observa la presencia de overfitting

En el caso del set de entrenamiento el error se reduce progresivamente. Sin embargo, con el set de validación el error se incrementa progresivamente! Esto es una señal clara de Overfitting, lo que se puede comprobar al verificar la precisión: 100% con el set de entrenamiento y tan sólo 71% con el de validación.

¿Y a qué se debe este overfitting? En este caso hay dos razones:

Tenemos realmente muy pocos datos (tan solo 768 en total) y cada uno de ellos tiene sólo 8 características,
Sin embargo, la Red Neuronal tiene demasiadas neuronas y capas ocultas, pues en total tiene casi 260 mil parámetros. Es un modelo que resulta excesivamente complejo para el set de datos que se quiere analizar.

Veamos entonces tres técnicas para reducir este Overfitting.

Tres técnicas para reducir el overfitting

Simplificar el modelo

La primer técnica para combatir el overfitting es la más intuitiva: si el modelo es demasiado complejo, la solución consiste simplemente en reducir el número de capas y/o el número de neuronas en cada capa.

Así que diseñaremos un segundo modelo que será una Red Neuronal con tan sólo una capa oculta con 100 neuronas, adicional a las capas de entrada y de salida originales del modelo base:

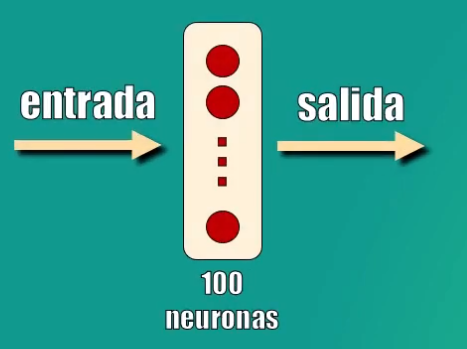
Red Neuronal simplificada, con una capa oculta con 100 neuronas y las capas de entrada y salida originales

Este modelo lo creamos y entrenamos de manera similar a como lo hicimos con el modelo de referencia, usando los módulos Sequential y Dense de Keras:

model = Sequential()
model.add(Dense(100, input_dim=8, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
historia = model.fit(x_train, y_train, batch_size=64, epochs=150, validation_data=(x_test,y_test), verbose=1)

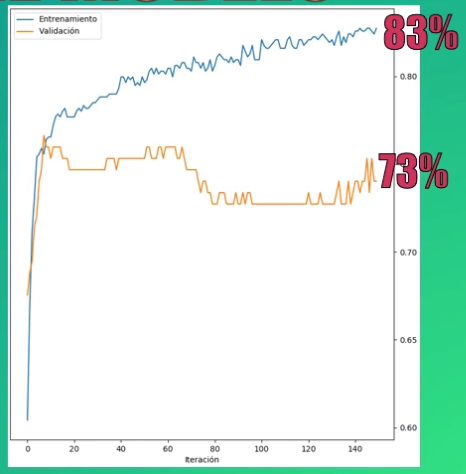
Al entrenar el modelo y validarlo, vemos que se ha sacrificado la precisión del set de entrenamiento (pues ahora bajó a aproximadamente el 83%), pero se ha incrementado la del set de validación (pasando de 71 a 73%), reduciendo así el overfitting:

Comportamiento de la precisión para los sets de entrenamiento y validación del modelo simplificado

El Dropout

Veamos la segunda técnica, el Dropout, que en la actualidad es una de las más usadas para reducir el overfitting.

Esta técnica es muy sencilla, consiste simplemente en “apagar”, para cada una de las capas, un porcentaje de las neuronas para que no sean entrenadas, evitando así que sus coeficientes se modifiquen. En cada iteración las neuronas inactivas son seleccionadas de forma aleatoria durante el algoritmo, con lo que se logra mejorar la capacidad de generalización del modelo:

En Keras es muy sencillo implementar el Dropout. Basta con agregar esta función a la salida de cada capa del modelo original, especificando el porcentaje de neuronas que estarán inactivas:

model = Sequential()
model.add(Dense(1000, input_dim=8, activation='relu'))
model.add(Dropout(0.9))
model.add(Dense(250, activation='relu'))
model.add(Dropout(0.8))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
historia = model.fit(x_train, y_train, batch_size=64, epochs=150, validation_data=(x_test,y_test), verbose=1)

En las líneas de código anteriores, se usaron valores de Dropout correspondientes al 90% (model.add(Dropout(0.9))) y al 80% (model.add(Dropout(0.8))) en cada una de las capas del modelo base inicial.

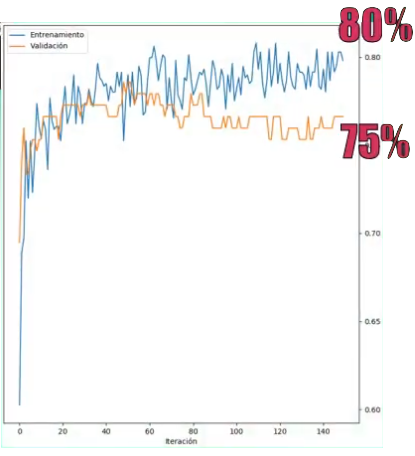
Al entrenar el modelo se observa un incremento en la precisión del set de validación, llegando al 75%:

Comportamiento de la precisión para los sets de entrenamiento y validación del modelo con Dropout

Early stopping

Finalmente, la tercera técnica se conoce como Early stopping.

Si volvemos al modelo entrenado con Dropout, observamos que el error de validación comienza a incrementarse después la iteración 10, aproximadamente:

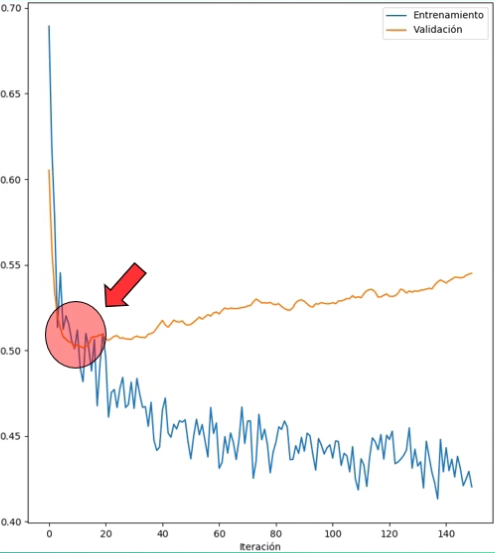
Después de la iteración 10 el error de validación comienza a incrementarse. Es en este punto donde se puede detener el entrenamiento del modelo, lo que se conoce como 'early stopping'

La idea del Early stopping es sencilla: detener el entrenamiento en el momento que se observe un incremento en el valor del error de validación. Al hacer esto se logra entrenar el modelo para que este error sea mínimo y, por tanto, su precisión sea máxima, reduciendo así el overfitting.

Así que tomaremos el modelo Dropout y agregaremos early stopping durante el entrenamiento.

Esto es sencillo en Keras: creamos un callback con la función EarlyStopping, especificando que vamos a seguir el comportamiento del error de validación, y que después de observar el valor mínimo esperaremos cuatro iteraciones, y si este valor no se reduce detendremos el entrenamiento:

early_stop = EarlyStopping(monitor='val_loss', patience=4, restore_best_weights=True)
historia = model.fit(x_train, y_train, batch_size=64, epochs=150, validation_data=(x_test,y_test), verbose=1, callbacks=[early_stop])

Con la palabra clave restore_best_weights le indicamos a Keras que use los coeficientes de entrenamiento obtenidos en el punto mínimo alcanzado por el error.

Al usar el early stopping vemos que el entrenamiento se detiene tras 13 iteraciones. Sin embargo es en la iteración 9 en donde el error es mínimo, y por tanto los coeficientes finales del modelo corresponderán a los calculados en esta iteración:

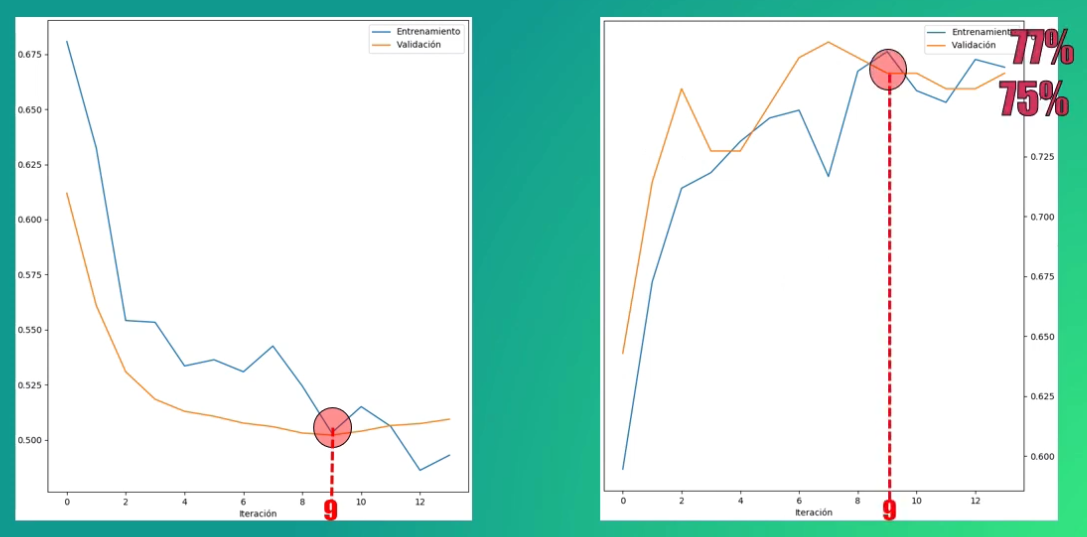
Comportamiento del error (izquierda) y la precisión (derecha) para los sets de entrenamiento y validación del modelo con early stopping

En este caso los valores obtenidos para la precisión con los sets de entrenamiento y validación son de aproximadamente 75 y 77%. Es decir, que con este cuarto modelo entrenado ¡prácticamente no existe overfitting!

Conclusión

Bien, en este video vimos un ejemplo práctico de un modelo con overfitting y de cómo atacar este problema usando tres estrategias diferentes.

La primera de ellas consistió en simplificar el modelo, usando menos capas y menos neuronas por capa. La segunda técnica, que es tal vez la más usada y efectiva, es el Dropout, que consiste en desactivar en cada iteración del entrenamiento, y de forma aleatoria, un cierto porcentaje de las neuronas de cada capa. Y la tercera es el early stopping, que consiste en detener el entrenamiento en el momento en que el error del set de validación se comienza a incrementar.

En estos tres casos vimos que se lograba mejorar la precisión con el set de validación, pasando de 60% a aproximadamente un 70%.

En todo caso vemos que esta precisión sigue siendo relativamente baja para lo que se espera de un clasificador, y esto nos indica que de todos modos el modelo presenta algo de underfitting. En el siguiente post veremos, también con un ejemplo práctico, cómo resolver este problema y mejorar así la precisión con el set de validación.

Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:

Datos y código fuente

En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.