Tutorial Python: ¿Cómo reducir el Underfitting?

Diciembre 16, 2019 por Miguel Sotaquirá

En este artículo veremos en detalle cómo resolver el problema del underfitting en un modelo de Deep Learning. Para ello clasificaremos un set de imágenes usando dos modelos diferentes: Redes Neuronales y Redes Convolucionales.

Veremos que en el primer caso habrá underfitting, mientras que el uso de la Red Convolucional eliminará casi por completo este problema. Con esto verificaremos que muchas veces la estrategia para reducir o eliminar por completo el underfitting es utilizar una arquitectura adecuada para el tipo de dato que queremos procesar.

Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.

Así que, ¡listo, comencemos!

Tabla de contenido

Video

Como siempre, en el canal de YouTube se encuentra el video de este post:

Introducción

En el primer post de esta serie vimos una explicación detallada del underfitting, que se da cuando el modelo (bien sea una red neuronal o una convolucional) no tiene un desempeño adecuado con el set de entrenamiento ni tampoco con el de validación.

Lectura y pre-procesamiento del set de datos

El set de datos que vamos a usar en este tutorial se conoce como CIFAR. El set contiene imágenes a color, cada una de 32x32 pixeles y pertenecientes a 10 posibles categorías. En total 60.000 imágenes: 50.000 de entrenamiento y 10.000 para validación:

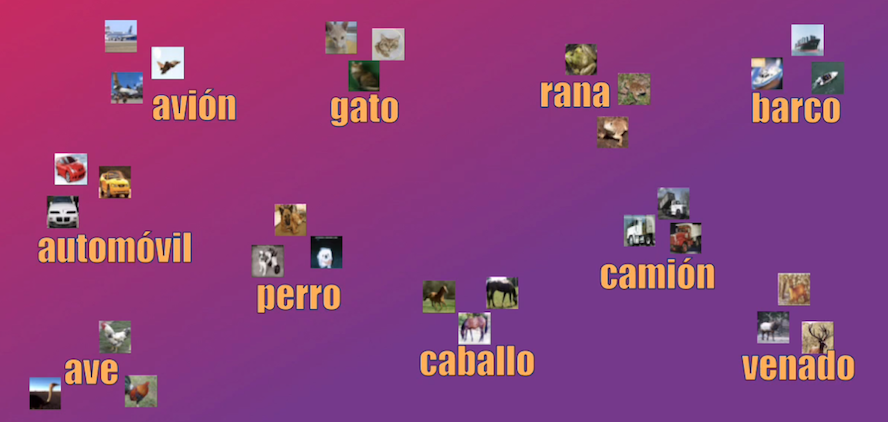
La idea es desarrollar un modelo que sea capaz de clasificar con una alta precisión estas imágenes.

Primero hagamos la lectura y el pre-procesamiento. La lectura es sencilla, y podemos usar el módulo cifar10 de Keras para descargar y leer automáticamente los datos:

from keras.datasets import cifar10

(X_train, y_train), (X_test, y_test)= cifar10.load_data()

Como se trata de imágenes a color, cada una de ellas será una matriz de 32 filas x 32 columnas con 3 planos de color: Rojo, verde y azul. Cada pixel, en cada uno de esos planos de color, está representado con un valor de 0 a 255:

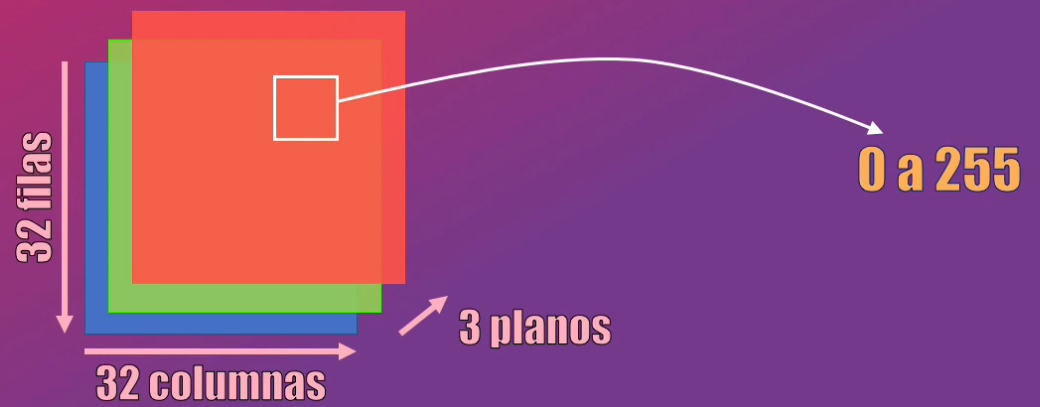
Características de cada imagen perteneciente al set de datos

Como parte del pre-procesamiento debemos normalizar el valor de cada pixel de la imagen, para que en lugar de 0 a 255 esté en el rango de 0 a 1, lo que facilitará la convergencia del entrenamiento de los modelos a implementar. Esto se logra fácilmente dividiendo cada pixel precisamente entre 255:

X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train = X_train / 255.0
X_test = X_test / 255.0

Finalmente, debemos convertir las variables y_train y y_test (que contienen la categoría a la que corresponde cada imagen) al formato one-hot. Esto quiere decir que para cada una de las diez posibles categorías, la etiqueta será representada como un número binario con 10 elementos en donde sólo uno de ellos será 1 y todos los demás serán 0:

$$0 \rightarrow [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]$$ $$1 \rightarrow [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]$$ $$…$$ $$9 \rightarrow [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]$$

Esta representación es requerida por Keras al momento de entrenar los modelos.

Esta conversión al formato one-hot se logra fácilmente usando la función to_categorical de Keras:

from keras.utils import to_categorical

Y_train = to_categorical(y_train)
Y_test = to_categorical(y_test)

Con este pre-procesamiento ya estamos listos para crear nuestro primer modelo y analizar su desempeño.

Modelo 1: Red Neuronal con Underfitting

Creemos un primer modelo correspondiente a una Red Neuronal. En realidad una Red Neuronal no es la más adecuada para clasificar una imagen (para esto están las redes convolucionales) pero esto lo hacemos intencionalmente para evidenciar el problema de underfitting.

Como la Red Neuronal acepta vectores (no matrices) a la entrada, debemos “aplanar” cada imagen en el set de entrenamiento y de validación:

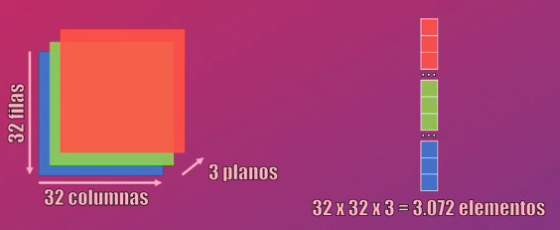
Cada imagen (matriz de tres dimensiones) debe ser convertida a un vector antes de introducirla al modelo

Esto se logra usando la función reshape de Numpy:

import numpy as np

m = X_train.shape[0]			# Número de datos de entrenamiento
n = X_test.shape[0]				# Número de datos de validación
nrows, ncols, nplanos = X_train.shape[1], X_train.shape[2], X_train.shape[3]

X_train = np.reshape(X_train, (m, nrows*ncols*nplanos))
X_test = np.reshape(X_test, (n, nrows*ncols*nplanos))

Con esto cada ejemplo de entrenamiento y validación será un vector de $32 \cdot 32 \cdot 3 = 3.072$ elementos.

Creacion del modelo en Keras

La Red Neuronal tendrá una capa de entrada que aceptara vectores de 3.072 (es decir del tamaño de cada ejemplo de entrenamiento y validación). Contendrá una sola capa oculta con 15 neuronas y función de activación ReLU. Y la salida tendrá una función de activación softmax que nos permitirá clasificar cada dato de entrada en una de 10 posibles categorías.

Esta arquitectura se puede implementar fácilmente usando los módulos Sequential y Dense de Keras:

np.random.seed(1)
from keras.models import Sequential
from keras.layers import Dense

input_dim = X_train.shape[1]
output_dim = Y_train.shape[1]

modelo = Sequential()
modelo.add( Dense(15, input_dim=input_dim, activation='relu'))
modelo.add( Dense(output_dim, activation='softmax'))

En donde hemos usado np.random.seed(1) para fijar la semilla del generador aleatorio y garantizar así la reproducibilidad del entrenamiento (es decir que lleguemos a los mismos resultados cada vez que ejecutemos el código).

Entrenamiento del modelo

Para el entrenamiento usaremos el algoritmo del Gradiente Descendente con una tasa de aprendizaje de 0.05:

from keras.optimizers import SGD

sgd = SGD(lr=0.05)

La función de error a minimizar será la entropía cruzada (categorical_crossentropy), que es la misma usada en la Regresión Multiclase, y nuestra métrica de desempeño será la precisión (accuracy):

modelo.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])

Para el entrenamiento usaremos la función fit de Keras. Tendremos en total 2000 iteraciones (epochs) de entrenamiento, y presentaremos los datos al modelo en bloques de 1024 datos (batch_size):

num_epochs = 2000
batch_size = 1024
historia = modelo.fit(X_train, Y_train, validation_data = (X_test,Y_test),epochs=num_epochs, batch_size=batch_size, verbose=2)

En la última línea de código anterior hemos usado validation_data = (X_test,Y_test) para validar el modelo de forma simultánea con el entrenamiento.

Resultado del entrenamiento: underfitting

Una vez realizado este entrenamiento observamos que la precisión del modelo con los datos de entrenamiento es cercana a tan solo el 50%, mientras que para los datos de validación es de tan sólo el 45%. Aunque se observa que la precisión para el set de entrenamiento podría mejorar con más iteraciones, se observa que no ocurrirá lo mismo con el set de validación:

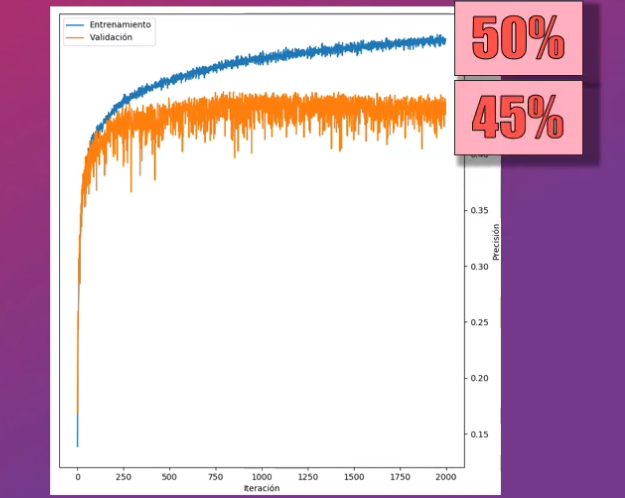
Resultado del entrenamiento del primer modelo, en donde se observa la presencia de underfitting

Con este modelo tenemos un claro ejemplo de underfitting: la Red Neuronal no es capaz de clasificar correctamente ninguno de los dos sets, y la precisión es inferior al 50%.

Como lo mencionabamos en un post anterior, una de las causas del underfitting es que el modelo es demasiado simple para la complejidad de los datos. En este caso tenemos una Red Neuronal con tan sólo una capa oculta.

Modelo 2: Red Neuronal con dos capas ocultas

Veamos qué ocurre si hacemos el modelo más complejo, agregando otra capa oculta. Creemos entonces una segunda Red Neuronal, con una primera capa oculta con 30 neuronas y una segunda capa con 15 neuronas, adicionales a las capas de entrada y de salida originales:

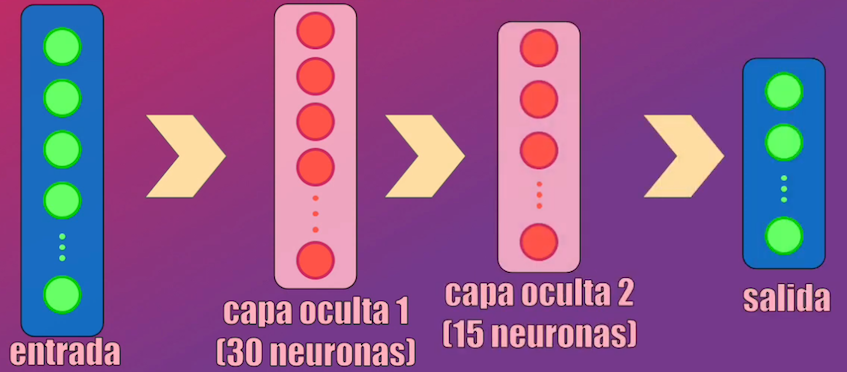
Estructura del modelo 2 para la clasificación del set de datos

La creación del modelo y su entrenamiento en Keras es prácticamente idéntica a la usada en el modelo anterior, con la excepción de que al inicio se deben crear las dos capas ocultas mencionadas anteriormente:

input_dim = X_train.shape[1]
output_dim = Y_train.shape[1]

modelo = Sequential()
modelo.add( Dense(30, input_dim=input_dim, activation='relu'))
modelo.add( Dense(15, activation='relu'))
modelo.add( Dense(output_dim, activation='softmax'))

# Compilación y entrenamiento: gradiente descendente, learning rate = 0.05, función
# de error: entropía cruzada, métrica de desempeño: precisión

sgd = SGD(lr=0.05)
modelo.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])

# Para el entrenamiento se usarán 2000 iteraciones y un batch_size de 1024
num_epochs = 2000
batch_size = 1024
historia = modelo.fit(X_train, Y_train, validation_data = (X_test,Y_test),epochs=num_epochs, batch_size=batch_size, verbose=2)

Al validar este nuevo modelo vemos que efectivamente la precisión del set de entrenamiento se incrementa (pasó del 50 al 65%) pero la precisión del set de validación se mantiene prácticamente igual, en el 45%:

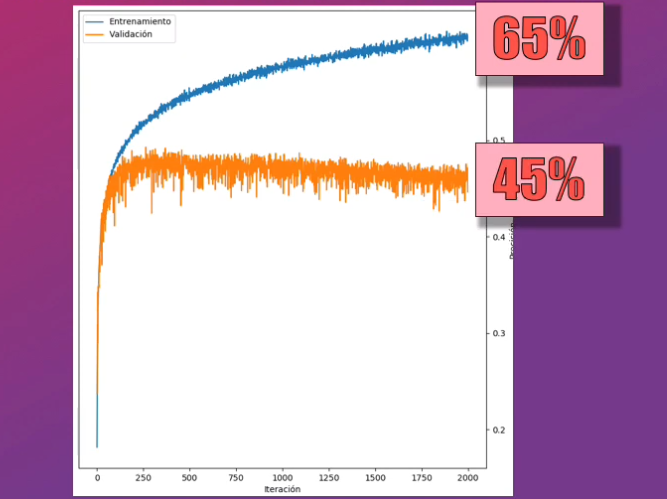
Resultado del entrenamiento del segundo modelo, en donde se observa que aún hay presencia de underfitting

Lo anterior quiere decir que a pesar de contar un modelo más complejo sigue existiendo underfitting. Este resultado nos indica que probablemente una Red Neuronal no es la arquitectura más adecuada para clasificar las imágenes.

Modelo 3: Red Convolucional

¿Y qué pasa si usamos una Red Convolucional, que es una arquitectura diseñada específicamente para procesar imágenes?

Creación de la Red Convolucional en Keras

Creemos una Red Convolucional con tres capas, todas ellas con filtros convolucionales de 3x3. La primera capa tendrá dos bloques de 32 filtros, la segunda de 64 y la tercera de 128, todas ellas seguidas por bloques maxpooling.

Esta estructura la podemos crear fácilmente en Keras usando, de nuevo, el módulo Sequential así como los módulos Conv2D y MaxPooling2D:

from keras.layers import Conv2D
from keras.layers import MaxPooling2D

X_train = np.reshape(X_train,(m,nrows,ncols,nplanos))
X_test = np.reshape(X_test,(n,nrows,ncols,nplanos))

# Creacion de la red convolucional

modelo = Sequential()
modelo.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(32, 32, 3)))
modelo.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
modelo.add(MaxPooling2D((2, 2)))

modelo.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
modelo.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
modelo.add(MaxPooling2D((2, 2)))

modelo.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
modelo.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
modelo.add(MaxPooling2D((2, 2)))

En donde en las líneas 3 y 4 hemos modificado X_train y X_test para que en lugar de ser vectores sean matrices (cada una de 32x32x3) como lo requiere la Red Convolucional.

A la salida de estas capas aplanaremos el dato (usando Flatten) y lo conectaremos a una Red Neuronal (usando Dense) con 128 neuronas y posteriormente a la salida, correspondiente a la activación softmax:

modelo.add(Flatten())
modelo.add(Dense(128, activation='relu', kernel_initializer='he_uniform'))
modelo.add(Dense(10, activation='softmax'))

Entrenamiento de la Red Convolucional

El entrenamiento será muy similar al realizado en los dos modelos anteriores, con la única diferencia de que se usará una tasa de aprendizaje diferente, y tan sólo 100 iteraciones con un tamaño de lote de 64:

opt = SGD(lr=0.001, momentum=0.9)
modelo.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])

historia = modelo.fit(X_train, Y_train, epochs=100, batch_size=64, validation_data=(X_test, Y_test), verbose=2)

Resultado del entrenamiento

Al realizar el entrenamiento de esta Red Convolucional vemos un incremento significativo en la precisión, que es ahora de casi el 90% para el set de entrenamiento y de casi el 85% para el set de validación:

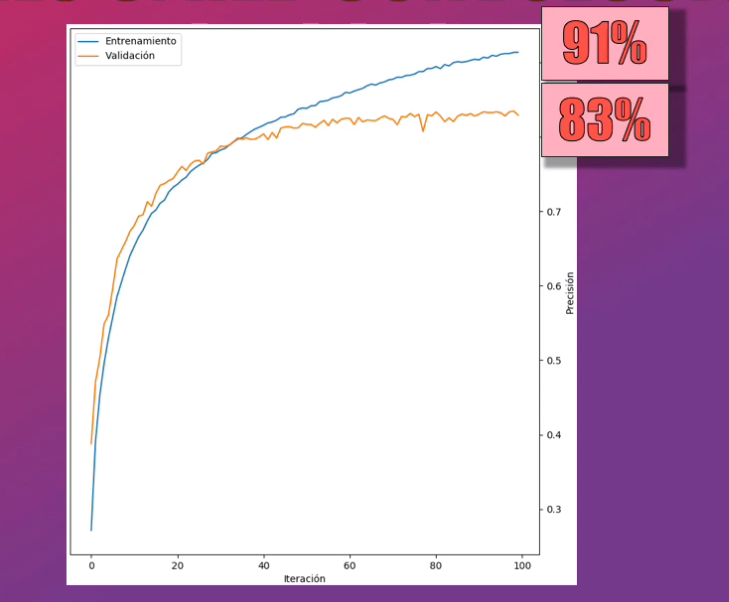
Es evidente que ya el modelo no presenta underfitting, y esto obedece precisamente a que estamos usando una arquitectura adecuada para procesar estas imágenes.

Conclusión

Bien, en este post vimos un ejemplo práctico de cómo reducir el problema de underfitting al desarrollar un modelo de Deep Learning.

En particular vimos que una Red Neuronal presenta underfitting en este caso particular, dada la complejidad de las imágenes utilizadas. Esto era prácticamente independiente de la complejidad de la red, pues con más o menos capas ocultas la precisión con el set de validación era prácticamente la misma (un 45%).

Sin embargo, este resultado nos dio una indicación importante: probablemente la Red Neuronal no era la arquitectura más adecuada para este tipo de datos. Al modificarla por una Red Convolucional vimos que la precisión alcanzada en ambos sets superó el 85%.

Así, muchas veces una estrategia para reducir o eliminar por completo el underfitting es utilizar una arquitectura adecuada para el tipo de dato que queremos procesar.

Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:

Datos y código fuente

En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.