Tutorial: el Gradiente Descendente en Python
En este tutorial veremos como programar paso a paso el algoritmo del Gradiente Descendente en Python, sin usar ninguna librería de Machine Learning.
Usando una sencilla función matemática, veremos cómo inicializar las variables del algoritmo, cómo definir el número de iteraciones y la tasa de aprendizaje y, finalmente, cómo encontrar el mínimo de esta función usando el algoritmo del Gradiente Descendente. Veremos además el efecto que el número de iteraciones y la tasa de aprendizaje tienen en la convergencia del algoritmo.
Al final del artículo se encuentra el enlace para descargar el código fuente de este tutorial.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Implementación del Gradiente Descendente en Python
Para entender este tutorial te recomiendo leer el artículo en donde explico en detalle el algoritmo del Gradiente Descendente. En este tutorial veremos cómo programar este algoritmo en Python para minimizar una función.
En particular, obtendremos de forma automática el mínimo de la función $y = x^2 + 1$, y analizaremos el efecto que la tasa de aprendizaje tiene en el comportamiento del algoritmo.
En la figura de abajo se observa la función y, donde podemos verificar que el valor mínimo se obtiene cuando x = 0:
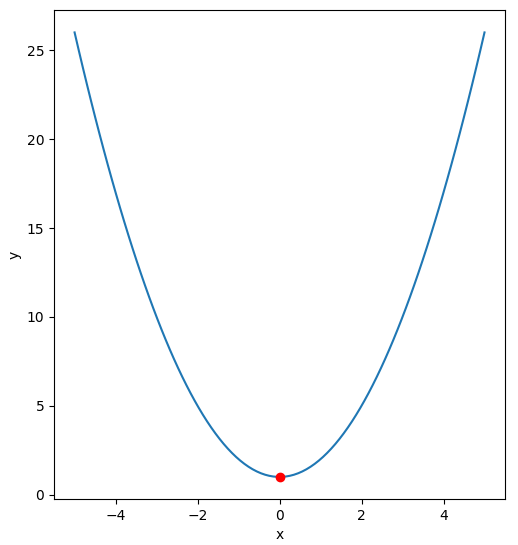
Veamos entonces cómo implementar el algoritmo paso a paso.
Librerías requeridas
En este caso necesitamos las librerías Numpy(para la generación de números aleatorios y para almacenar las variables en memoria) y Matplotlib para graficar los resultados del algoritmo.
Inicialización de variables
Para implementar el algoritmo del Gradiente Descendente en Python, primero debemos inicializarlo con un valor x escogido aleatoriamente, y además debemos especificar el número de iteraciones y la tasa de aprendizaje (α). Usaremos una tasa de aprendizaje de 0.3 y un total de 15 iteraciones.
Estas variables se pueden definir con las siguientes líneas de código:
x_inicial = randint(10)
alpha = 0.3
n_iteraciones = 15
en donde en la primera línea hemos hecho uso de la función `randint de numpy para generar un número entero aleatorio en el rango de 0 a 10.
Cálculo del mínimo a partir del método del gradiente descendente
Primero crearemos dos listas, iteraciones y `y, que permitirán almacenar el número de la iteración así como el valor de la función durante la ejecución del código:
iteraciones = []
y = []
Teniendo en cuenta que $y = x^2 + 1$, podemos obtener entonces el gradiente de esta función, necesario para la implementación del gradiente descendiente en Python:
gradiente = 2x
Con esta información podemos implementar el algoritmo en Python. En primer lugar asignamos el valor inicial de la variable x (`x = x_inicial) y posteriormente realizamos las iteraciones, actualizando el valor de x en cada iteración según la fórmula del gradiente descendente:
x ← x -α.gradiente
De igual forma, almacenamos el número de la iteración y el valor resultante de la función en las variables iteraciones y y respectivamente, e imprimimos los resultados de cada iteración en la pantalla.
El código completo es el siguiente:
x = x_inicial
for i in range(n_iteraciones):
print('------------------------')
print('iteración ', str(i+1))
# Calcular gradiente
gradiente = 2*x
# Actualizar "x" usando gradiente descendente
x = x - alpha*gradiente
# Almacenar iteración y valor correspondiente
y.append(x**2 + 1)
iteraciones.append(i+1)
# Imprimir resultados
print('x = ', str(x), ', y = ', str(x**2+1))
Resultados
Veamos qué ocurre al ejecutar el codigo para el algoritmo del Gradiente Descendente en Python. Con una tasa de aprendizaje de 0.3, se requieren aproximadamente cuatro iteraciones para lograr la convergencia del algoritmo:
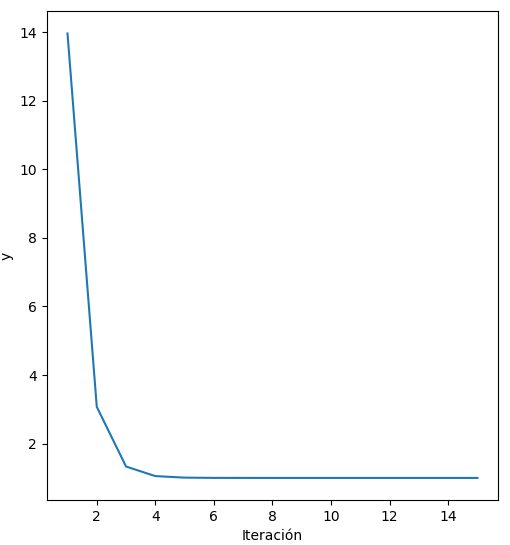
Al incrementar la tasa de aprendizaje a 0.6 el número de iteraciones requerido disminuye, siendo necesarias aproximadamente tres:
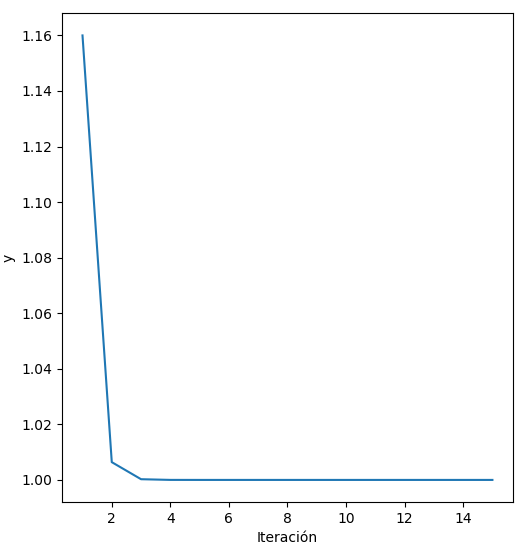
Si reducimos el valor de la tasa de aprendizaje a 0.1, se requerirán casi catorce iteraciones para la convergencia:
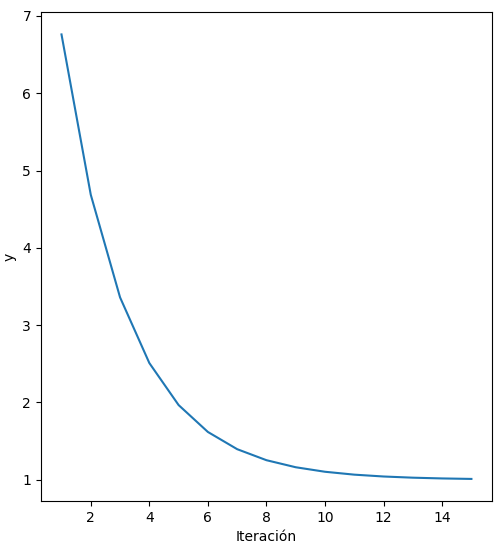
Los ejemplos anteriores permiten verificar lo discutido en la explicación del método del gradiente descendente, pues un incremento en el valor de alpha reduce el número de iteraciones requeridas para hacer que el algoritmo converja.
Código fuente
En este enlace de Github podrás descargar el código fuente de este tutorial.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: