¿Qué es el Gradiente Descendente?
En este post veremos qué es y cómo funciona el Gradiente Descendente, un algoritmo esencial pues es la base de todos los algoritmos de entrenamiento de modelos Machine Learning (como las Redes Neuronales, Convolucionales, Recurrentes y Transformer).
Este algoritmo de optimización permite encontrar de forma automática el mínimo de una función. Para ello hace uso de el gradiente (o derivada) de dicha función, que permite “guiar” al algoritmo para de manera progresiva acercarse al mínimo ideal de dicha función.
Además de comprender cómo funciona el algoritmo, en este video analizaremos el efecto que tiene la tasa de aprendizaje y el número de iteraciones, parámetros que son definidos por el usuario y que determinarán la convergencia adecuada del algoritmo, y que además son dos de los parámetros de mayor importancia durante el entrenamiento de un modelo de Machine Learning.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Además, en el siguiente enlace podrás encontrar un tutorial con la implementación del Gradiente Descendente en Python.
¿Qué es el mínimo de una función?
El Gradiente Descendente es un algoritmo computacional que permite determinar de forma automática el mínimo de una función matemática.
Para entender esta idea observemos la figura de abajo, correspondiente a la función $e = w^2 + 1$. El mínimo de la función corresponde al punto de color rojo, y se obtiene cuando w alcanza un valor igual a 0. Así, la ubicación del mínimo es el punto w=0, e=1:
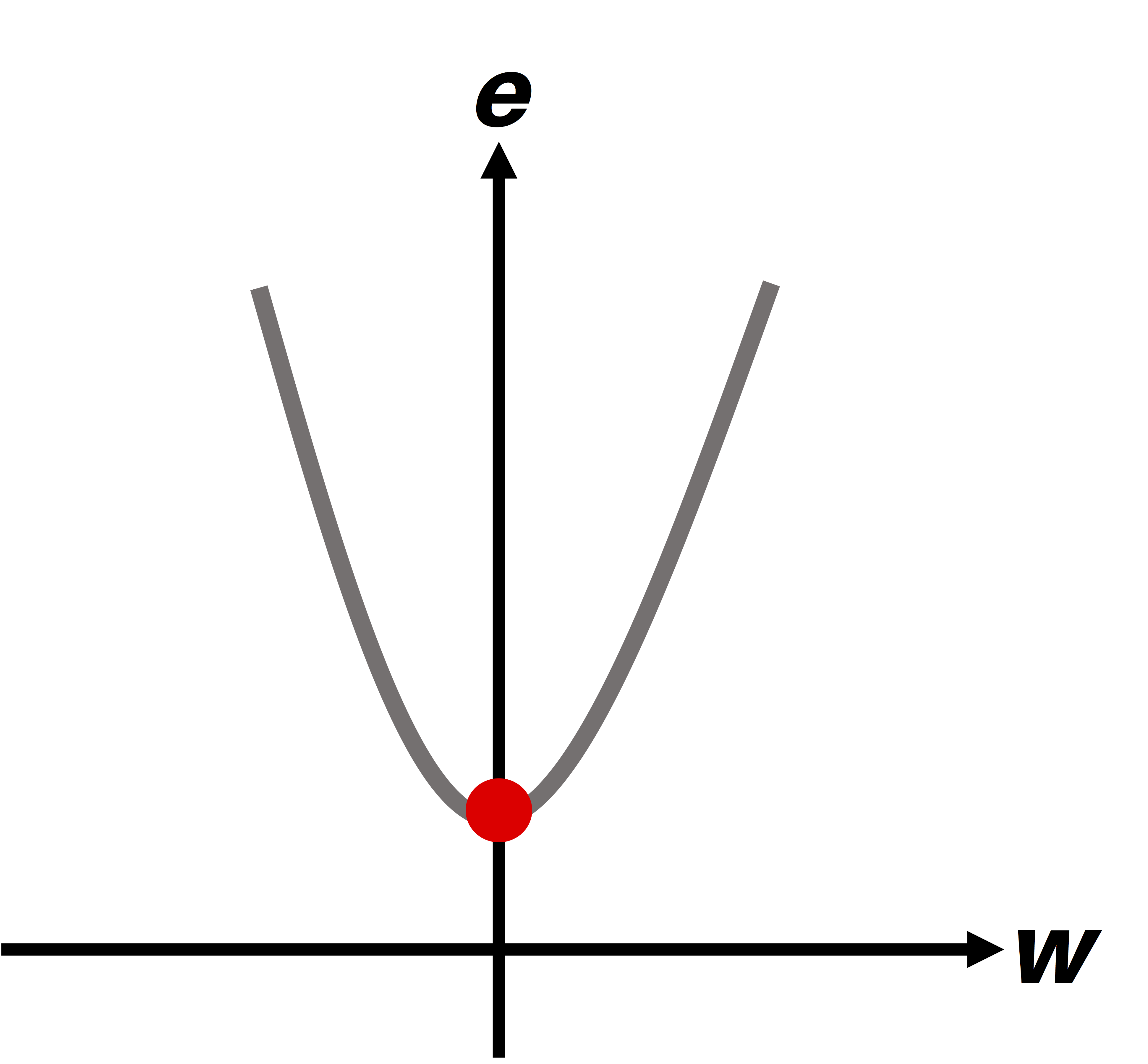
El algoritmo del gradiente descendente permite entonces encontrar de forma automática el punto w=0. Para entender cómo funciona es necesario entender el concepto de gradiente, discutido a continuación.
¿Qué es el Gradiente?
El Gradiente es sinónimo de pendiente o inclinación, y matemáticamente recibe el nombre de derivada.
Entendamos esto a través de un ejemplo. En la figura de abajo se ilustra la misma función e mencionada anteriormente, junto con la representación gráfica del gradiente en tres puntos diferentes:
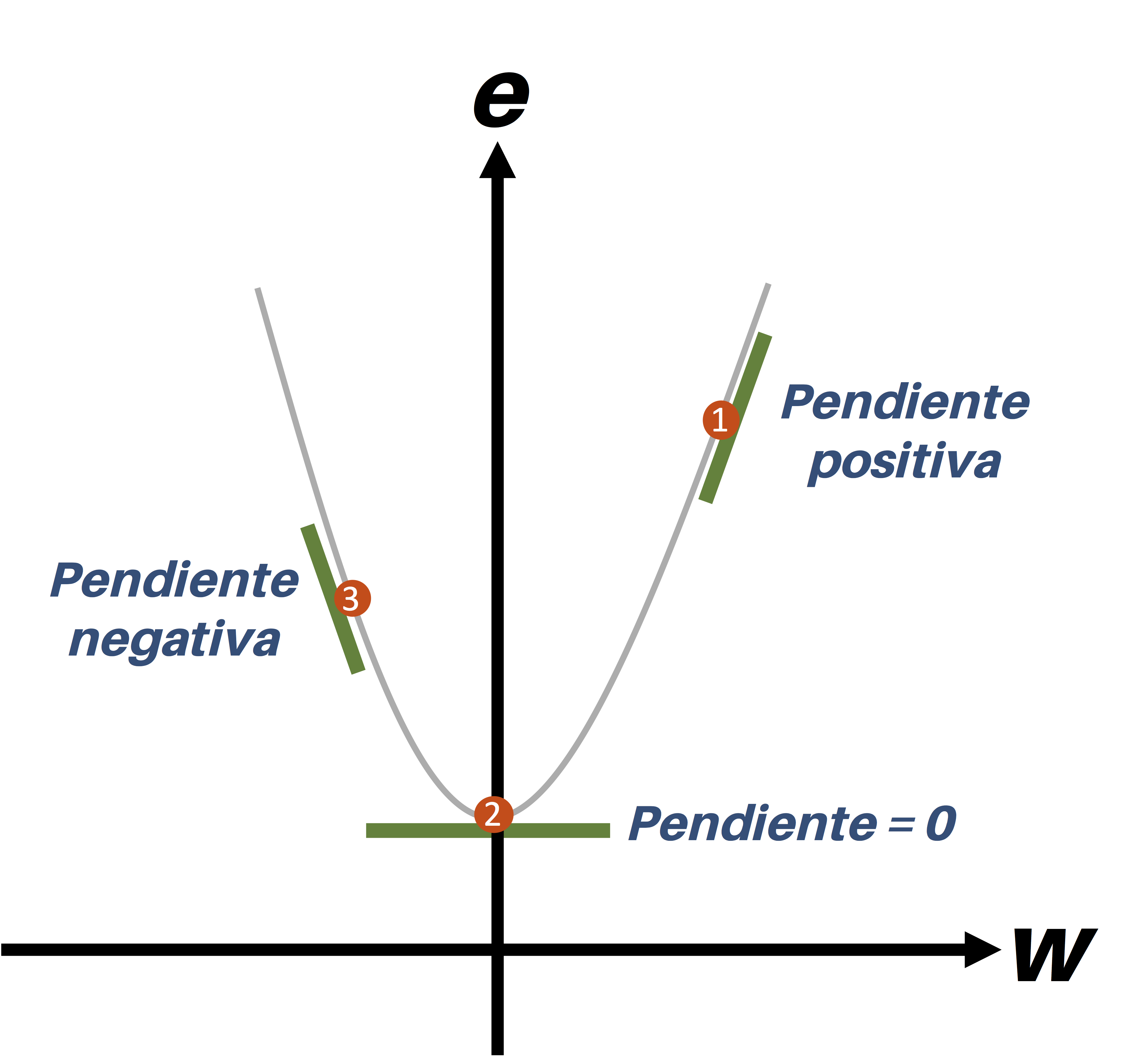
En el punto 1 se observa una línea con una inclinación correspondiente a un gradiente positivo, mientras que en el punto 3 la línea tiene una orientación opuesta y por tanto se dice que tiene una pendiente negativa. Por su parte, en el punto 2 la línea es totalmente horizontal y carece de inclinación, por lo que se dice que su pendiente es igual a cero.
Teniendo este concepto claro, veamos ahora en qué consiste el algoritmo del Gradiente Descendente.
¿Cómo funciona el algoritmo del Gradiente Descendente?
El algoritmo es iterativo (es decir que se repite el mismo procedimiento varias veces) y requiere que el usuario introduzca dos parámetros:
- El número de iteraciones, es decir cuántas veces se repetirá el procedimiento
- La tasa de aprendizaje (o learning rate), conocido como el parámetro α. Este definirá la cantidad de iteraciones requerida para que el algoritmo encuentre el mínimo de la función.
Una vez definidos estos dos parámetros, el algoritmo procede de la siguiente manera:
- Escoge de forma aleatoria el valor inicial de la variable $w$
- En cada iteración actualiza el valor de w usando la siguiente ecuación: w ← w - α . gradiente
Se repite el paso (2) hasta completar el número de iteraciones definido por el usuario.
Entendamos el algoritmo a través de un ejemplo gráfico.
Ejemplo de funcionamiento del algoritmo
En la figura de abajo vemos una ilustración del funcionamiento del algoritmo. En primer lugar, el punto inicial “0” es seleccionado aleatoriamente:
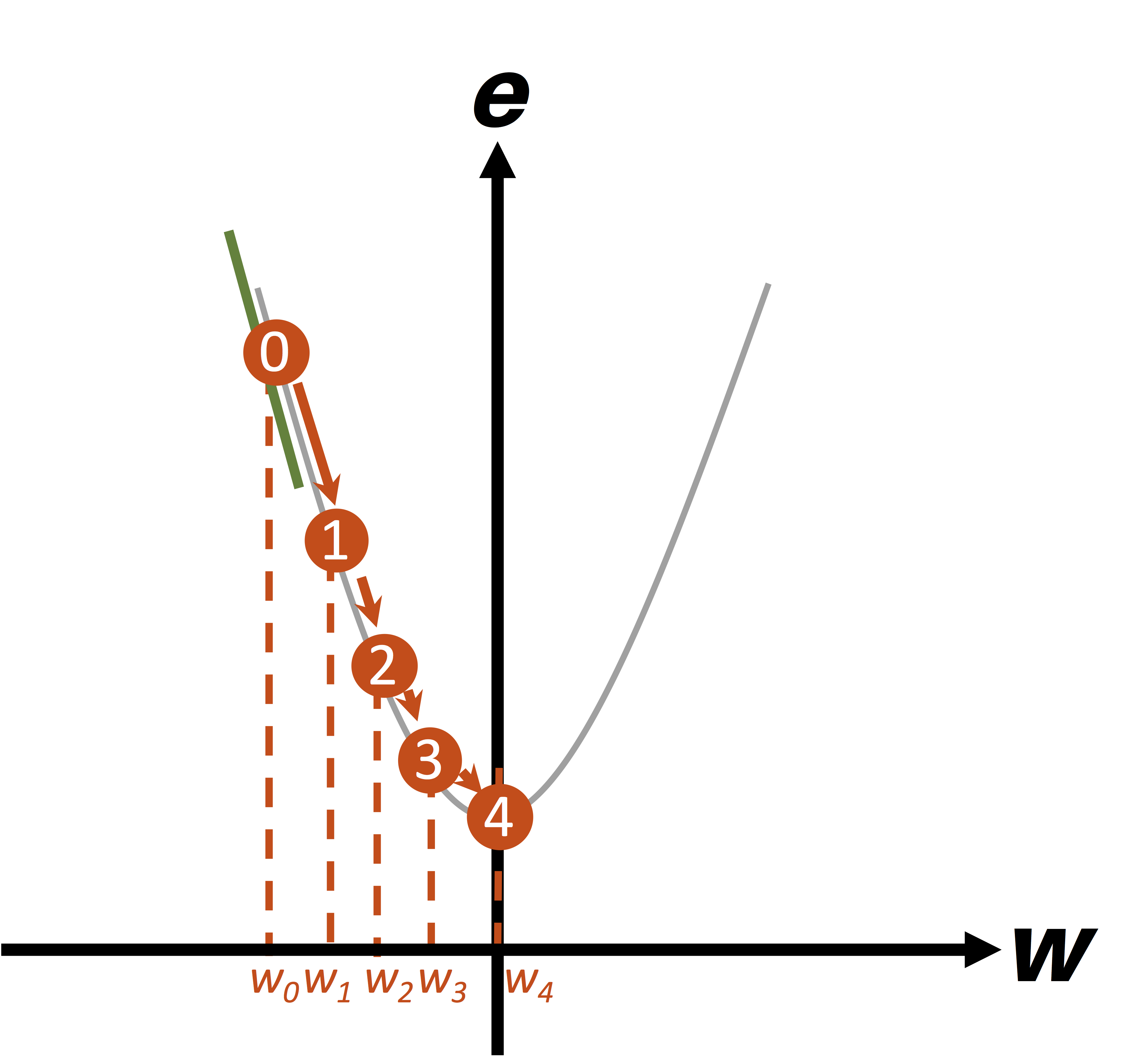
En la primera iteración se calcula el gradiente en el punto 0, que corresponde a la línea recta de color verde en la gráfica. Se observa que este gradiente es negativo, y por tanto la cantidad -α . gradiente es un número positivo, lo cual quiere decir que al valor inicial de $w_0$ se sumará el término positivo -α . gradiente, y por tanto $w_1$ estará ubicado a la derecha del punto inicial.
En la segunda iteración el gradiente seguirá siendo negativo, y por tanto el término -α . gradiente será nuevamente positivo, lo cual quiere decir que el nuevo valor $w_2$ estará ubicado a la derecha de $w_1$.
Si se repite el procedimiento podemos observar que en cada iteración el nuevo valor de w calculado está cada vez más cerca del valor mínimo buscado (w=0).
Algo similar ocurre cuando el punto inicial (w) es positivo, como se muestra en la figura de abajo:
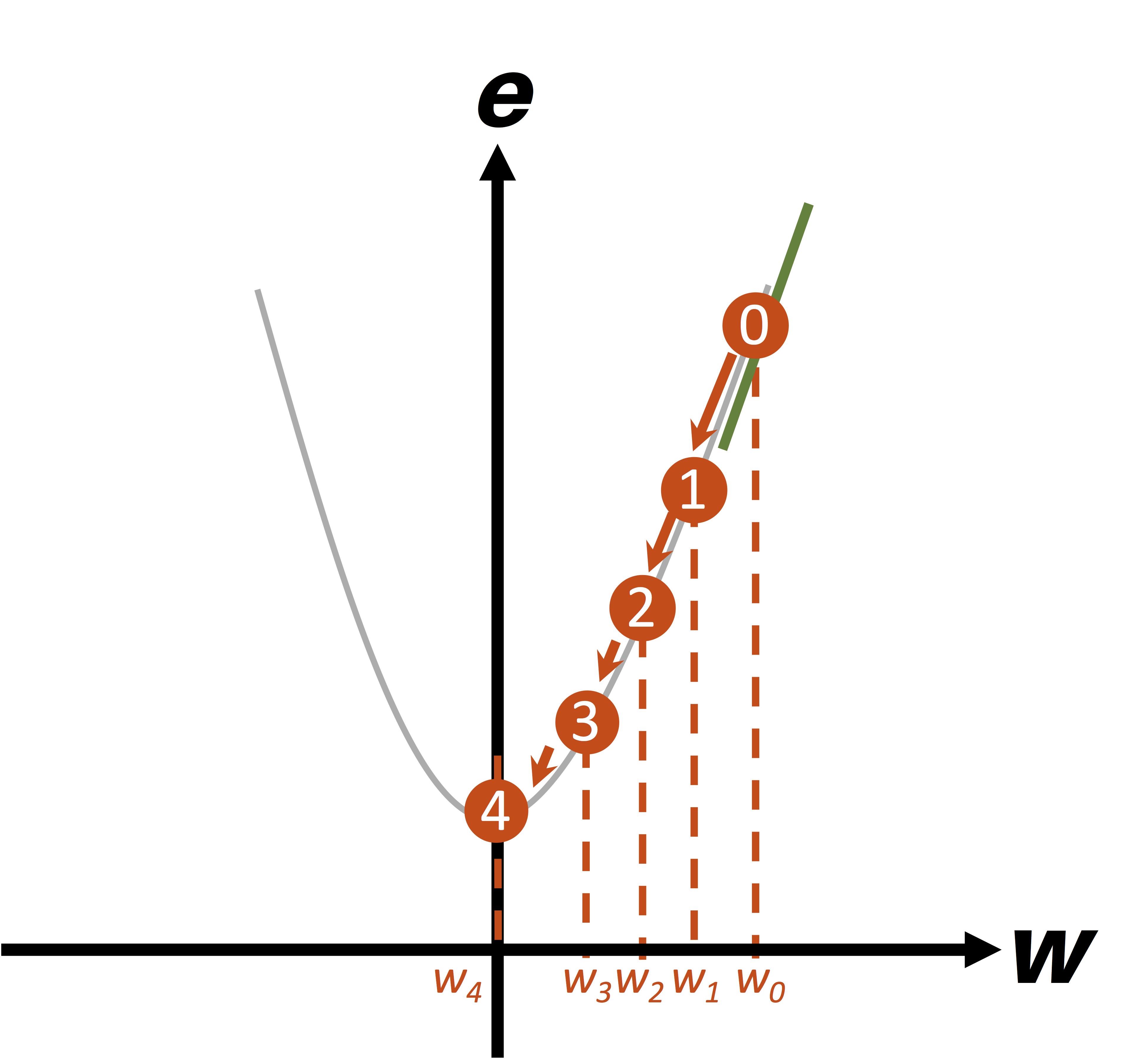
Veamos ahora el efecto que tiene el parámetro α (o learning rate) en el funcionamiento del algoritmo.
Efecto de la tasa de aprendizaje (α)
El gradiente o derivada de la función $e = w^2 + 1$ es igual a 2w. Para simular el comportamiento del algoritmo, supongamos inicialmente un valor $w_0 = 5$ y una tasa de aprendizaje α = 0.25.
Así, en la primera iteración del algoritmo tendremos:
- $w_0= 5$
- Gradiente (=2w) = 2x5 = 10
- $w_1 = w_0 - α.gradiente$ = 5 - 0.25x10 = 5-2.5 = 2.5
Al repetir el procedimiento obtenemos los siguientes resultados en las iteraciones 2 a 6:
- $w_2 = 1.25$
- $w_3 = 0.625$
- $w_4 = 0.3125$
- $w_5 = 0.156$
- $w_6 = 0.078$
Y podemos observar que en este caso se requieren aproximadamente 6 iteraciones para que el valor de w sea casi cero.
Si ahora se usa una tasa de aprendizaje α = 0.4, y repetimos el mismo procedimiento anterior, veremos que en lugar de 5 se requieren tan solo 3 iteraciones para que w alcance el valor de 0.04:
- $w_1 = 1.0$
- $w_2 = 0.2$
- $w_3 = 0.04$
Si consideramos la situación extrema α = 1.0, observamos el siguiente comportamiento:
- $w_1 = -5$
- $w_2 = 5$
- $w_3 = -5$
- $w_4 = 5$
- $w_5 = -5$
- $w_6 = $
Así, el valor de w alterna entre 5.0 y -5.0 y nunca disminuye. En este caso decimos que el algoritmo no converge y por tanto nunca encontrará un valor mínimo.
Los anteriores ejemplos nos permiten concluir que la tasa de aprendizaje α determina la cantidad de iteraciones requeridas para que el algoritmo del gradiente descendente alcance el valor mínimo, y el valor seleccionado dependerá de la función a minimizar (sin embargo siempre debe ser menor a 1).
Conclusión
El algoritmo del gradiente descendente es uno de los métodos más usados durante el proceso de entrenamiento de un Modelo de Machine Learning, y es usado prácticamente para implementar cualquier arquitectura, desde las Redes Neuronales, pasando por las Convolucionales, Recurrentes y LSTM, hasta las Redes Transformer.
Con este método es posible encontrar de forma automática (iterativamente) el valor mínimo de una función matemática. Es importante además tener en cuenta las siguientes consideraciones:
- Como parámetros de entrada el algoritmo requiere el número de iteraciones y la tasa de aprendizaje.
- La tasa de aprendizaje determina la cantidad de iteraciones que serán requeridas para lograr la convergencia del algoritmo.
- Como regla general se debe siempre garantizar que 0 < α < 1 para que el algoritmo converja (es decir para que encuentre el valor mínimo de la función).
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: