La Regresión Lineal en el Machine Learning
En este post veremos en detalle la Regresión Lineal, uno de los algoritmos básicos del Machine Learning. Veremos en detalle los conceptos de error cuadrático medio y como se usa el método del Gradiente Descendente para calcular de forma automática los coeficientes de este modelo lineal.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Además, en el siguiente enlace podrás encontrar un tutorial para la implementación de la Regresión Lineal en Python
Introducción
La Regresión Lineal es un procedimiento que permite encontrar la línea recta que mejor representa la relación entre dos variables.
Supongamos que tenemos una serie de datos como la mostrada en la figura, en donde la variable independiente es x y la variable dependiente es y:
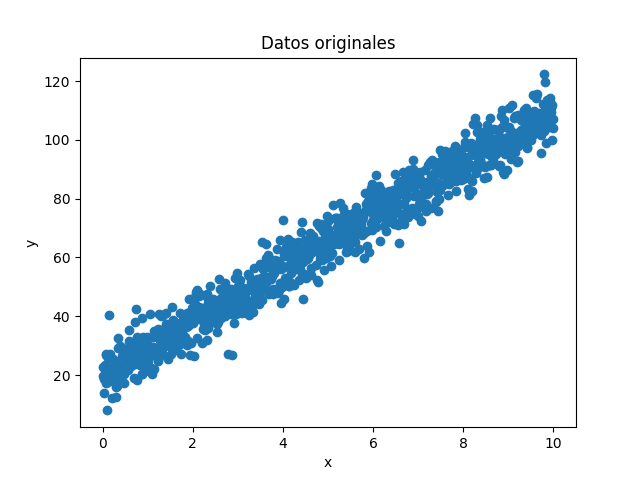
Se observa en esta gráfica que la relación entre las dos variables es lineal, es decir que un incremento en la variable x genera un incremento proporcional en la variable y.
El objetivo de la Regresión Lineal es entonces encontrar la línea recta que mejor se ajusta a los datos.
Para entender la idea anterior veamos la siguiente gráfica, que muestra tres diferentes líneas superpuestas a los datos originales. Es evidente que la recta que mejor describe la relación entre x y y es la línea de color blanco:
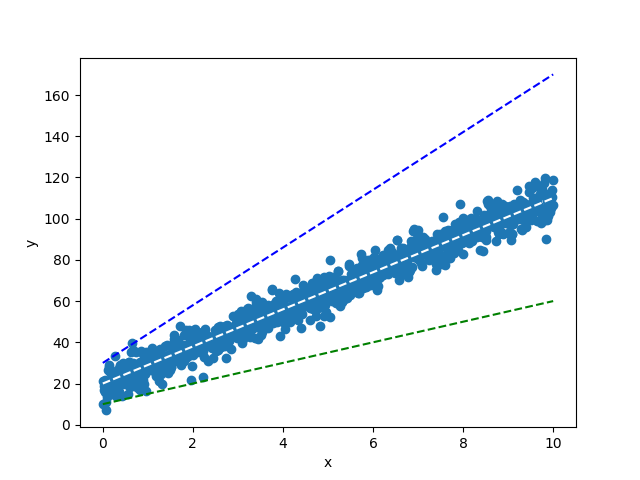
Formulación matemática de la Regresión Lineal
Para resolver el problema de la Regresión Lineal es necesario representar matemáticamente las ideas de “línea recta” y “mejor ajuste”, discutidas a continuación.
Ecuación de una línea recta
La relación lineal entre dos variables x (variable independiente) y y (variable dependiente) se representa matemáticamente a través de la ecuación $y =wx + b$, donde w representa la pendiente (inclinación) de la línea recta y b es la intersección con el eje y.
Así, el objetivo de la Regresión Lineal es encontrar los valores más adecuados de w y b que representen de la mejor forma posible la relación entre las variables x y y.
Para encontrar esta “mejor representación” debemos definir de forma adecuada algún tipo de métrica que nos permita cuantificar qué tan precisa es la Regresión Lineal que estamos realizando. Esta métrica se conoce como función de costo, más comúnmente conocida como pérdida en el ámbito Machine Learning, y discutida a continuación.
Función de costo o pérdida
La pérdida permite medir la diferencia existente entre los datos reales (y) y los datos obtenidos tras realizar la Regresión Lineal (que en adelante llamaremos $\hat{y}$).
Existen diferentes formas de definir matemáticamente esta pérdida, pero la más usada es a través del error cuadrático medio (ECM), definido de la siguiente manera:
$ECM = \displaystyle \frac{1}{N} \sum_{i=1}^{N}\left(y_i-\hat{y}_i\right)^2$
donde N es el número total de datos que se tienen originalmente, $y_i$ y $\hat{y}_i$ son cada uno de los datos originales y los obtenidos a partir de la regresión, y la resta $(y_i-\hat{y}_i)$ se eleva al cuadrado para que todas las diferencias que están en la sumatoria sean positivas y no se cancelen entre sí. Esta resta se ilustra en la siguiente figura:
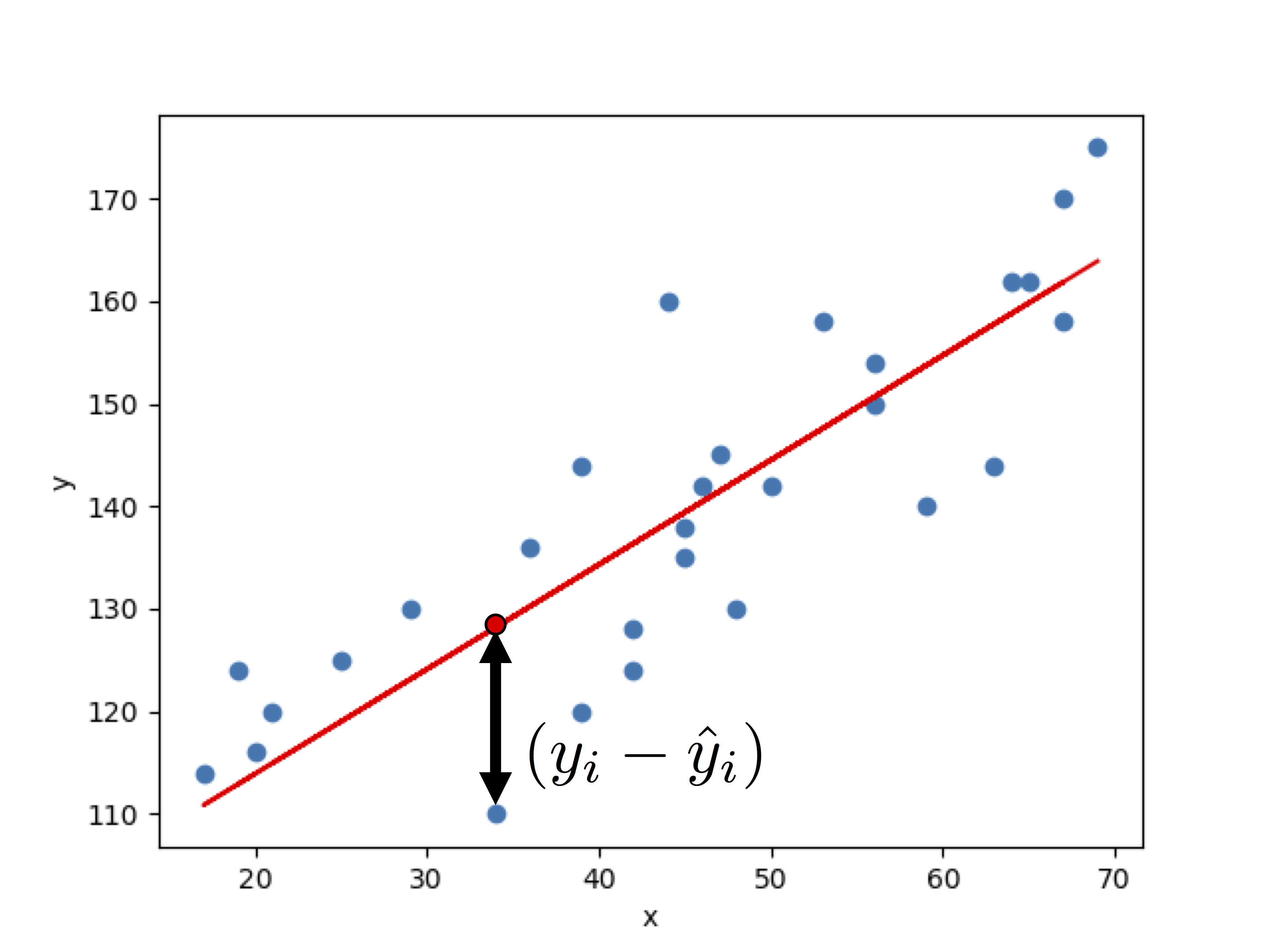
Así, el ECM mide el error promedio existente entre los datos originales y los datos obtenidos a partir de la Regresión Lineal.
Habiendo definido la pérdida, podemos ahora discutir a qué hace referencia el término “mejor ajuste”.
Definición de la línea recta que mejor se ajusta a los datos
Teniendo en cuenta que la pérdida es una medida de la diferencia existente entre los datos originales y la predicción, podemos definir la recta que mejor se ajusta a los datos como aquella que minimiza el error cuadrático medio.
Teniendo en cuenta que cada punto de la regresión se calcula como:
$\hat{y}_i = wx_i + b$
y reemplazando en la ecuación anterior, tenemos que el error cuadrático medio es:
$ECM = \displaystyle \frac{1}{N} \sum_{i=1}^{N}\left(y_i-wx_i-b\right)^2$
Por tanto, la Regresión Lineal es simplemente un problema de optimización, consistente en encontrar los valores w y b óptimos que minimizan la pérdida.
La solución a este problema de optimización se puede encontrar usando el algoritmo del Gradiente Descendente.
Veamos entonces cómo aplicar este método para resolver el problema de la regresión lineal.
La Regresión Lineal y el Gradiente Descendente
Hasta ahora hemos visto que el problema de la Regresión Lineal se reduce a encontrar la línea recta que mejor se ajusta a una serie de datos (x,y), y que esto a su vez equivale a encontrar los parámetros w y b que minimizan la pérdida (ECM).
Pues bien, recordemos que el algoritmo del Gradiente Descendente permite encontrar de forma automática el mínimo de una función, y que únicamente requiere como parámetros de entrada el número de iteraciones y la tasa de aprendizaje.
El Gradiente Descendente
En este caso el Gradiente Descendente se usa para minimizar el ECM, y será una función de dos variables: w y b. Por tanto, al hacer una gráfica de su comportamiento, encontraremos que para el caso de la Regresión Lineal ésta tiene forma de tazón, como se muestra en la figura de abajo. El mínimo que estamos buscando se encuentra al fondo de dicho tazón:
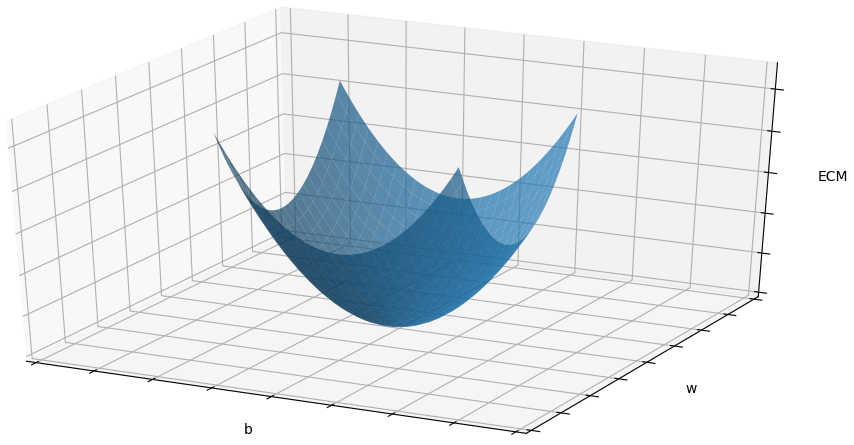
Así, al usar el Gradiente Descendente para minimizar la pérdida, lo que haremos es de forma iterativa calcular los valores de w y b que hacen que el ECM sea cada vez más pequeño (que nos acerquemos progresivamente al fondo del tazón). Para ello usamos la ecuación general del gradiente descendente:
$w \leftarrow w - \alpha dw$
$b \leftarrow b - \alpha db$
donde α es la tasa de aprendizaje y dw y db hacen referencia a la derivada (gradiente) de la pérdida con respecto a los parámetros w y b:
$dw = \displaystyle -\frac{2}{N} \sum_{i=1}^{N}x\left(y_i-wx_i-b\right)$
$db = \displaystyle -\frac{2}{N} \sum_{i=1}^{N}\left(y_i-wx_i-b\right)$
Cálculo de w y b usando el Gradiente Descendente
Al implementar el algoritmo siguiendo las ecuaciones mostradas anteriormente podemos de forma iterativa minimizar la función de error para encontrar la recta que mejor se ajuste a los datos. Esto se observa claramente en la figura de abajo en donde del vemos como de forma iterativa los puntos (w,b) calculados por el algoritmo del Gradiente Descendente se acercan cada vez al valor mínimo del ECM:
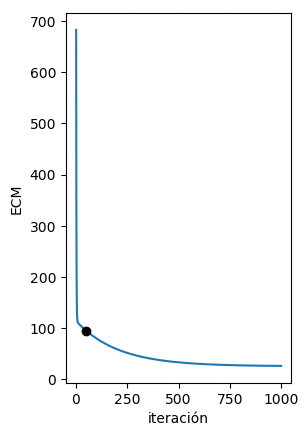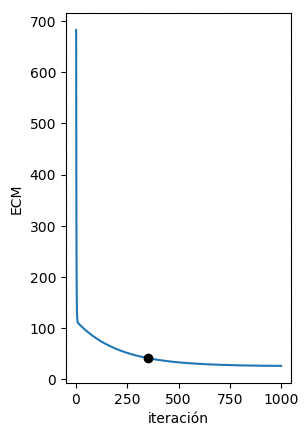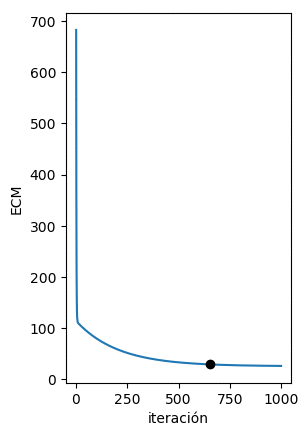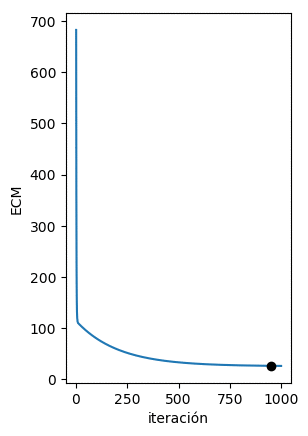
En la siguiente figura podemos ver que en cada iteración la recta obtenida con dichos parámetros se acerca cada vez más a los datos originales:
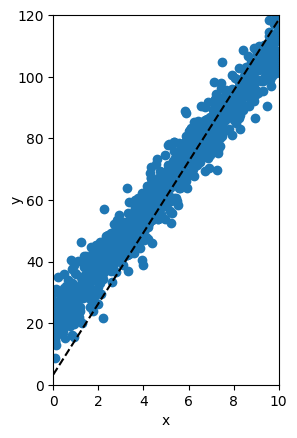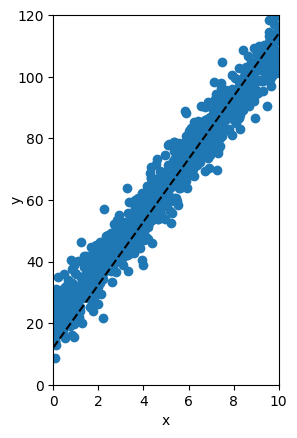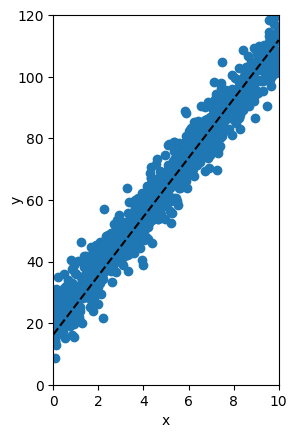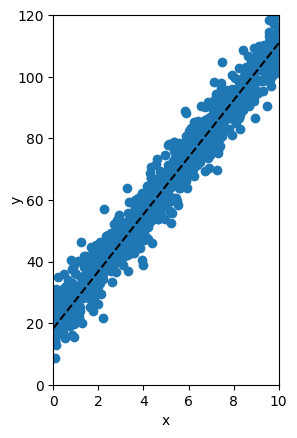
El procedimiento descrito anteriormente, a través del cuál se calculan de forma automática los parámetros w y b usando el método del gradiente descendente, se conoce como proceso de entrenamiento. Esta es una idea fundamental en el desarrollo de modelos de Machine Learning.
Conclusión
En este artículo hemos hablado de la formulación matemática de la Regresión Lineal en el Machine Learning, que es un problema de optimización consistente en encontrar los parámetros w y b de una línea recta para que se ajuste de la mejor manera posible a los datos que conocemos (x,y).
En particular es importante recordar lo siguiente:
- La pérdida es una medida de qué tan bien se ajusta la línea recta a los datos originales.
- En el caso de la Regresión Lineal, esta pérdida usualmente corresponde al error cuadrático medio.
- El mejor ajuste se define matemáticamente como el par de valores w y b que minimizan el error cuadrático medio.
- Este mejor ajuste se puede obtener de forma automática usando el algoritmo del Gradiente Descendente.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: