Tutorial: la Regresión Lineal en Python
En este tutorial veremos paso a paso cómo implementar el algoritmo de Regresión Lineal en Python usando únicamente las librerías Pandas, Numpy y Matplotlib.
Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
El algoritmo de Regresión Lineal
Este algoritmo permite encontrar de forma automática los parámetros de la línea recta que mejor se ajusta a un set de datos. Si quieres entender en qúe consiste este algoritmo, te sugiero revisar el artículo en donde explico la Regresión Lineal en detalle.
El set de datos
Los datos a usar en este tutorial corresponden a la medición de la presión sanguínea sistólica (medida en mm de Mercurio) para 29 sujetos de diferentes edades.
En este set de datos la variable independiente (x) corresponde a la edad de cada sujeto, mientras que la variable dependiente (y) es precisamente la presión sanguínea.
La figura de abajo muestra la relación entre estas dos variables, evidenciando que los datos tienen un comportamiento lineal:
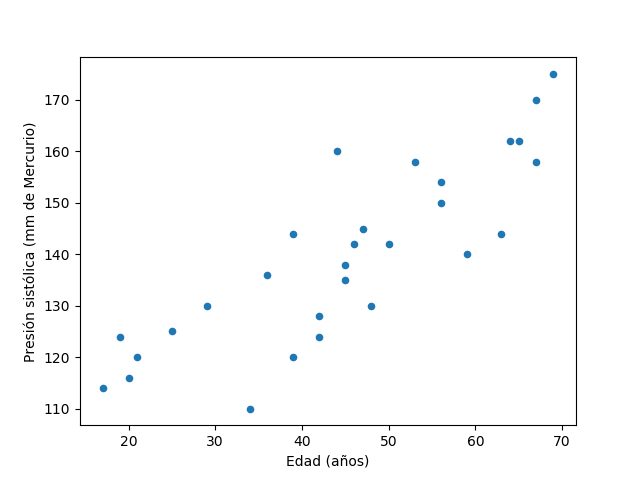
A continuación veremos cómo implementar la Regresión Lineal en Python para encontrar los parámetros de la línea recta que mejor se ajusta a estos datos.
Librerías requeridas
Para la implementación de este algoritmo se requieren tres librerías:
- Pandas: que permite leer el set de datos, almacenado en formato .csv (comma separated values)
- Numpy: usado para almacenar los datos x y y, así como para implementar de manera sencilla las funciones para el cálculo del error y el gradiente descendente.
- Matplotlib: para graficar los resultados del algoritmo.
Estas librerías se pueden importar en Python usando las siguientes líneas de código:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Funciones auxiliares
Se implementarán tres funciones que en conjunto permiten realizar la regresión lineal de los datos.
El modelo: calcular_modelo
Esta función permite calcular cada uno de los datos resultantes de la regresión, y corresponde a la ecuación:
$\hat{y}_i = wx_i + b$
donde w y b son los parámetros que queremos calcular con el algoritmo de Regresión Lineal.
Ésta es la implementación en Python:
def calcular_modelo(w,b,x):
'''Retorna el valor w*x+b correspondiente al modelo lineal'''
return w*x+b
El error cuadrático medio: calcular_error
En la explicación de la Regresión Lineal vimos que la pérdida o función de error a usar será el error cuadrático medio (ECM), que obedece a la siguiente ecuación:
$ECM = \displaystyle \frac{1}{N} \sum_{i=1}^{N}\left(y_i-\hat{y}_i\right)^2$
donde N es el número total de datos (en este caso igual a 29, que es el número total de sujetos).
Por lo tanto, el código correspondiente en Python es el siguiente:
def calcular_error(y,y_):
'''Calcula el error cuadrático medio entre el dato original (y)
y el dato generado por el modelo (y_)'''
N = y.shape[0]
error = np.sum((y-y_)**2)/N
return error
Algoritmo del Gradiente Descendente: gradiente_descendente
El algoritmo del Gradiente Descendente permite actualizar los valores w y b haciendo uso de las derivadas del ECM.
Estas derivadas se calculan usando las siguientes ecuaciones:
$$dw = \displaystyle -\frac{2}{N} \sum_{i=1}^{N}x\left(y_i-wx_i-b\right)$$
$$db = \displaystyle -\frac{2}{N} \sum_{i=1}^{N}\left(y_i-wx_i-b\right)$$
donde N nuevamente corresponde a la cantidad total de datos (29).
Los parámetros w y b se actualizan usando las siguientes fórmulas:
$$w \leftarrow w - \alpha dw$$
$$b \leftarrow b - \alpha db$$
donde α representa la tasa de aprendizaje.
Así, para la implementación de la función usamos el siguiente código:
def gradiente_descendente(w_, b_, alpha, x, y):
'''Algoritmo del gradiente descendente para minimizar el error
cuadrático medio'''
N = x.shape[0] # Cantidad de datos
# Gradientes: derivadas de la función de error con respecto
# a los parámetros "w" y "b"
dw = -(2/N)*np.sum(x*(y-(w_*x+b_)))
db = -(2/N)*np.sum(y-(w_*x+b_))
# Actualizar los pesos usando la fórmula del gradiente descendente
w = w_ - alpha*dw
b = b_ - alpha*db
return w, b
Por tanto, una vez implementadas las funciones auxiliares, podemos realizar la lectura de los datos y el entrenamiento del modelo, descritos a continuación.
Lectura de los datos
El set de datos se almacenará en un DataFrame de Pandas, y posteriormente las variables edad y presión sanguínea se almacenan en dos arreglos Numpy (x y y respectivamente):
datos = pd.read_csv('dataset.csv', sep=",", skiprows=32, usecols=[2,3])
x = datos['Age'].values
y = datos['Systolic blood pressure'].values
A continuación veamos cómo realizar el entrenamiento del modelo.
Entrenamiento usando el Gradiente Descendente
Ahora usamos las tres funciones definidas anteriormente para implementar la regresión lineal en Python, logrando así que el modelo “aprenda” los parámetros w y b.
Para ello inicializamos de forma aleatoria dichos parámetros:
np.random.seed(2)
w = np.random.randn(1)[0]
b = np.random.randn(1)[0]
donde `np.random.seed(2) se usa para poder replicar los resultados incluso si el algoritmo se ejecuta en diferentes computadores.
Posteriormente definimos los parámetros α (tasa de aprendizaje) y el número de iteraciones. Teniendo en cuenta que se tienen tan solo 29 datos, la tasa de aprendizaje es relativamente pequeña (0.0004) para garantizar la convergencia del algoritmo; lo anterior implica que se requerirá un número de iteraciones relativamente alto (40000 en este caso):
alpha = 0.0004
nits = 40000
Para aprender los parámetros w y b se llevan a cabo los siguientes pasos dentro de cada iteración:
- Actualizar los parámetros usando la función
gradiente_descendente - Calcular la regresión lineal $\hat{y}_i$ usando la función
calcular_modelo - Actualizar el valor del ECM usando la función `calcular_error
- Imprimir los resultados en pantalla
Por tanto, el código completo para esta Regresión Lineal en Python es el siguiente:
error = np.zeros((nits,1))
for i in range(nits):
# Actualizar valor de los pesos usando el gradiente descendente
[w, b] = gradiente_descendente(w,b,alpha,x,y)
# Calcular el valor de la predicción
y_ = calcular_modelo(w,b,x)
# Actualizar el valor del error
error[i] = calcular_error(y,y_)
# Imprimir resultados cada 1000 epochs
if (i+1)%1000 == 0:
print("Epoch {}".format(i+1))
print(" w: {:.1f}".format(w), " b: {:.1f}".format(b))
print(" error: {}".format(error[i]))
print("=======================================")
Veamos ahora los resultados de llevar a cabo esta Regresión Lineal.
Resultados
En primer lugar, obtengamos la gráfica del ECM vs. las iteraciones:
plt.plot(range(nits),error)
plt.xlabel('epoch')
plt.ylabel('ECM')
plt.show()
Al observar la figura de abajo podemos confirmar que la pérdida (ECM) disminuye a medida que el número de iteraciones se incrementa:
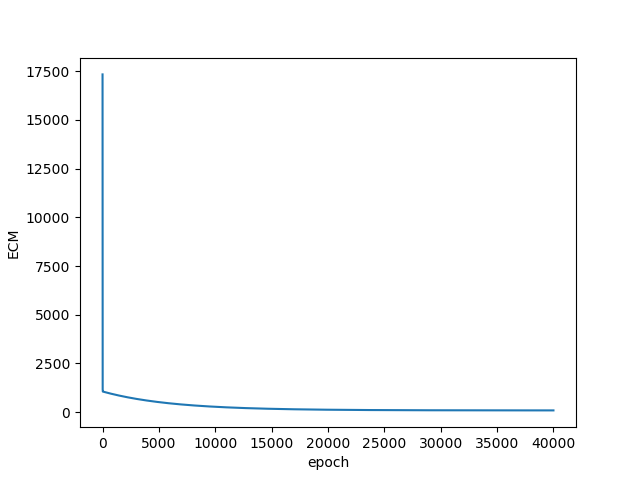
Ahora veamos el resultado de la Regresión Lineal y cómo después del entrenamiento obtenemos una línea recta que se ajusta bastante bien a los datos reales:
y_regr = calcular_modelo(w,b,x)
plt.scatter(x,y)
plt.plot(x,y_regr,'r')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Al ejecutar las anteriores líneas de código, se obtiene el siguiente resultado:
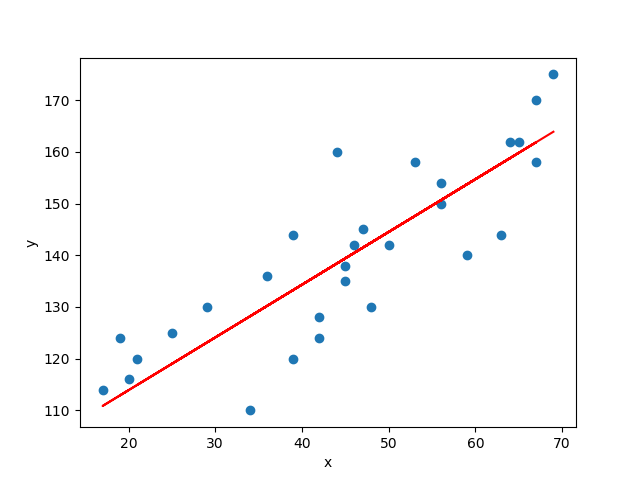
El resultado de la Regresión Lineal (línea de color rojo) permite evidenciar que ésta se ajusta bastante bien a los datos originales (puntos azules), lo cual permite verificar que el algoritmo de Regresión Lineal en Python funciona adecuadamente.
Por último, veamos cómo calcular una predicción a partir del modelo ya entrenado.
Predicción
Para finalizar, podemos realizar una predicción teniendo el modelo ya entrenado.
Si, por ejemplo, queremos conocer el nivel de presión sanguínea que tendrá una persona de 90 años, simplemente ejecutamos las siguientes líneas de código:
edad = 90
presion = calcular_modelo(w,b,edad)
print("A los {}".format(edad), " años se tendrá una presión sanguínea de {:.1f}".format(presion))
Código fuente y set de datos
En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: