La Convolución en las Redes Convolucionales
En este segundo post de la serie “Redes Convolucionales” hablaremos precisamente de la convolución, que le da el nombre a estas redes. Veremos qué es un filtro o kernel, para qué sirve y como a través de la convolución este filtro permite extraer características de una imagen en escala de gris o a color.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Intuición acerca de la convolución
Supongamos que tenemos una imagen como la mostrada en la figura de abajo, y que para una cierta aplicación queremos determinar la presencia únicamente de las líneas verticales:

La anterior imagen está en escala de grises, lo cual quiere decir que cada pixel se representa con un valor entero que está entre 0 y 255. Así, una tonalidad oscura (el fondo de la imagen) se representa con valores cercanos a 0, una tonalidad gris con valores intermedios (cercanos a 128), y una tonalidad clara o brillante (en este caso las líneas) con valores cercanos a 255.
Para poder detectar de forma automática las líneas verticales podemos usar un filtro (o kernel) similar al mostrado en la figura de abajo. Observamos que los valores de cada pixel en este kernel están orientados verticalmente, lo que permitirá posteriormente encontrar el patrón que estamos buscando en la imagen original (las líneas verticales):
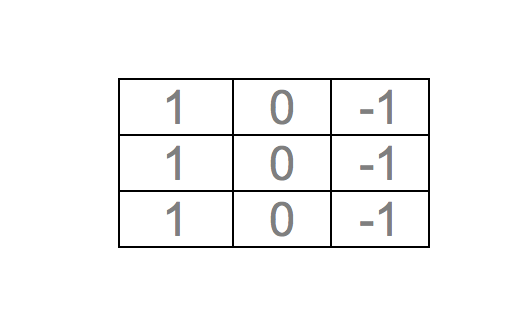
Si realizamos la convolución entre la imagen original y el kernel, entonces obtendremos un resultado similar al mostrado en la siguiente figura:
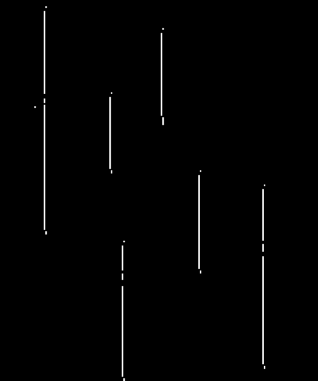
Podemos observar que la imagen resultante contiene únicamente las líneas que queríamos detectar. Así, podemos concluir que la convolución es una operación entre una imagen y un kernel, a través de la cual resulta posible detectar patrones en la imagen. A la entrada requiere una imagen y un kernel, y a la salida genera otra imagen que, idealmente, contendrá las características de interés.
Veamos ahora sí en detalle en qué consiste la Convolución, aplicada por el momento a imágenes en escala de gris.
La convolución en dos dimensiones: explicación detallada
En la figura de abajo se muestra en detalle una imagen en escala de grises y el kernel. La primera tiene un tamaño de 6x6 (es decir dos dimensiones), mientras que el kernel tiene un tamaño de 3x3:
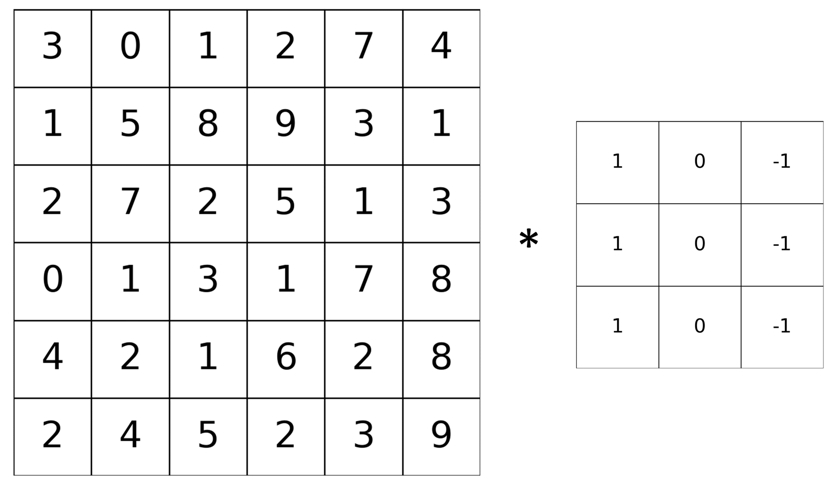
La convolución es un procedimiento iterativo, y a continuación veremos cómo se desarrolla paso a paso.
Primera iteración
En la primera iteración se lleva a cabo el siguiente procedimiento:
- Se ubica el kernel en la esquina superior izquierda de la imagen
- Posteriormente se realiza la multiplicación término a término entre los coeficientes del kernel y los valores de la imagen que se encuentran superpuestos
- El valor correspondiente en la imagen de salida es el resultado de sumar los valores resultado de la multiplicación realizada en el paso anterior.
Esta primera iteración se ilustra en la siguiente figura:
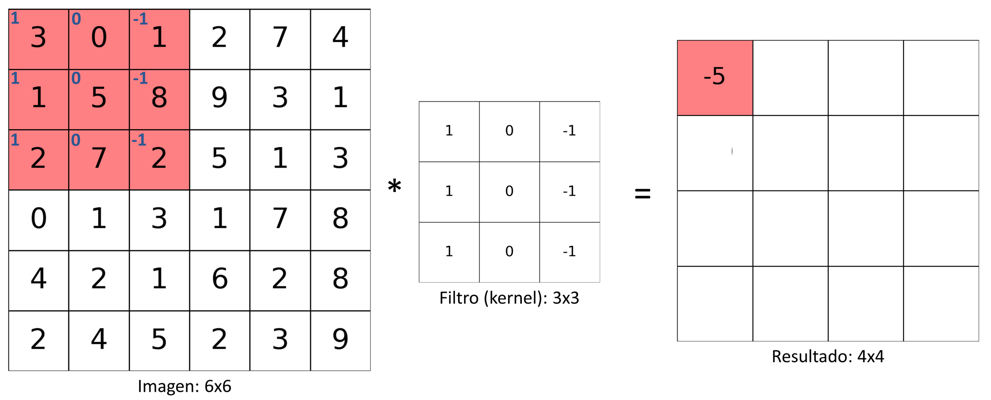
Por tanto, como se describe en el procedimiento anterior, para esta primera iteración el valor resultante de la convolución será igual a multiplicar uno a uno los valores de la imagen y el kernel, y luego sumar el resultado:
$$3\cdot1 + 0\cdot0 + (-1)\cdot1 + 1\cdot1 + 0\cdot5 +$$ $$(-1)\cdot8 + 1\cdot2 + 0\cdot7 + (-1)\cdot2$$ $$ = 3 + 0 -1 + 1 + 0 -8 + 2 + 0 – 2 = -5$$
Segunda iteración
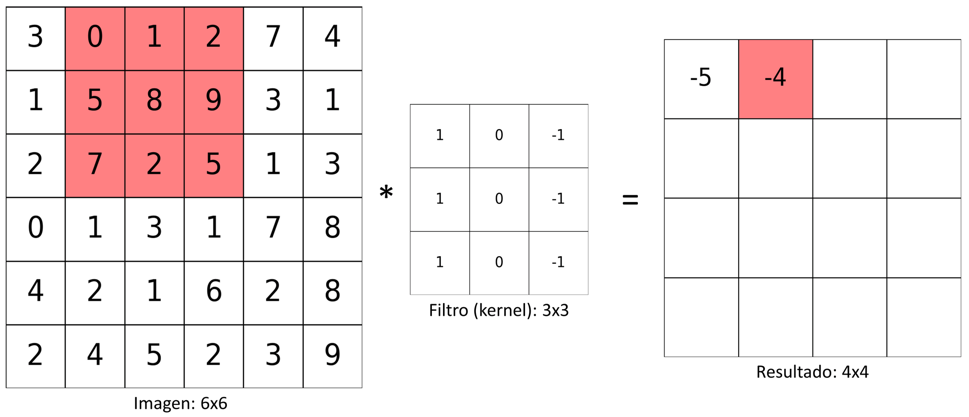
La segunda iteración es casi idéntica a la primera, con la única diferencia de que el kernel se desplaza una posición a la derecha. Así, el procedimiento paso a paso es el siguiente:
- Desplazar el kernel una posición a la derecha
- Repetir los pasos (1) a (3) usados en la primera iteración.
Este procedimiento se muestra a continuación:
Tercera iteración y siguientes
El procedimiento anterior se repite hasta que el kernel llega al extremo derecho de la imagen. Una vez se cumple con esta condición, el kernel se desplaza nuevamente al extremo izquierdo de la imagen y una posición hacia abajo.
El procedimiento se repite hasta que el kernel se haya desplazado por la totalidad de la imagen. En la figura de abajo se muestra el resultado de la última iteración:
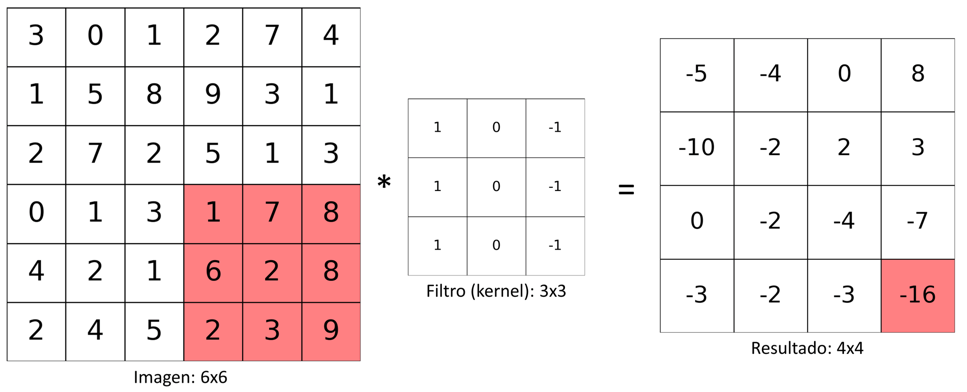
La imagen resultante
En la figura anterior vimos que la imagen de entrada tenía un tamaño de 6x6, el kernel un tamaño de 3x3 y la imagen resultante un tamaño de 4x4.
Teniendo en cuenta lo anterior, podemos concluir que, para una imagen de entrada de m (filas) x n (columnas) y un kernel de tamaño u (filas) x v (columnas), la imagen resultante tendrá m-u+1 (filas) x n-v+1 (columnas).
La convolución 3D o en más dimensiones
La convolución en tres dimensiones es simplemente la convolución aplicada a imágenes en color (RGB, con tres planos de color) o imágenes con múltiples planos de información (más de 3).
Una imagen RGB es similar a una imagen en escala de grises (cada pixel es representado con un valor entre 0 y 255), con una diferencia importante: en lugar de un plano, la imagen RGB contiene tres planos (uno por cada color: R –rojo-, G – verde-, B –azul-), como se muestra en la siguiente figura:
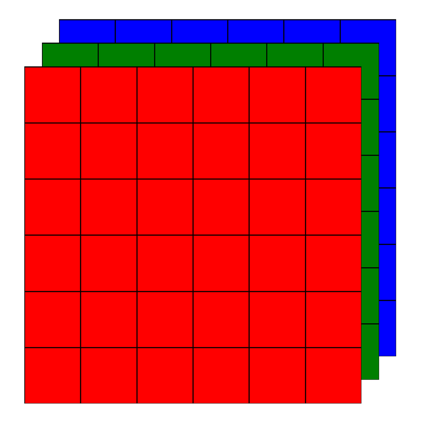
Para este tipo de imágenes (con tres o más planos de información) el algoritmo de la convolución es similar al descrito anteriormente, con dos diferencias importantes:
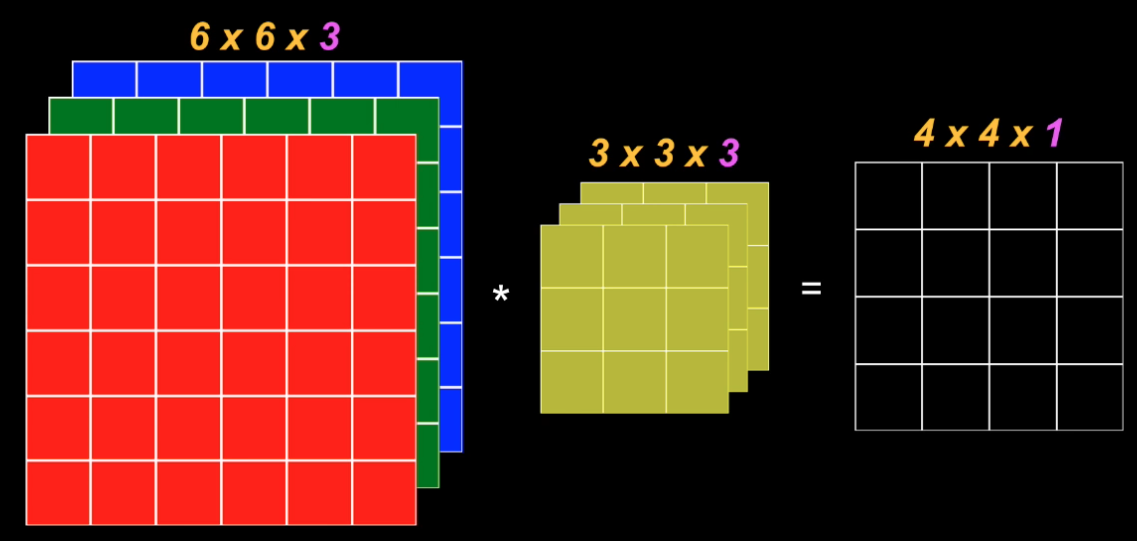
- El kernel contendrá ahora el mismo número de planos de la imagen de entrada (uno por cada canal de la imagen de entrada). Es decir que si queremos procesar una imagen RGB (a color), con un tamaño de 6 (filas) x 6 (columnas) x 3 (planos de color), entonces por ejemplo podemos usar un kernel de 3 (filas) x 3 (columnas) x 3 (planos):
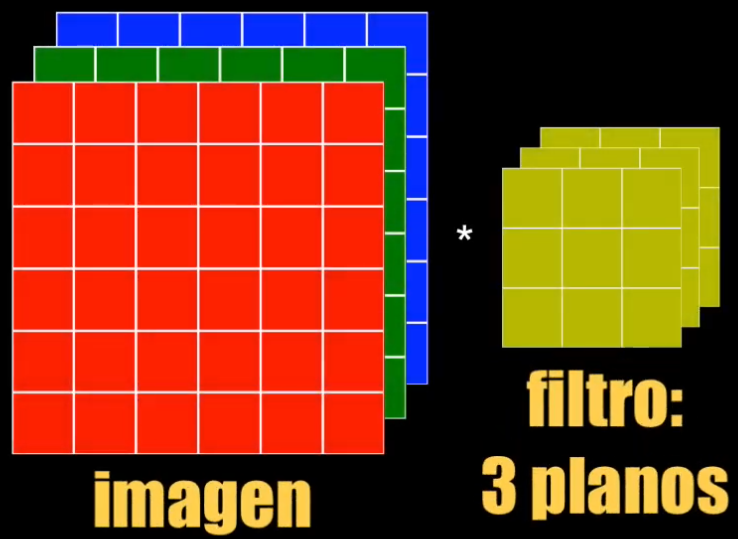
- En cada iteración se convoluciona cada plano del kernel con el correspondiente plano en la imagen de color
- Los resultados de estas convoluciones se suman generando un único valor
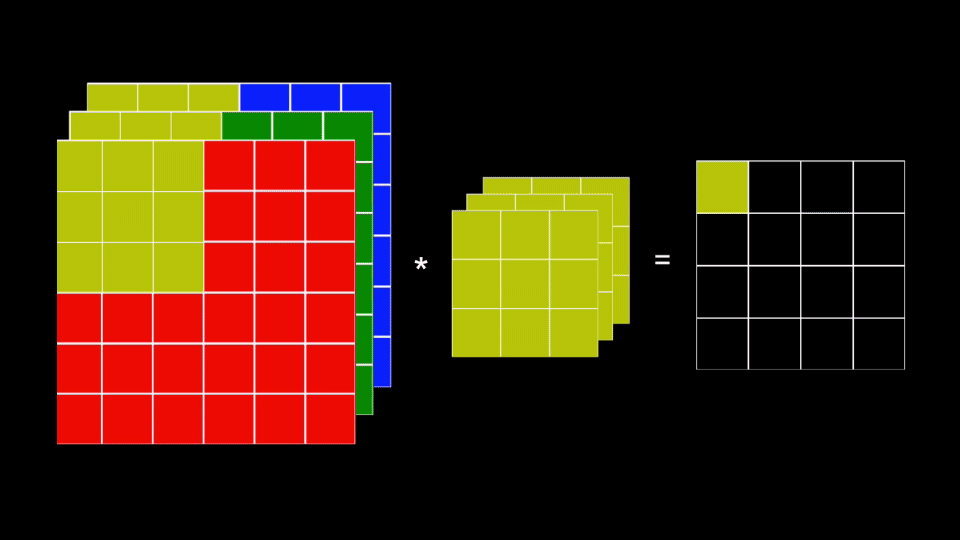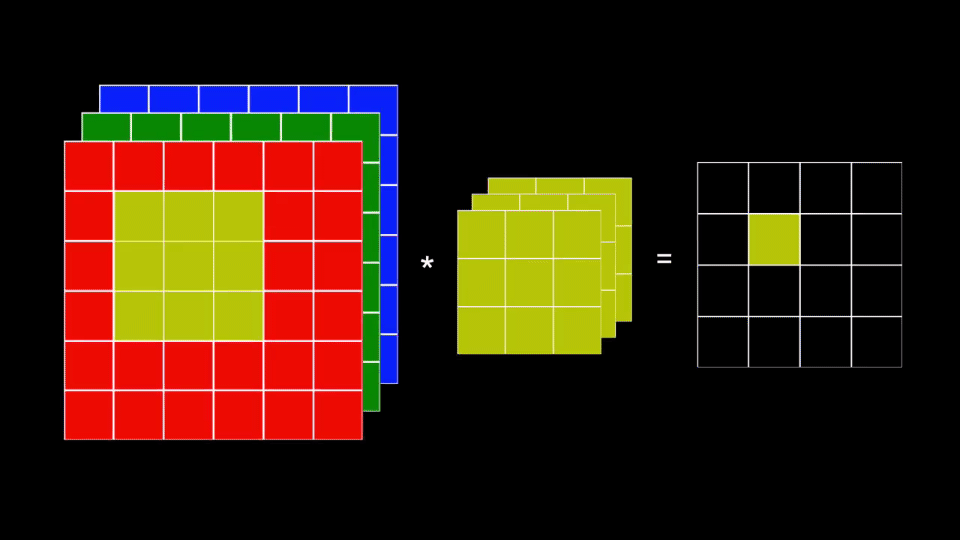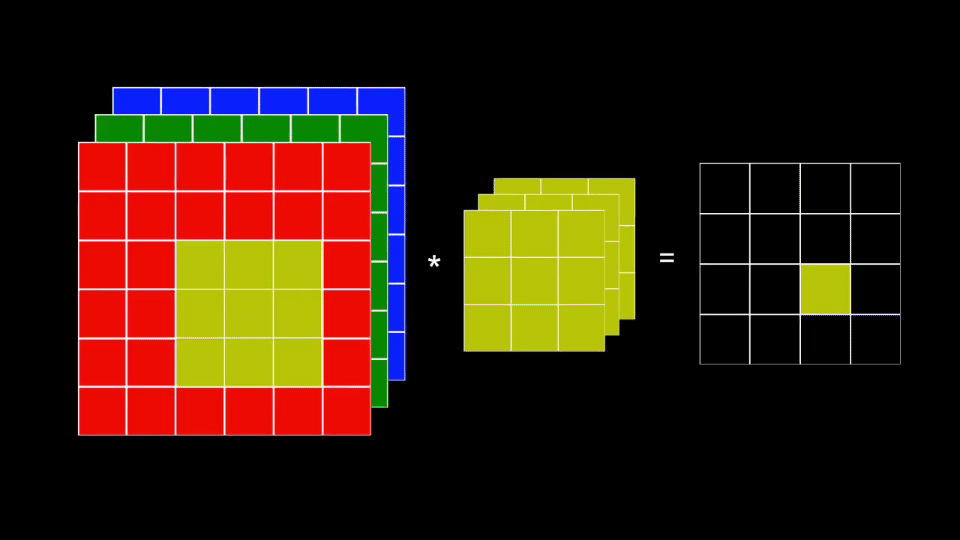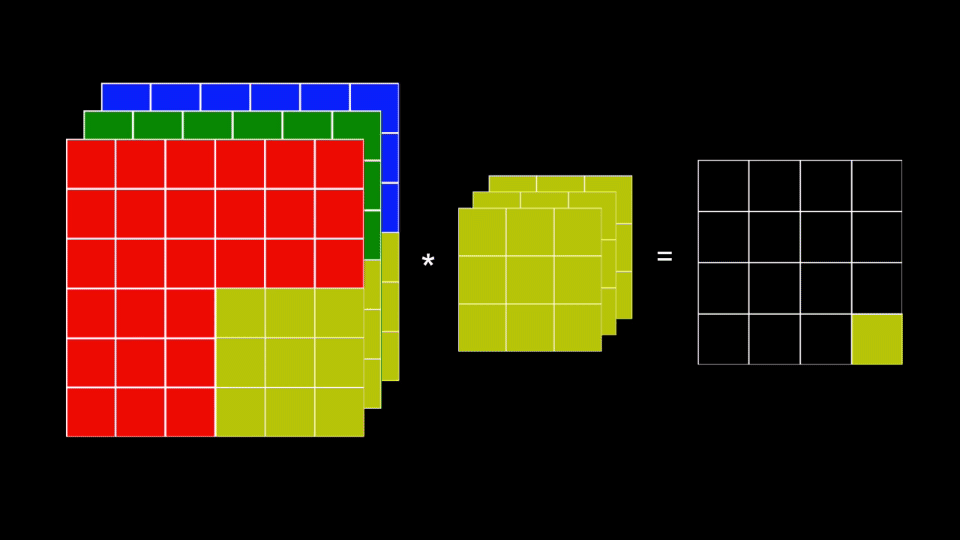
El último paso implica que la imagen resultante siempre contendrá un único plano de información.
Al igual que en el caso de la convolución 2D, en este caso la imagen resultante tendrá un tamaño inferior a la imagen original: m-u+1 x n-v+1, en donde $m$ y $n$ son el número de filas y columnas de la imagen de entrada, y $u$ y $v$ el tamaño del kernel. De nuevo, es importante recordar que la imagen resultante tendrá sólo un plano de información:
Conclusión
En resumen hemos visto que la convolución es una operación que nos permite extraer características de una imagen, para lo cual hace uso de un filtro o kernel, el cual está diseñado específicamente para extraer las características que resulten de mayor interés en la imagen.
Como vimos en el primer post de esta serie, en donde vimos qué son las Redes Convolucionales, los coeficientes de los filtros se obtienen a partir del entrenamiento mismo de la Red Convolucional.
Te invito además a revisar los demás posts de esta serie:
- Padding, strides, max-pooling y stacking en las Redes Convolucionales
- Clasificación de imágenes con Redes Convolucionales en Python (Tutorial)
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: