¿Qué es la Regresión Multiclase?
La Regresión Multiclase es un algoritmo que permite clasificar datos en tres o más categorías. En este post veremos qué es y cómo funciona este, que es uno de los algoritmos básicos del Machine Learning.
Al final de artículo habrás aprendido:
- Qué es y en qué casos se usa el algoritmo de Regresión Multiclase
- Cómo funciona, paso a paso, el algoritmo
- Qué es la función de activación softmax
- Semejanzas y diferencias con respecto al algoritmo de Regresión Logística
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
¿Qué es la Regresión Multiclase?
La Regresión Multiclase es un algoritmo de Machine Learning que permite realizar la clasificación de datos cuando existen tres o más categorías.
Por ejemplo, en un cliente de correo electrónico, la regresión multiclase permitiría clasificar un mensaje entrante como spam, uno proveniente del trabajo, de redes sociales o de un amigo o familiar.
Veamos en detalle el funcionamiento de este algoritmo.
Planteamiento del problema
Supongamos que se tienen 90 datos X, cada uno representado con dos características ($x_1$, $x_2$) y perteneciente a una de tres posibles categorías Y: “0”, “1” ó “2”. Un ejemplo de este set de datos se ilustra en la siguiente figura:
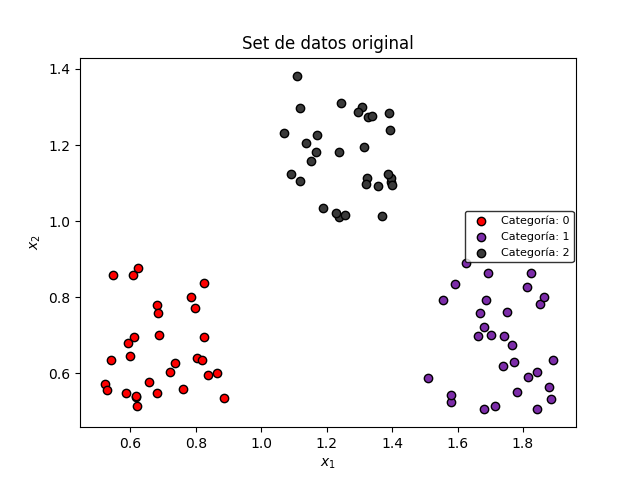
Podemos observar que estos puntos se encuentran distribuidos en tres agrupaciones, correspondientes a cada una de las tres categorías.
El objetivo de la Regresión Multiclase es entonces clasificar los datos en estas tres categorías, encontrando de forma automática las fronteras de decisión que establecen los límites entre una y otra. Estas fronteras de decisión se muestran como líneas rectas de color azul en la siguiente figura:
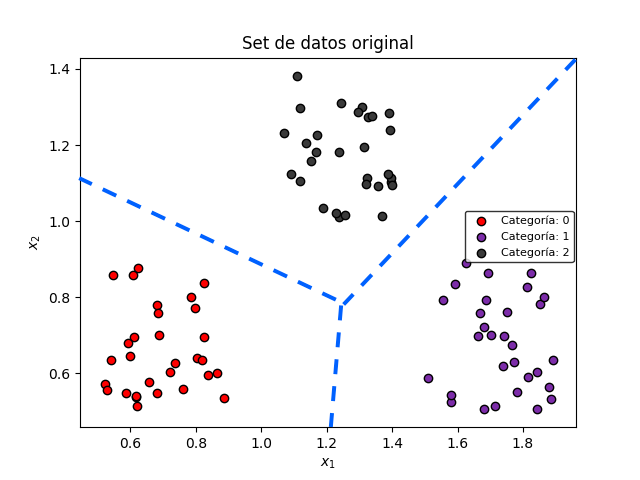
Para obtener las fronteras de decisión el algoritmo de Regresión Multiclase lleva a cabo tres pasos: transformación de los datos de entrada, aplicación de una función de activación y clasificación en una de las tres categorías existentes.
Veamos cómo se llevan a cabo estos procedimientos.
Funcionamiento del algoritmo
El modelo de regresión multiclase tendrá una entrada $\bar{x}$ y una salida $\bar{y}$.
En este caso particular, la entrada es un vector con dos datos ($x_1$, $x_2$) mientras que la salida es un vector con tres elementos, correspondientes a cada una de las categorías resultantes de la clasificación.
La clasificación se da en dos pasos que se resumen en la figura de abajo:
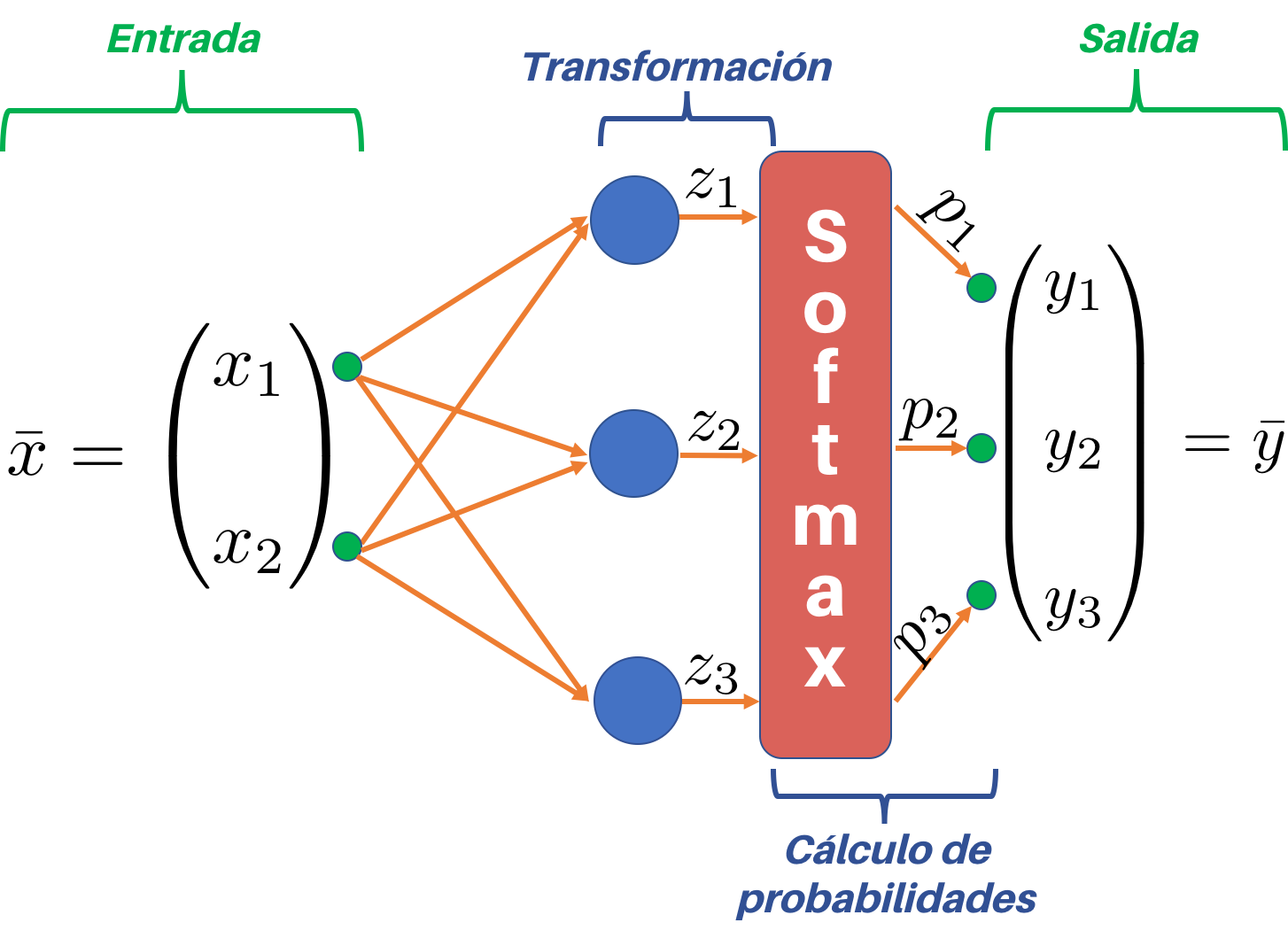
En primer lugar cada una de las características de entrada ($x_1$, $x_2$) es transformada en los datos $z_1$, $z_2$ y $z_3$. Posteriormente se hace uso de la función de activación softmax para calcular tres probabilidades ($p_1$, $p_2$, $p_3$). Finalmente, se determina cuál de las probabilidades es más alta y se asigna entonces la categoría correspondiente.
Así, por ejemplo, si el objeto es clasificado en la categoría 2 entonces el vector de salida tendrá la forma $\bar{y} = (0, 0, 1)$, donde el “1” ubicado en la posición 2 del vector indica precisamente la clase asignada.
Veamos en detalle en qué consisten la transformación de los datos y la función softmax.
Transformación de los datos
Para transformar cada dato de entrada $\bar{x}$ usamos la misma operación definida previamente en la Regresión Logística:
$z_i = \bar{w_i} \cdot \bar{x} + b_i$
donde i = 1, 2, 3 pues se tendrán tres salidas ($z_1$, $z_2$, $z_3$). Cada vector $w_i$ tendrá dos elementos, pues cada dato de entrada contendrá precisamente dos características.
De nuevo, al igual que con la Regresión Logística y la Regresión lineal, los parámetros $\bar{w_i}$ y $b_i$ se aprenden durante el entrenamiento (que explicaremos más adelante).
Función de activación softmax
Para clasificar los datos, primero los tres valores obtenidos tras la transformación son convertidos en probabilidades (cantidades numéricas entre 0 y 1) usando la función softmax, definida como:
$s(p_i) = \frac{e^{z_i}}{\sum_{k=1}^{3}e^{z_k}}$
Esta función permite normalizar las tres probabilidades, garantizando que la suma de las mismas sea igual a 1.0.
Posteriormente, para realizar la clasificación se determina cuál de las tres probabilidades calculadas tiene el valor más alto, que corresponderá a la clase asignada.
Veamos ahora cómo se calculan los parámetros en un modelo de Regresión Multiclase.
Entrenamiento del modelo
Como lo mencionamos anteriormente, el proceso de entrenamiento permite calcular las fronteras de decisión que separan una clase de otra.
Lo anterior equivale a encontrar de forma automática los coeficientes $\bar{w_i}$ y $b_i$ que permiten realizar esta clasificación.
Este entrenamiento es idéntico al procedimiento usado en la Regresión Logística, y consiste en minimizar la entropía cruzada (función de error) usando el método del Gradiente Descendente.
Veamos la manera como las fronteras de decisión se modifican durante el entrenamiento para permitir la clasificación de los datos:
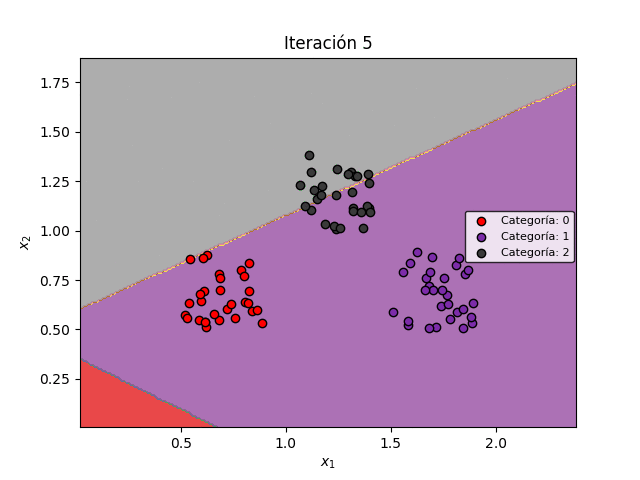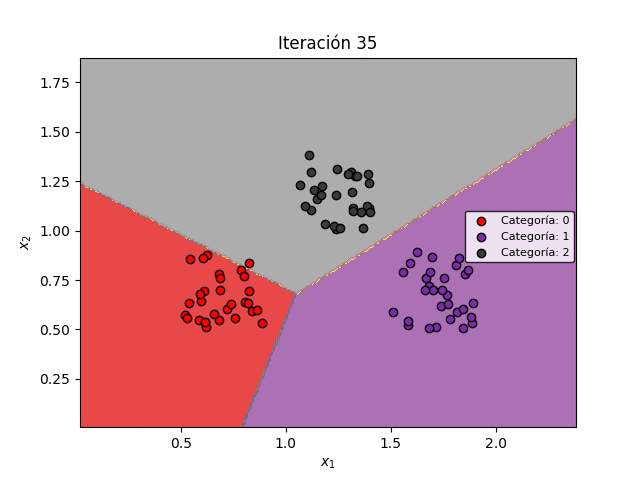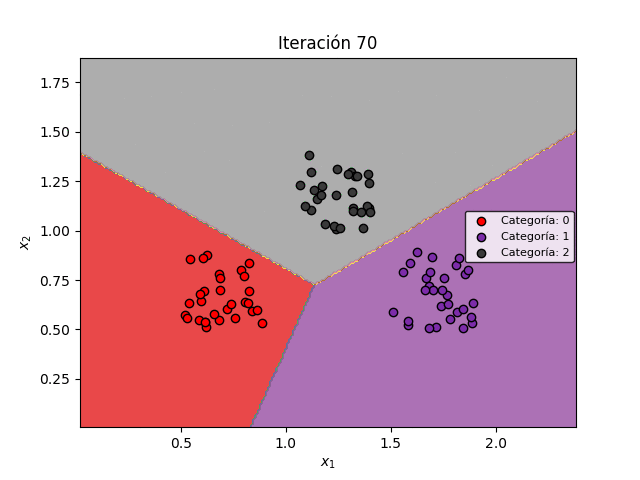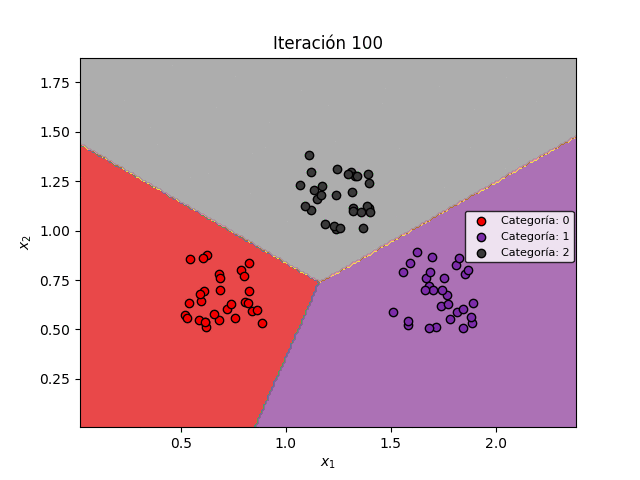
Finalmente, veamos un ejemplo numérico que nos permitirá comprender en detalle el algoritmo de Regresión Multiclase.
Ejemplo numérico
Dato de entrada
Tomemos uno de los 90 datos y clasifiquémoslo ousando el algoritmo de Regresión Multiclase.
Recordemos que se tienen tres categorías: “0”, “1” y “2”. Supongamos que el dato de entrada al modelo pertenece a la categoría “1” y que está dado por los siguientes valores:
$$\bar{x} = \begin{pmatrix} 1.839\ 0.557 \end{pmatrix} $$
Parámetros del modelo
El modelo de Regresión Multiclase tendrá 3 salidas (para cada una de las tres categorías). Además, cada entrada tendrá 2 características. Por tanto, se tendrán que calcular en total:
- Tres parámetros $\bar{w_i}$, pues se tendrán 3 salidas. Cada uno de estos parámetros consiste en un vector con dos elementos, pues el dato de entrada contiene 2 características.
- Tres parámetros $b_i$, uno por cada una de las tres salidas.
Supongamos que una vez realizado el entrenamiento se obtienen estos parámetros:
- Primera salida: $\bar{w_1} = (-1.53, 0.52)$, $b_1 = 2.47$
- Segunda salida: $\bar{w_2} = (2.98, -1.42)$, $b_2 = -1.14$
- Tercera salida: $\bar{w_3} = (-0.12, 3.29)$, $b_3 = -1.33$
Con estos parámetros podemos calcular la transformación de los datos.
Transformación de los datos de entrada
Para ello aplicamos la ecuación vista anteriormente:
$z_i = \bar{w_i} \cdot \bar{x} + b_i$
obteniendo los siguientes resultados:
$$z_1 = \bar{w_1} \cdot \bar{x} + b_1 = (-1.53, 0.52) \cdot \begin{pmatrix} 1.839\ 0.557 \end{pmatrix} + 2.47 = -0.05$$
$$z_2 = \bar{w_2} \cdot \bar{x} + b_2 = (2.98, -1.42) \cdot \begin{pmatrix} 1.839\ 0.557 \end{pmatrix} - 1.14 = 3.55$$
$$z_3 = \bar{w_3} \cdot \bar{x} + b_3 = (-0.12, 3.29) \cdot \begin{pmatrix} 1.839\ 0.557 \end{pmatrix} - 1.33 = 0.27$$
Estos datos aún no han sido normalizados, pues la suma de los tres valores es mayor que 1. Para normalizarlos y obtener las correspondientes probabilidades debemos hacer uso de la función softmax.
Aplicación de la función softmax
Al usar esta función para calcular cada una de las tres probabilidades, obtenemos los siguientes resultados:
$$s(\bar{z}) = \begin{pmatrix} 0.025,\ 0.94,\ 0.035 \end{pmatrix}$$
Se observa que en este caso la suma total de las probabilidades (0.025 + 0.94 + 0.035) es exactamente igual a 1.
Con estas probabilidades es ahora posible realizar la clasificación.
Clasificación del dato
Esta clasificación equivale a determinar en $s(\bar{z})$ la ubicación de la probabilidad más alta, asignando un valor de 1 a esta posición y 0 a las restantes:
$$s(\bar{z}) = \begin{pmatrix} 0.025,\ 0.94,\ 0.035 \end{pmatrix} \rightarrow \bar{y} = \begin{pmatrix} 0,\ 1,\ 0 \end{pmatrix}$$
La primera posición del vector resultante corresponde a la categoría “0”, la segunda a la categoría “1” y la tercera a la categoría “2”. Por tanto, el “1” ubicado en la segunda posición del vector resultante nos indica que el dato ingresado pertenece a la categoría “1”.
Para finalizar, comparemos el algoritmo de Regresión Multiclase con el método de Regresión Logística visto anteriormente.
Semejanzas y diferencias con respecto a la Regresión Logística
- Ambos algoritmos permiten clasificar datos.
- Sin embargo el algoritmo de Regresión Logística contempla únicamente dos posibles categorías, mientras que la regresión multiclase permite clasificar los datos en tres o más categorías.
- Las funciones de activación usadas son no lineales en ambos casos. Para la Regresión Logística se usa la función sigmoidal, mientras que para la Regresión Multiclase se usa la función softmax.
- En ambos casos se usa un proceso de entrenamiento basado en el algoritmo del Gradiente Descendente. Con este entrenamiento es posible aprender los parámetros del modelo.
- Ambos algoritmos usan la misma función de error durante el entrenamiento: la entropía cruzada.
- La principal limitación de los dos algoritmos está en que las fronteras de decisión calculadas son lineales. Así, ninguno de los dos métodos tendrá un desempeño adecuado en la clasificación si los datos a clasificar no son linealmente separables.
Conclusión
En este artículo hemos visto el principio de funcionamiento del algoritmo de Regresión Multiclase. Estos son los elementos más importantes a tener en cuenta:
- La Regresión Multiclase permite clasificar datos en tres o más categorías.
- Para lograrlo realiza primero una transformación de los datos, seguida por el uso de la función softmax y la determinación de la categoría correspondiente a partir de las probabilidades calculadas por esta función.
- La transformación de los datos requiere el cálculo de los parámetros del modelo, obtenida a través del entrenamiento.
- Dicho entrenamiento se lleva a cabo usando el método del Gradiente Descendente que permite minimizar la entropía cruzada.
- Este entrenamiento equivale a encontrar de forma automática las fronteras de decisión que permiten separar las diferentes categorías.
- La principal limitación de este algoritmo es que las fronteras de decisión calculadas son lineales.
- Lo anterior implica que el método se puede usar para clasificar datos siempre y cuando estos sean linealmente separables.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: