La Neurona Artificial y la Regresión Logística
En este post hablaremos de la Neurona Artificial, que es el bloque fundamental de todas las arquitecturas de Redes Neuronales usadas en el Machine Learning. Veremos además cómo esta neurona permite tomar clasificar datos en una de dos posibles categorías, lo que se conoce precisamente como Regresión Logística.
Al final de este artículo habrás aprendido:
- Qué es la Regresión Logística.
- Cuál es el funcionamiento paso a paso de este algoritmo.
- El concepto de Neurona Artificial, bloque elemental de cualquier modelo de Machine Learning.
- Cómo funciona el proceso de entrenamiento en la Regresión Logística.
- Las limitaciones de este algoritmo.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Además, en el siguiente enlace podrás encontrar un tutorial con la implementación de la Regresión Logística en Python y Keras.
¿Qué es la Regresión Logística?
La Regresión Logística es un algoritmo de Machine Learning que permite tomar una serie de datos y clasificarlos en una de dos posibles categorías o clases.
Así, si por ejemplo los datos corresponden al ritmo cardíaco de una persona que puede tener alguna enfermedad, entonces la Regresión Logística permite clasificar a este sujeto como sano o enfermo.
El algoritmo toma como entrada una serie de datos X y genera a la salida una variable Y con uno de dos posibles valores: 0 o 1. A estos valores de salida se les denomina clases o categorías:
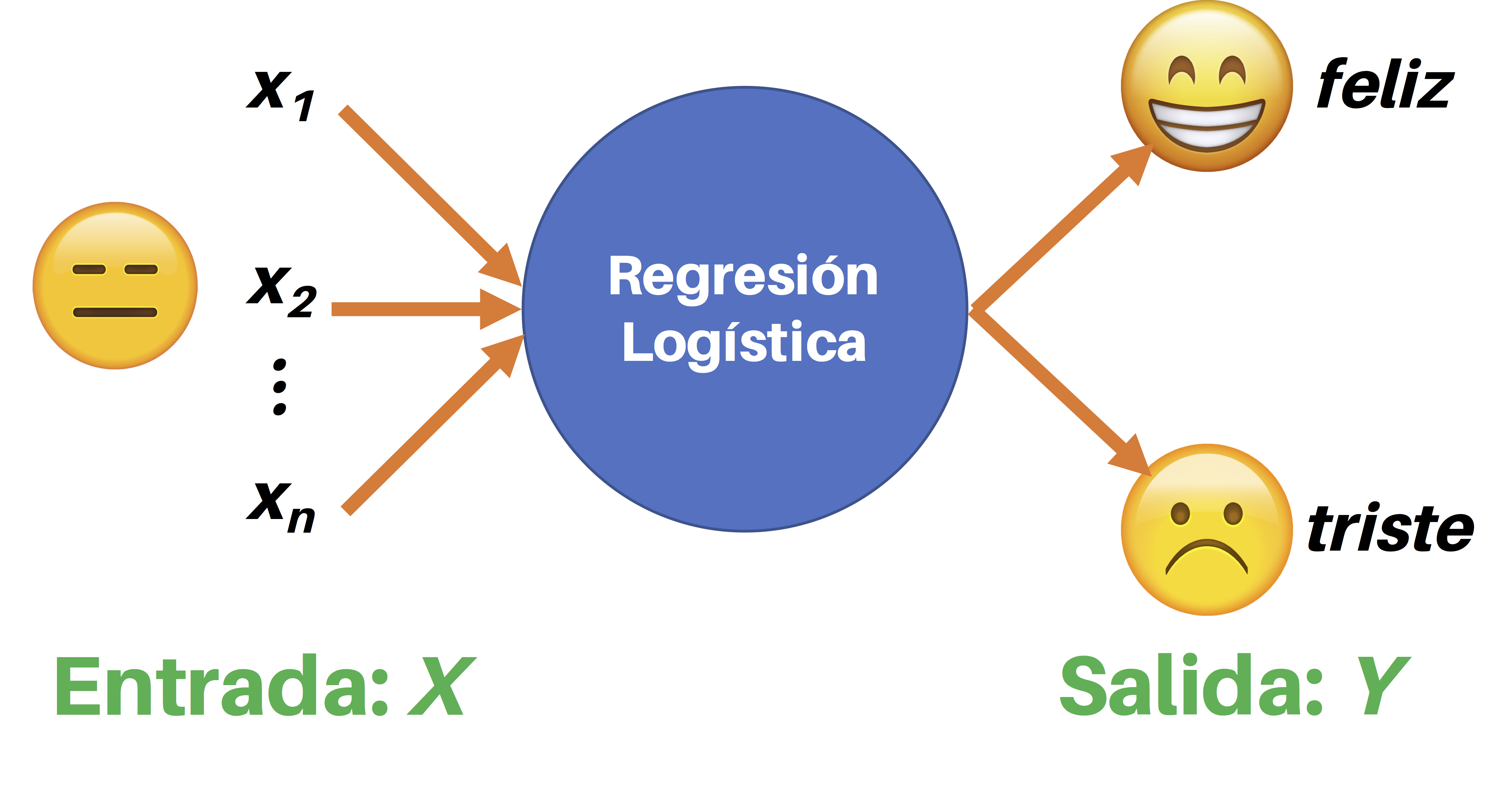
Veamos ahora de forma detallada en qué consiste el algoritmo.
¿Cómo funciona la Regresión Logística?
Para entender el método de la Regresión Logística, definamos inicialmente un problema de aplicación.
El problema
Supongamos que se tiene un set de 100 datos. Cada dato se representa con dos características (dos cantidades numéricas) y además pertenece a una de dos posibles categorías: 0 ó 1. Un ejemplo de este set de datos se muestra en la siguiente tabla:
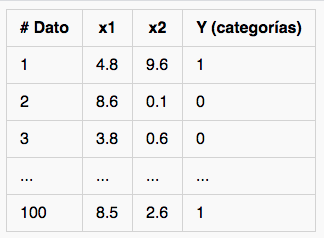
Gráficamente, los 100 datos se encuentran distribuidos de la siguiente manera:
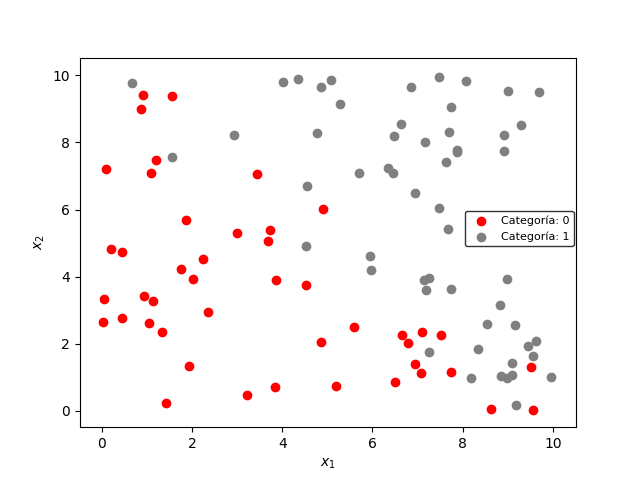
El objetivo de la Regresión Logística es clasificar de forma automática estos datos en las dos categorías existentes. Esto equivale a encontrar una frontera que permita separar los datos en dos agrupaciones diferentes, como se muestra a continuación:
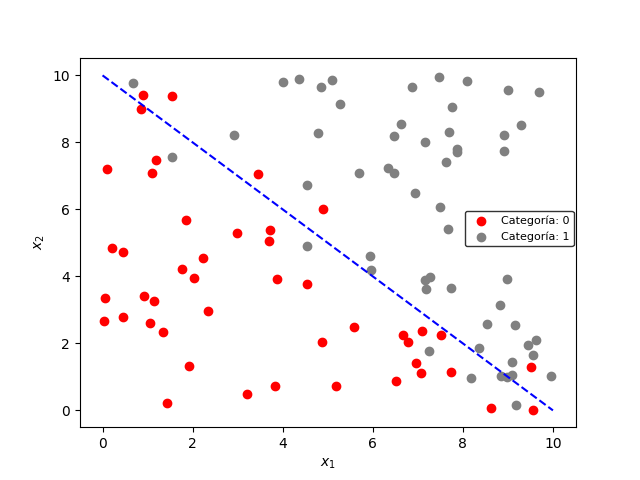
La frontera de decisión
La línea mostrada en la figura anterior se conoce como frontera de decisión, y se puede obtener automáticamente con el algoritmo de Regresión Logística. En la figura, los datos ubicados encima de la frontera serán clasificados como categoría “1”, y los datos ubicados debajo como categoría “0”.
Veamos a continuación el procedimiento que se debe llevar a cabo para determinar esta frontera de decisión.
Transformación de los datos de entrada
Para facilitar el proceso de clasificación es necesario realizar una transformación de los datos de entrada. Esto se logra usando la siguiente ecuación:
$z_i = \vec{w} \cdot \vec{x_i}+b$
donde $\vec{x_i}$ es un vector que contiene dos valores para cada uno de los datos de entrada:
$\vec{x_{i}} = \begin{pmatrix}x_{1_i} \ x_{2_i} \end{pmatrix}$
e i corresponde a cada uno de los 100 datos que se están usando en este caso.
Por su parte, los parámetros $\vec{w}$ y $b$ corresponden a los coeficientes o parámetros del modelo que se obtienen durante el proceso de entrenamiento (el cual analizaremos más adelante).
Con dicha transformación se logra entonces una separación inicial de los datos, para su posterior clasificación.
Esta transformación se representa gráficamente de la siguiente manera:
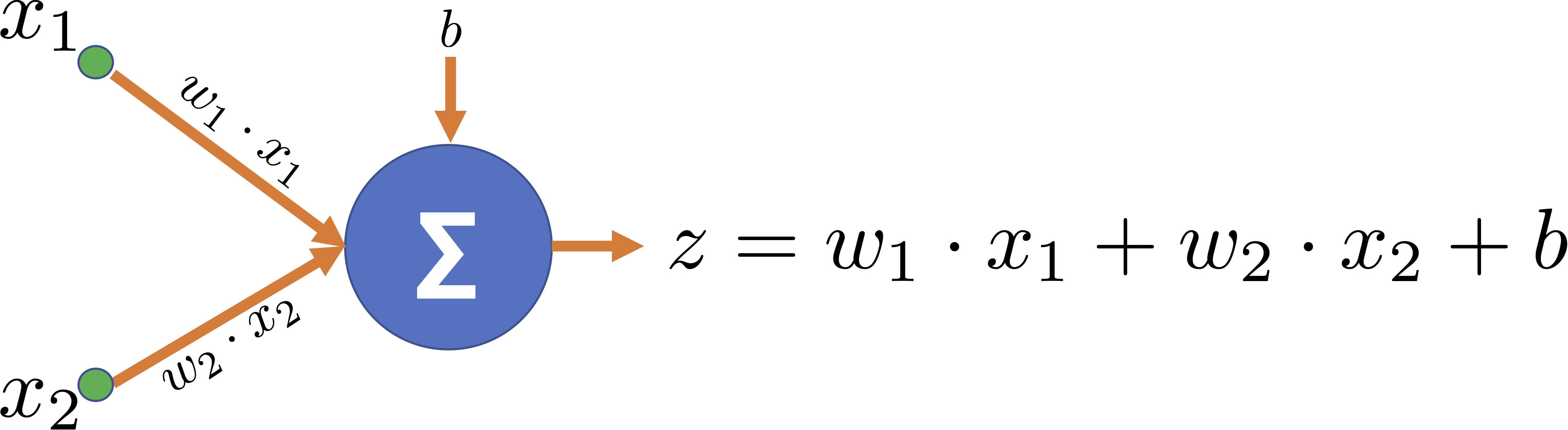
Una vez transformados los datos, el resultado obtenido se lleva a una Función de Activación, explicada a continuación.
La Función de Activación
Los datos transformados ($z_i$) tienen un rango continuo de valores. Sin embargo, para el proceso de clasificación se requiere un rango discreto (0 ó 1, es decir sólo uno de dos posibles valores), el cual se puede obtener con la función de activación.
Esta función tiene un comportamiento no lineal, y en el caso de la Regresión Logística se usa la función sigmoidal mostrada a continuación:
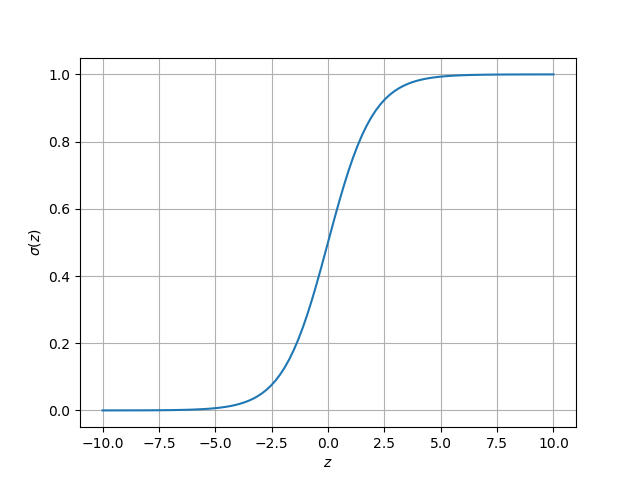
que puede ser calculada a través de la siguiente ecuación:
$\sigma(z) = \frac{1}{1+e^{-z}}$
Se observa que la entrada (z) puede tener cualquier valor tanto positivo como negativo. Sin embargo, la salida siempre estará en el rango de 0 a 1.
La función sigmoidal entrega entonces una probabilidad (en el rango de 0 a 1) de que el dato de entrada pertenezca a alguna de las dos categorías.
A continuación veremos un ejemplo numérico que permitirá entender el proceso de clasificación.
Un ejemplo numérico
Tomemos el siguiente dato de entrada:
$\vec{x_{1}} = \begin{pmatrix}x_{1_1} \ x_{2_1} \end{pmatrix} = \begin{pmatrix}4.86 \ 9.64 \end{pmatrix}$
que pertenece a la clase “1”. Supongamos que después del proceso de entrenamiento, los parámetros calculados para el modelo son los siguientes:
$\vec{w} = \begin{pmatrix} 0.8, 0.6\end{pmatrix}$
$b = -7$
Al aplicar la transformación definida anteriormente, obtendremos:
$z_1 = \vec{w} \cdot \vec{x_1}+b$ $z_1 = \begin{pmatrix} 0.8, 0.6\end{pmatrix} \cdot\begin{pmatrix}4.86 \ 9.64 \end{pmatrix}-7$ $z_1 = 0.8 \cdot 4.86 + 0.6 \cdot 9.64 - 7 = 2.67$
Si ahora aplicamos la función sigmoidal a este valor, obtenemos el siguiente resultado:
$\sigma(z_{1}) = \frac{1}{1+e^{-2.67}} = 0.93$
La probabilidad obtenida (0.93) es más cercana a 1 que a 0 y por tanto el resultado nos indica que el dato $\vec{x_1}$ será clasificado en la categoría “1”.
Para el dato $\vec{x_2}$, que pertenece a la clase “0”:
$\vec{x_{2}} = \begin{pmatrix}x_{1_2} \ x_{2_2} \end{pmatrix} = \begin{pmatrix}8.6 \ 0.05 \end{pmatrix}$
se obtendrá la siguiente clasificación usando el mismo procedimiendo descrito anteriormente:
$z_2 = -0.07$
$\sigma(z_2) = 0.48$
La probabilidad obtenida (0.48) es más cercana a 0 que a 1, indicando así que el dato $x_2$ pertenece a la categoría “0”.
Hemos visto que la Regresión Logística involucra dos operaciones básicas: transformación de los datos y aplicación de la función de activación. Estos dos procedimientos se pueden agrupar en un elemento conocido como Neurona Artificial, la cual definimos a continuación.
La Neurona Artificial: el elemento esencial de cualquier Red Neuronal
Una Neurona Artificial es una unidad algorítmica que toma un dato (vector) de entrada $\vec{x}$ y que genera un vector de salida $\vec{y}$ llevando a cabo las siguientes operaciones:
- Transformación de $\vec{x}$ usando la ecuación:
$z = \vec{w} \cdot \vec{x}+b$
- Aplicación de una función de activación no lineal, que en el caso de la Regresión Logística corresponde a la función sigmoidal.
Los elementos que conforman a esta neurona se ilustran a continuación:
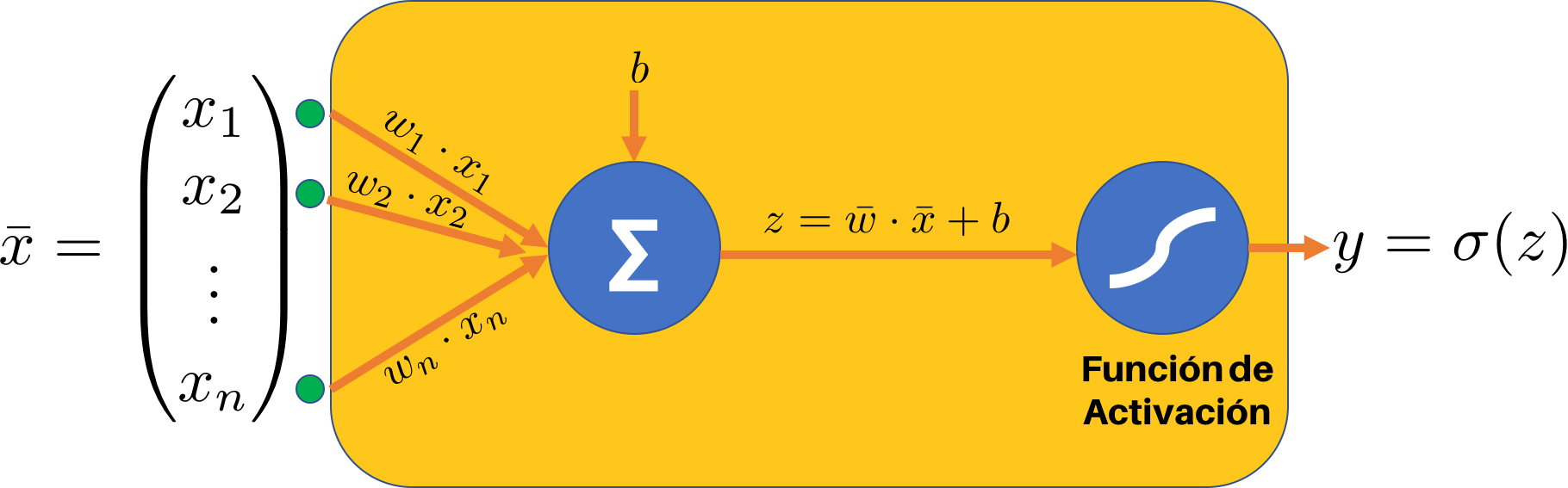
La Neurona Artificial es el bloque fundamental de todos los modelos de Deep Learning existentes en la actualidad, y por ello resulta importante tener claros los conceptos de transformación y función de activación.
Veamos ahora cómo se lleva a cabo el entrenamiento en la Regresión Logística.
Entrenamiento del modelo en la Regresión Logística
En el caso de la Regresión Lineal vimos que el entrenamiento permitía aprender los parámetros del modelo. En dicho procedimiento se llevaban a cabo los siguientes pasos:
- Definición de la función de error.
- Inicialización aleatoria de los parámetros del modelo.
- Definición de la tasa de aprendizaje y el número de iteraciones.
- Actualización de los parámetros del modelo usando el algoritmo del Gradiente Descendente.
Así, este proceso de entrenamiento consistía en aplicar un algoritmo de optimización (el Gradiente Descendente) para calcular los parámetros del modelo que minimizan la pérdida.
En la Regresión Logística se siguen estos mismos cuatro pasos. La única diferencia radica en el hecho de que la función de error usada ya no es el error cuadrático medio sino la entropía cruzada, discutida a continuación.
La función de error en la Regresión Logística
La pérdida o error es una cantidad numérica que mide la diferencia existente entre las categorías a las que realmente pertenece cada uno de los datos (0 o 1, y que en adelante llamaremos $y$) y las que se obtienen durante el entrenamiento del modelo (que llamaremos $\hat{y}$).
Para la Regresión Logística no usamos el error cuadrático medio, pues al ser $y$ y $\hat{y}$ variables binarias, obtendríamos una función con múltiples mínimos como la mostrada a continuación:
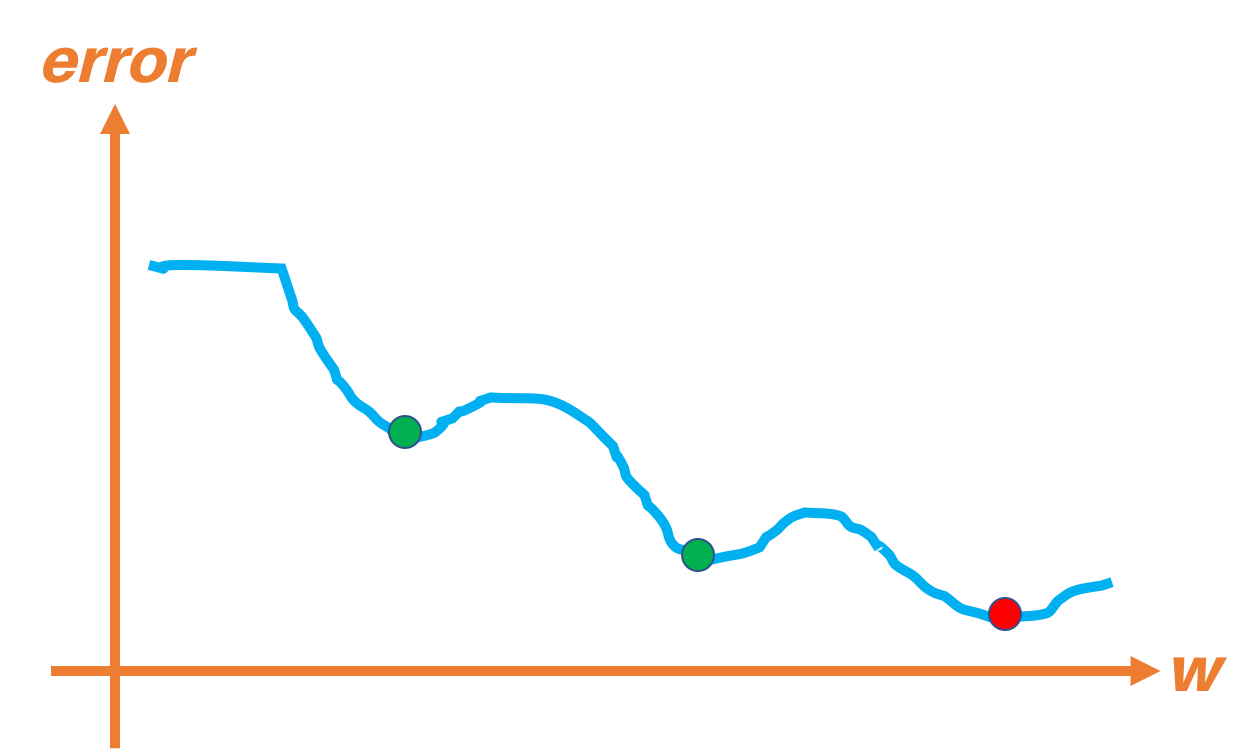
Al tener múltiples mínimos es muy probable que el algoritmo del Gradiente Descendente no se detenga en el mínimo absoluto de la función sino que lo haga en un mínimo local. Esto haría que el entrenamiento no resultase adecuado.
Por tanto, en el caso de la Regresión Logística se usa una función de pérdida conocida como la entropía cruzada (cross-entropy) que se define matemáticamente como:
$\displaystyle error = -\frac{1}{N} \sum_{i=1}^N \left[ y_i \cdot ln\hat{y_i}+(1-y_i) \cdot ln(1-\hat{y_i}) \right]$
donde N representa el número total de datos usados en la regresión, y ln es la función logaritmo natural.
El uso de la entropía cruzada garantiza que la pérdida tendrá un único mínimo como se muestra a continuación:
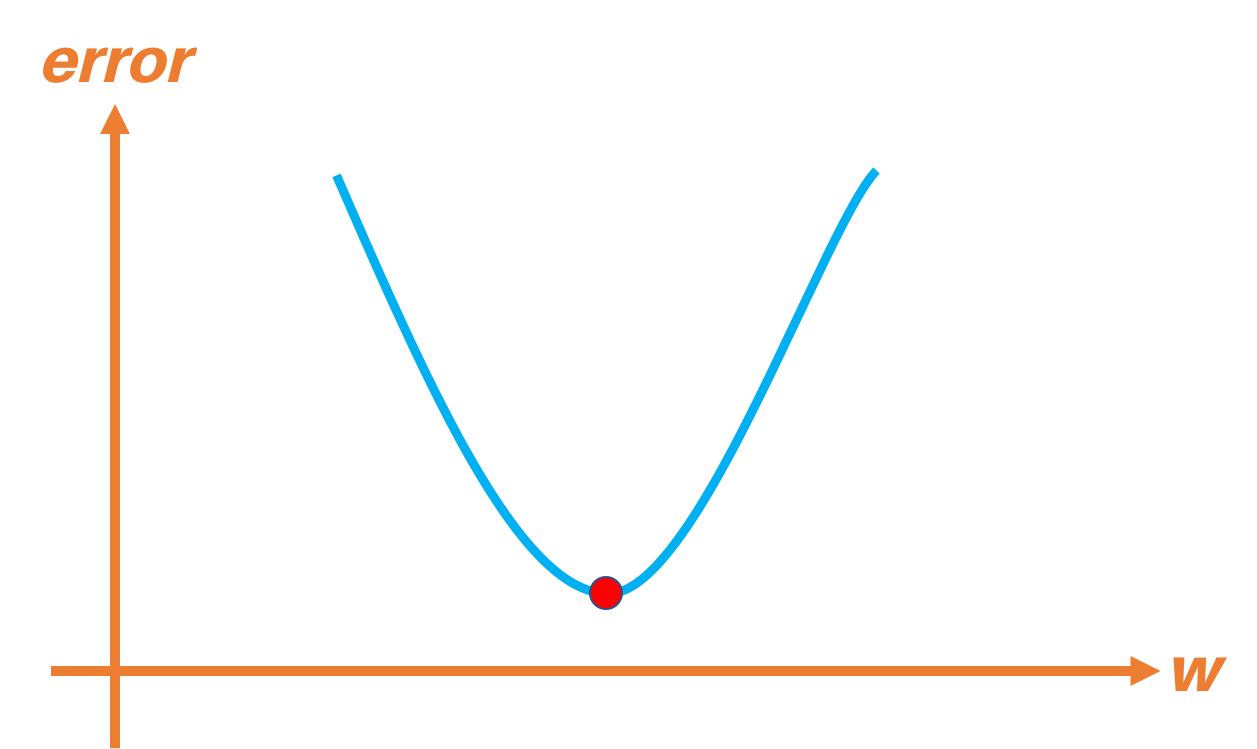
Características de la frontera de decisión
En la figura de abajo se muestra la evolución de la frontera de decisión a medida que avanza el proceso de entrenamiento. Es evidente que a medida que la pérdida se minimiza, la frontera de decisión permite mejorar progresivamente la clasificación de los datos:
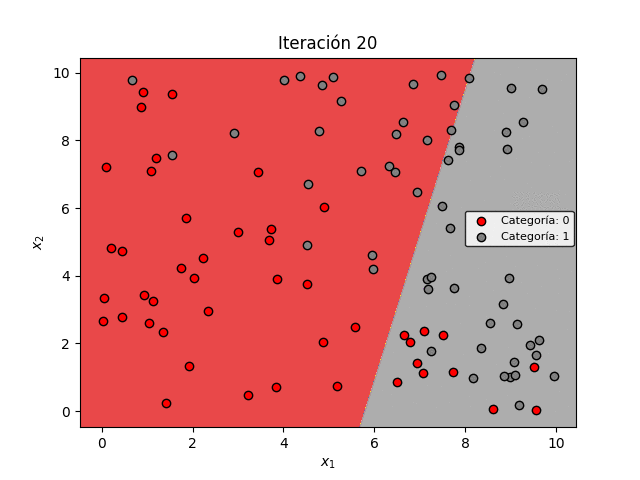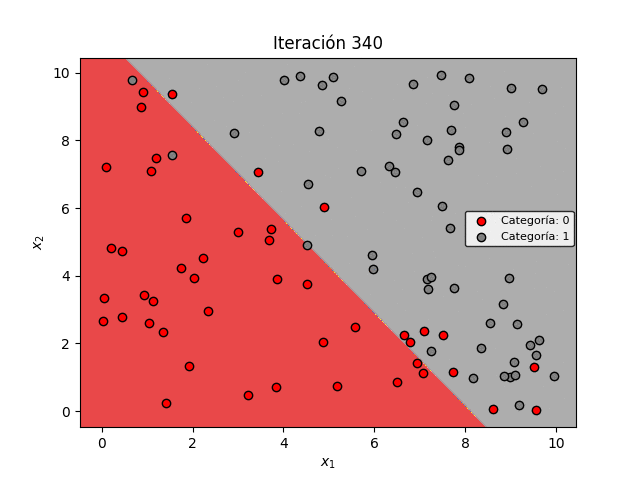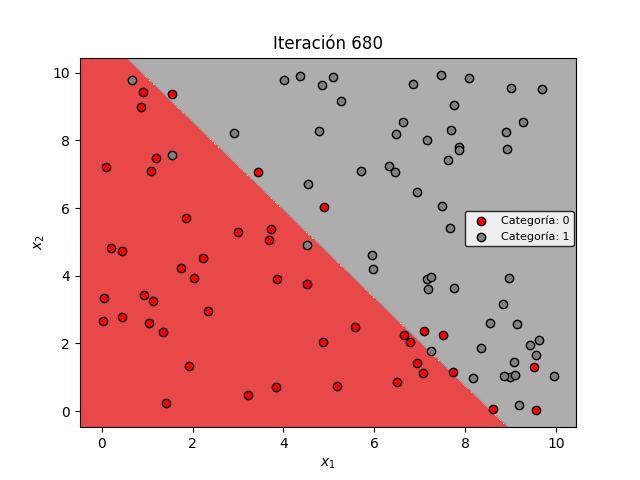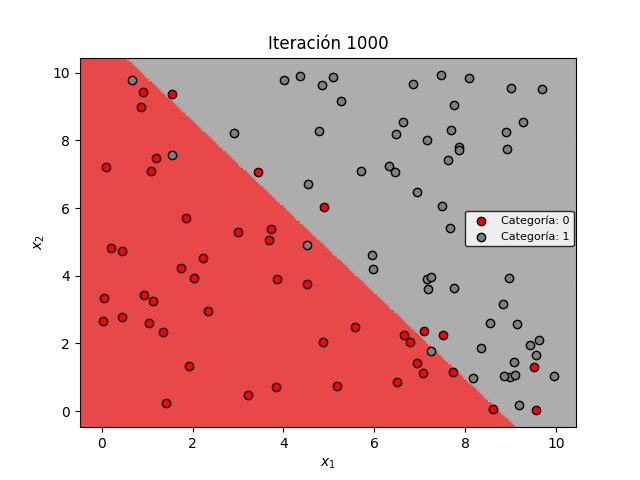
Sin embargo es importante observar una característica importante: la Regresión Logística siempre genera una frontera de decisión lineal. Es decir, la frontera siempre será una línea recta.
Lo anterior implica que si los datos tienen una distribución diferente y no pueden ser separados con una frontera lineal, entonces la Regresión Logística no resultará adecuada para la clasificación.
Más adelante veremos cómo las redes neuronales y los modelos Deep Learning permitirán ejecutar tareas de clasificación más complejas, en donde la frontera de decisión deja de ser lineal.
Conclusión
Hemos visto en detalle dos elementos fundamentales del Deep Learning: la Neurona Artificial y la Regresión Logística. Estos son los elementos más importantes a tener en cuenta:
- La Regresión Logística es un algoritmo que permite clasificar una serie de datos de entrada en una de dos posibles categorías. También recibe el nombre de regresión binaria.
- El algoritmo involucra dos pasos: la transformación de los datos de entrada y el uso de una función de activación.
- La transformación de los datos de entrada requiere el cálculo de los parámetros del modelo ($\vec{w}$ y $b$), el cual se hace de manera automática a través del entrenamiento.
- En el caso de la Regresión Logística, la función de activación usada se conoce con el nombre de función sigmoidal.
- La Neurona Artificial es una unidad algorítmica que se encarga precisamente de llevar a cabo la transformación de los datos y de aplicar una función de activación al resultado obtenido.
- El entrenamiento es simplemente un proceso de optimización que permite minimizar la función de pérdida. Con ello se logran aprender los parámetros del modelo.
- En la Regresión Logística, la función de pérdida se conoce como entropía cruzada.
- Una limitación de la Regresión Logística es que sólo permite clasificar datos que sean linealmente separables. Es decir que la frontera de decisión obtenida siempre será una línea recta.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: