Tutorial: Regresión Logística en Python y Keras

Agosto 13, 2018 por Miguel Sotaquirá

En este tutorial veremos cómo resolver un problema de clasificación binaria usando una Neurona Artificial (o Perceptrón) y el algoritmo de Regresión Logística en Keras.

Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.

¡Así que listo, comencemos!

Tabla de contenido

Video

Como siempre, en el canal de YouTube se encuentra el video de este post:

El algoritmo de Regresión Logística y Keras

Este algoritmo permite entrenar una Neurona Artificial (o perceptrón) para clasificar de forma automática un set de datos en una de dos posibles categorías (lo que se conoce comoclasificación binaria). Si quieres entender en qúe consiste este algoritmo, te sugiero revisar el artículo en donde explico la La Neurona Artificial y la Regresión Logística en detalle.

También te sugiero revisar el completo tutorial de Keras si deseas entender más detalles de esta librería.

El set de datos y definición del problema

Este set de datos fue tomado de una muestra de 100 estudiantes universitarios. Por cada estudiante se analizó el éxito o fracaso al presentar un examen, dado el número de horas de estudio y el número de horas de sueño.

Así, las variables de interés para este ejemplo serán:

Entrada x, que contendrá dos características: el número de horas de estudio ($x_1$) y el número de horas de sueño ($x_2$).
Salida y, correspondiente al resultado del examen: “1” para aprobado y “0” para no aprobado.

El objetivo de este ejercicio es implementar un modelo de Regresión Logística en Keras que permita clasificar los datos automáticamente en una de estas dos categorías.

Veamos inicialmente las librerías requeridas para esta implementación.

Librerías requeridas

La lectura del set datos se realizará usando la librería Pandas. El almacenamiento de datos en memoria y la visualización de los resultados requieren el uso de Numpy y Matplotlib respectivamente.

Estas son las líneas de código necesarias para la importación de estas librerías:

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

También es necesario importar los siguientes módulos de Keras:

Sequential: para crear el contenedor del modelo.
Dense: para especificar que el modelo realizará una Regresión Logística sobre los datos.
SGD: para usar la entropía cruzada como función de error y el Gradiente Descendente como método de optimización.

Éstas son las líneas de código correspondientes:

from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD

A continuación veremos cómo leer y visualizar los datos.

Lectura y visualización de los datos

En primer lugar realizamos la lectura de los 100 datos y los almacenamos en un DataFrame de Pandas:

datos = pd.read_csv('dataset.csv', sep=",")

A continuación creamos las variables de entrada y de salida. X (entrada) contendrá dos columnas (correspondientes a las características $x_1$ y $x_2$) y Y (salida) contiene la categoría a la que pertenece cada uno de los datos (“0” o “1”):

X = datos.values[:,0:2]
Y = datos.values[:,2]

Para visualizar los datos primero identificamos los índices correspondientes a la categoría “0” y aquellos correspondiente a la categoría “1”:

idx0 = np.where(Y==0)
idx1 = np.where(Y==1)

La visualización de los datos se logra usando la función scatter de Matplotlib, y asignando un color diferente a cada índice encontrado anteriormente:

plt.scatter(X[idx0,0],X[idx0,1],color='red',label='Categoría: 0')
plt.scatter(X[idx1,0],X[idx1,1],color='gray',label='Categoría: 1')
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.legend(bbox_to_anchor=(0.765,0.6),fontsize=8,edgecolor='black')
plt.show()

obteniendo el siguiente resultado:

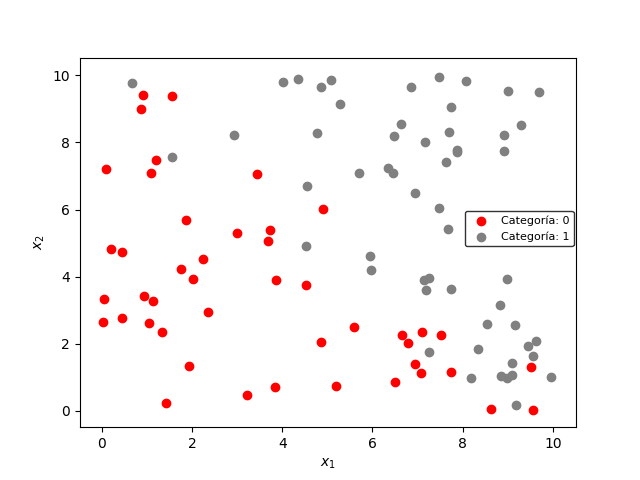
Set de 100 datos. Cada dato contiene dos características (x1, x2) y pertenece a una de dos posibles categorías (0: rojo, 1:gris)

Estos datos están agrupados en dos categorías, donde la frontera de decisión es una línea diagonal como la mostrada a continuación:

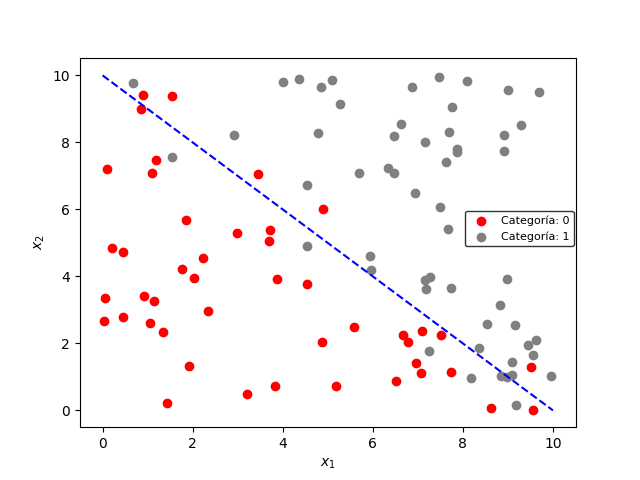
Frontera de decisión ideal que permite la clasificación de los datos

El objetivo esta Regresión Logística es precisamente encontrar de forma automática esta frontera de decisión.

Veamos entonces el código necesario para implementar el modelo en Keras.

Creación del modelo de Regresión Logística en Keras

Primero debemos hacer uso del módulo Sequential, seguido de los métodos add y Dense para añadir elementos al modelo.

El dato de entrada contiene dos dimensiones ($x_1$ y $x_2$), mientras que el dato de salida tendrá una dimensión (“0” ó “1”). Además, es necesario el uso de np.random.seed para garantizar la reproducibilidad de los resultados en diferentes computadores:

np.random.seed(1)
input_dim = X.shape[1]  # Dimensión: 2
output_dim = 1          # Dimensión: 1

Una vez definidas estas variables, podemos crear nuestro clasificador binario en Keras:

modelo = Sequential()
modelo.add(Dense(output_dim, input_dim = input_dim, activation='sigmoid'))

En la última línea de código hemos definido una función de activación sigmoidal (activation = 'sigmoid') que corresponde precisamente a la función usada en la Regresión Logística.

A continuación, hacemos uso del módulo SGD en conjunto con el método compile para definir el optimizador (Gradiente Descendente) y la pérdida a usar (entropía cruzada):

sgd = SGD(lr=0.2)
modelo.compile(loss='binary_crossentropy', optimizer=sgd, metrics=['accuracy'])

Para el optimizador hemos definido una tasa de aprendizaje (lr) igual a 0.2. Adicionalmente, además de la entropía cruzada (loss='binary_crossentropy') usaremos la precisión (metrics=['accuracy']) para medir el desempeño del modelo. Esta precisión es simplemente la cantidad de datos clasificador erróneamente, dividida entre la cantidad total de datos.

Una vez definido el modelo podemos llevar a cabo el proceso de entrenamiento para aprender los parámetros.

Entrenamiento del modelo

Al imprimir la información sobre el modelo (usando modelo.summary()):

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense_1 (Dense)              (None, 1)                 3
=================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
_________________________________________________________________

podemos observar que el modelo tiene tres parámetros entrenables (Trainable params: 3). Estos parámetros corresponden a los dos coeficientes w y al parámetro b.

En este caso usaremos un total de 1000 iteraciones y un batch_size igual a la cantidad total de datos (100):

num_epochs = 1000
batch_size = X.shape[0]

Finalmente, realizamos el entrenamiento usando el método fit, almacenando los resultados de cada iteración en una variable (historia) para poder graficarlos posteriormente:

historia = modelo.fit(X, Y, epochs=num_epochs, batch_size=batch_size, verbose=2)

Al ejecutar la anterior línea de código observamos que la precisión se incrementa progresivamente, iniciando con un valor cercano al 55% (acc = 0.55) en la iteración 1, hasta un valor del 89% (acc = 0.89) en la última iteración.

Veamos a continuación en detalle el comportamiento del modelo obtenido.

Resultados de la Regresión Logística

Proceso de entrenamiento

Veamos cómo se comportan la pérdida (loss) y la precisión del modelo (acc) a medida que avanzan las iteraciones. Para ello usamos estas líneas de código:

plt.subplot(1,2,1)
plt.plot(historia.history['loss'])
plt.ylabel('Pérdida')
plt.xlabel('Epoch')
plt.title('Comportamiento de la pérdida')

plt.subplot(1,2,2)
plt.plot(historia.history['acc'])
plt.ylabel('Precisión')
plt.xlabel('Epoch')
plt.title('Comportamiento de la precisión')
plt.show()

obteniendo el siguiente resultado:

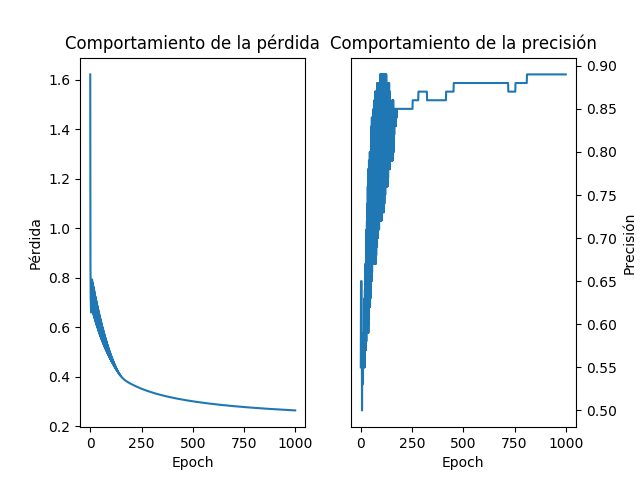
Comportamiento de la pérdida (izquierda) y la precisión del modelo (derecha) vs las iteraciones durante el entrenamiento

Observamos el comportamiento esperado: una disminución de la pérdida y un incremento de la precisión a medida que avanzan las iteraciones.

Dibujemos ahora la frontera de decisión generada por el modelo entrenado.

La frontera de decisión

Para visualizar el comportamiento del modelo frente a la clasificación de los datos, dibujaremos la frontera de decisión obtenida tras el proceso de entrenamiento.

Para ello implementamos la función dibujar_frontera:

def dibujar_frontera(X,Y,modelo,titulo):
    # Valor mínimo y máximo y rellenado con ceros
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01

    # Grilla de puntos
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # Predecir categorías para cada punto en la gruilla
    Z = modelo.predict_classes(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    fig = plt.figure()
    plt.contourf(xx, yy, Z, cmap=plt.cm.Set1, alpha=0.8)

    idx0 = np.where(Y==0)
    idx1 = np.where(Y==1)
    plt.scatter(X[idx0,0],X[idx0,1],color='red', edgecolor='k', label='Categoría: 0')
    plt.scatter(X[idx1,0],X[idx1,1],color='gray',edgecolor='k', label='Categoría: 1')
    plt.legend(bbox_to_anchor=(0.765,0.6),fontsize=8,edgecolor='black')

    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.title(titulo)

    plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    plt.show()

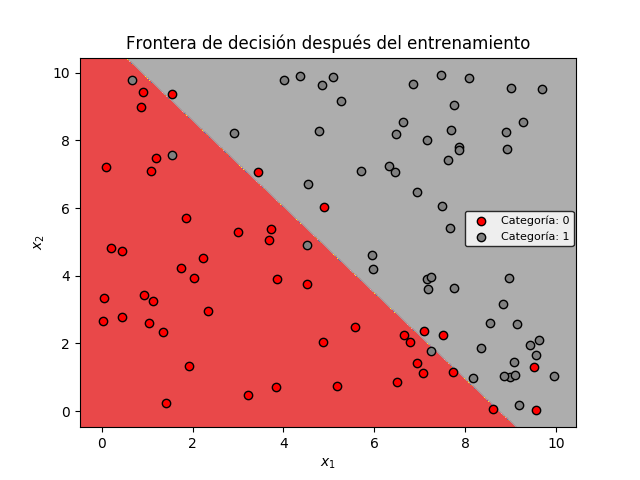
Frontera de decisión después del entrenamiento del modelo de Regresión Logística en Keras

Observamos que el modelo entrenado ha generado dos agrupaciones, correspondientes a cada categoría.

En la gráfica anterior, cuatro datos correspondientes a la categoría 1 (círculos grises) han sido clasificados incorrectamente (es decir, se encuentran en la región de color rojo, correspondiente a la categoría 0). De forma equivalente, siete datos de la categoría 0 (circulos rojos) han sido clasificados como pertenecientes a la categoría 1 (región de color gris).

Lo anterior quiere decir de los 100 datos, 11 fueron clasificados incorrectamente y 89 correctamente, lo que equivale a una precisión del 89%, que fue el valor obtenido en la última iteración del entrenamiento.

Incluso si se incrementa el número de iteraciones, la precisión no sobrepasará este 89%. Esto se debe a la forma como están distribuidos los datos, y a la limitación inherente de la Regresión Logística, que no permite obtener una frontera de decisión no lineal (la cual mejoraría la precisión en la clasificación).

Set de datos y código fuente

En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.

Conclusión

En este tutorial hemos visto cómo implementar el algoritmo de Regresión Logística en Keras. Estos son algunos aspectos importantes a tener en cuenta:

Los módulos Sequential y Dense de Keras permiten crear el modelo de Regresión Logística.
Dense permite definir la función de activación sigmoidal (activation='sigmoid') usada en esta Regresión Logística.
El módulo SGD permite usar el Gradiente Descendente como método de optimización. Al crear el objeto con este módulo se puede asociar la correspondiente tasa de aprendizaje que se usará durante el entrenamiento.
El método compile permite asociar el optimizador (Gradiente Descendente) y la función de error (binary_crossentropy, o entropía cruzada) al modelo creado inicialmente.
El entrenamiento se realiza con el método fit, que requiere, además de los datos de entrada y de salida, el número de iteraciones y el tamaño del lote (batch_size).
Tras el entrenamiento se obtiene una frontera de decisión lineal, por lo cual la precisión es de sólo el 89%.
Lo anterior se debe a que la Regresión Logística permite obtener únicamente fronteras de decisión lineales.

Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: