Regresión con Árboles de Decisión: el algoritmo CART
En este post veremos todos los detalles del algoritmo CART y de cómo usarlo para implementar Árboles de Decisión en una tarea de Regresión. Veremos en detalle cómo funciona paso a paso el algoritmo, cómo se construye el árbol de decisión, cómo se realiza la predicción con este árbol y cómo realizar la poda del mismo en caso de que sea necesario simplificarlo.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
Los árboles de decisión son uno de los algoritmos de aprendizaje supervisado más importantes del Machine Learning.
En el artículo anterior vimos como usar el algoritmo CART para implementar clasificadores con árboles de decisión. Pues en este artículo nos enfocaremos en la segunda parte de este algoritmo: la regresión.
Entenderemos cómo usar el algoritmo CART (por sus siglas en Inglés: Classification and Regression Trees) para construir el árbol de decisión de forma automática. De igual forma veremos cómo, una vez entrenado, se puede realizar la regresión para un dato nunca antes visto por el árbol. De igual forma hablaremos de la forma de controlar el crecimiento del árbol durante el entrenamiento (pre-poda) y una vez haya sido entrenado (post-poda).
Comencemos hablando de un tema esencial para entender cómo funcionan estos árboles: la Regresión.
¿Qué es la Regresión?
En una tarea de Regresión lo que buscamos es entrenar un modelo capaz de predecir el valor de una variable continua.
Por ejemplo, podríamos usar características como el área de un inmueble, el número de habitaciones y de baños y la antigüedad para predecir una variable continua que es el costo del inmueble:

Si hablamos de medicamentos podríamos usar como características la dosis en miligramos, el peso y la edad del paciente para intentar predecir la variable continua que es el porcentaje de efectividad del medicamento. La misma animación pero personalizada del caso anterior:
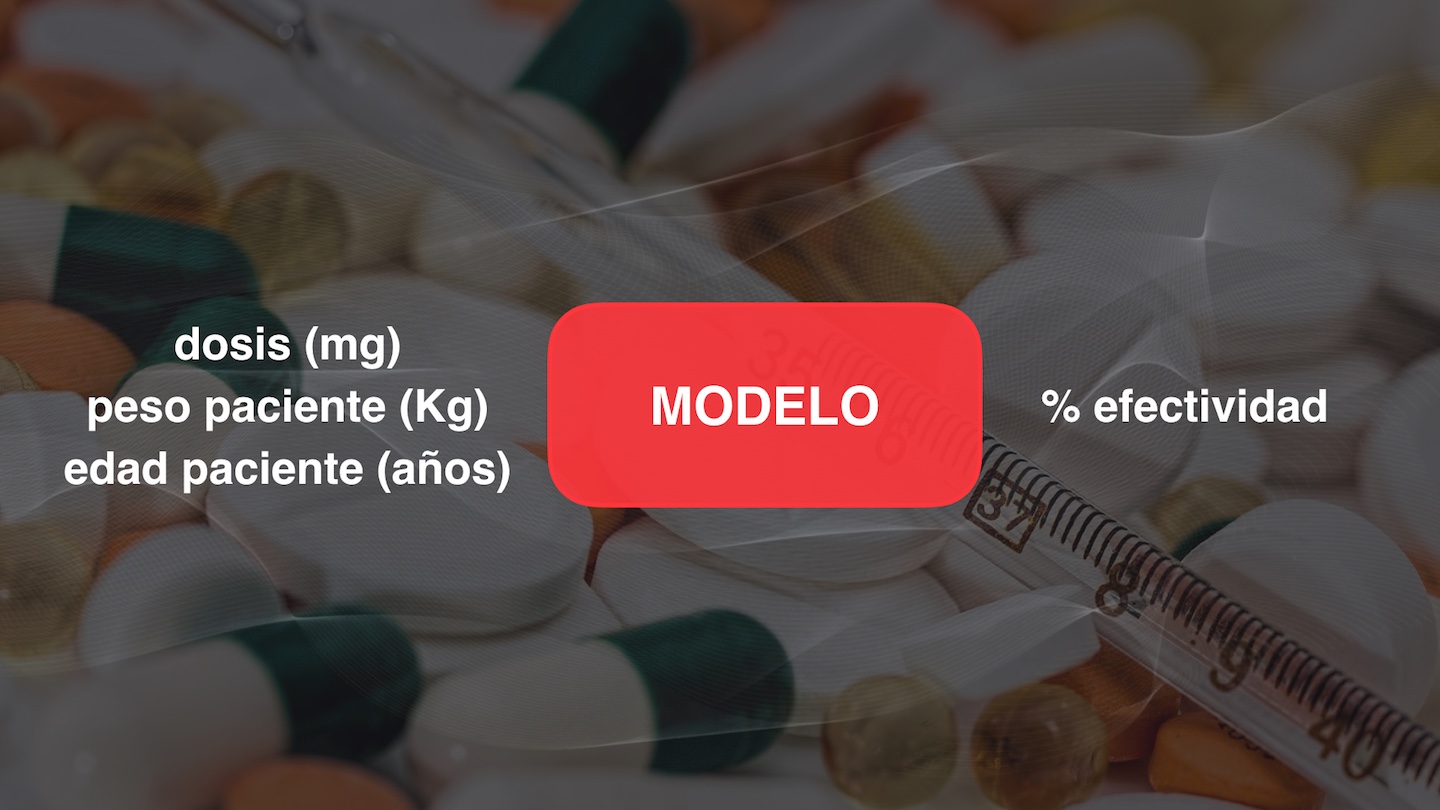
Para simplificar las cosas consideremos un problema de regresión con una sola característica. Con esto es suficiente para entender el principio básico de los árboles de regresión y del algoritmo CART. Una vez entendamos esto resultará muy fácil repetir cada paso del algoritmo para el caso en el cual tengamos dos o más características.
Volviendo al problema de los medicamentos, vamos a suponer que la única característica es la dosis en miligramos, y que la usamos para predecir el porcentaje de efectividad.
Si la relación entre estas dos variables es lineal, es decir, a mayor dosis mayor efectividad, el problema se puede resolver fácilmente usando el algoritmo de regresión lineal que vimos en un post anterior:
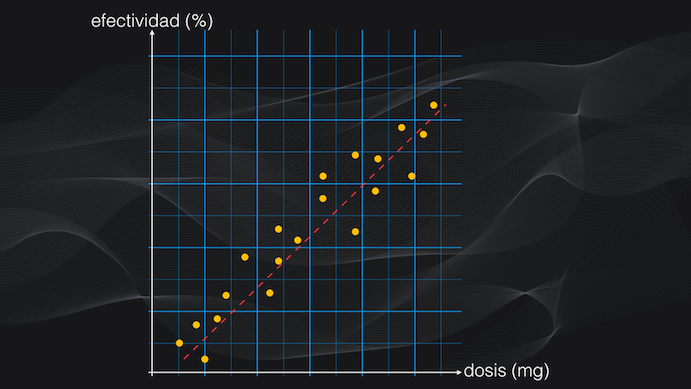
Pero compliquemos las cosas intencionalmente, porque en el mundo real es así: supongamos que la relación entre la efectividad y la dosis tiene el comportamiento que vemos en la figura: para un rango de dosis la efectividad es baja, para otro rango tiene un valor alto y para otro tiene un valor medio:
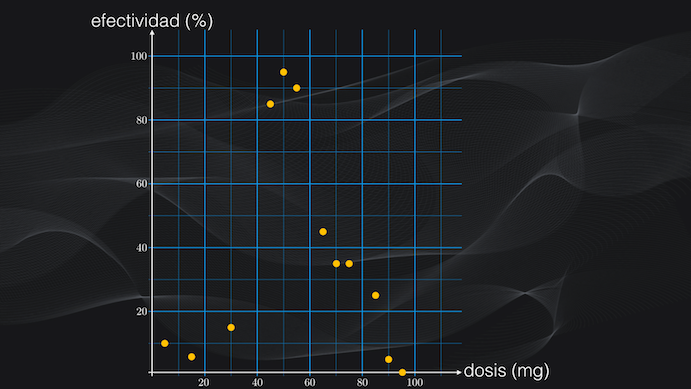
Acá necesitamos un modelo capaz de tener en cuenta estos diferentes rangos, y que logre predecir con precisión el porcentaje de efectividad para una dosis en particular. Y es aquí donde precisamente entran los árboles de decisión y el algoritmo CART.
Regresión con árboles de decisión: una idea general
En la regresión con árboles de decisión de manera iterativa se van realizando particiones binarias sobre el espacio de características (que en nuestro caso corresponde a la dosis en miligramos) buscando que en cada región obtenida cada vez se tengan distribuciones lo más homogéneas posible, es decir datos con niveles de efectividad del medicamento lo más cercanos entre sí.
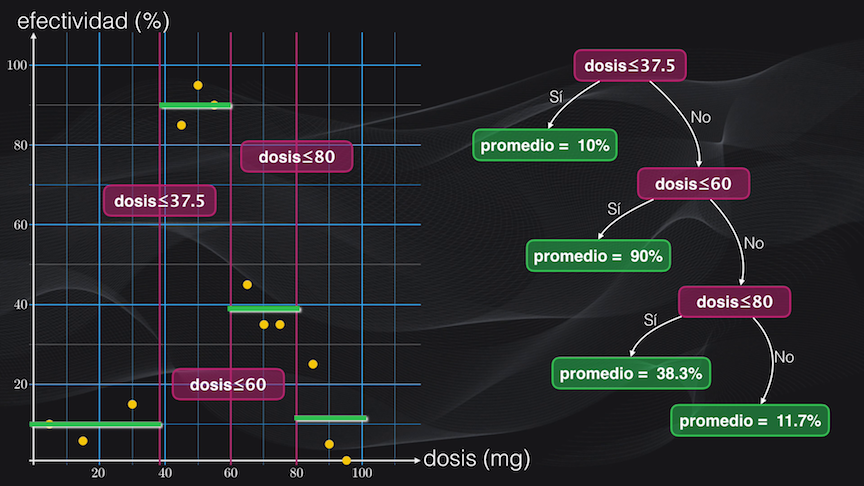
Veamos esto en detalle. Si establecemos por ejemplo una condición de una dosis menor o igual a 37.5 mg, los puntos a la izquierda no estarán muy dispersos y en promedio tendrán una efectividad del 10%, pero los del lado derecho, que no cumplen la condición, estarán más dispersos, y por tanto el promedio de la efectividad no será una representación muy precisa de esta región:
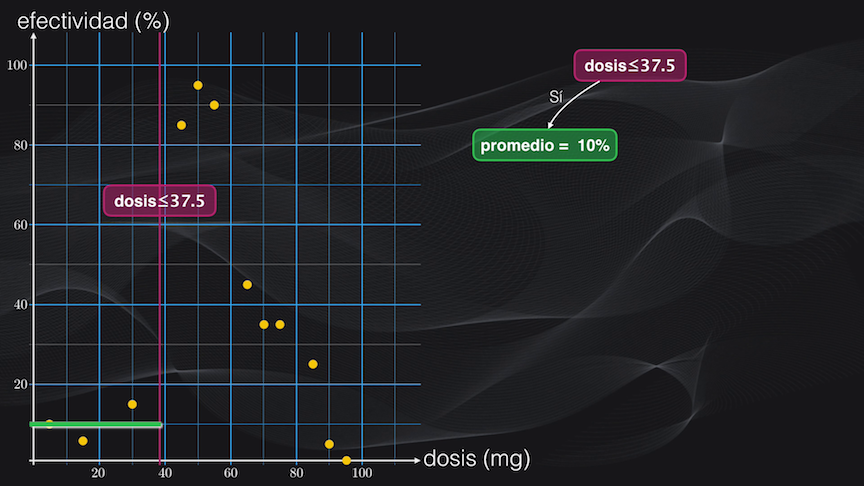
Así que dividimos esta región usando como criterio una dosis menor o igual a 60 miligramos. La partición resultante del lado izquierdo tiene baja dispersión y una efectividad promedio del 90%:
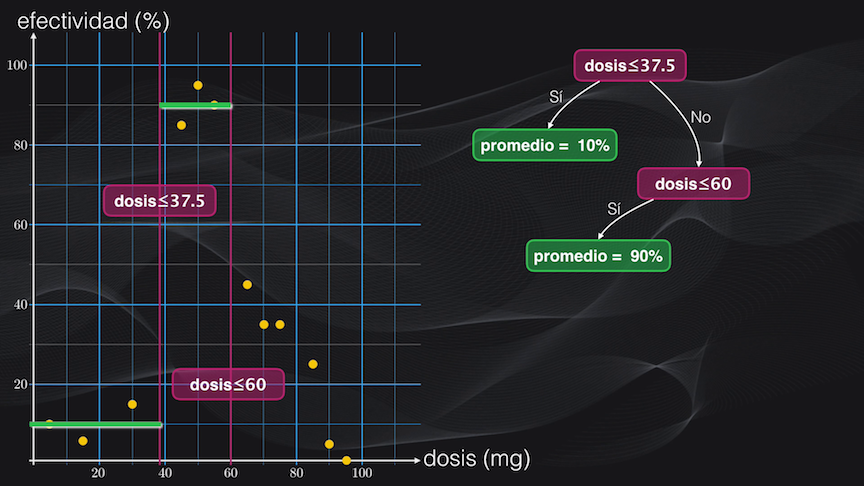
Pero la del lado derecho aún está muy dispersa, así que la dividimos nuevamente usando como condición una dosis menor o igual a 80 miligramos. Y acá resultan dos nuevas agrupaciones un poco más homogéneas: la de la izquierda con un promedio de 38.3% y la de la derecha con uno de 11.7%:
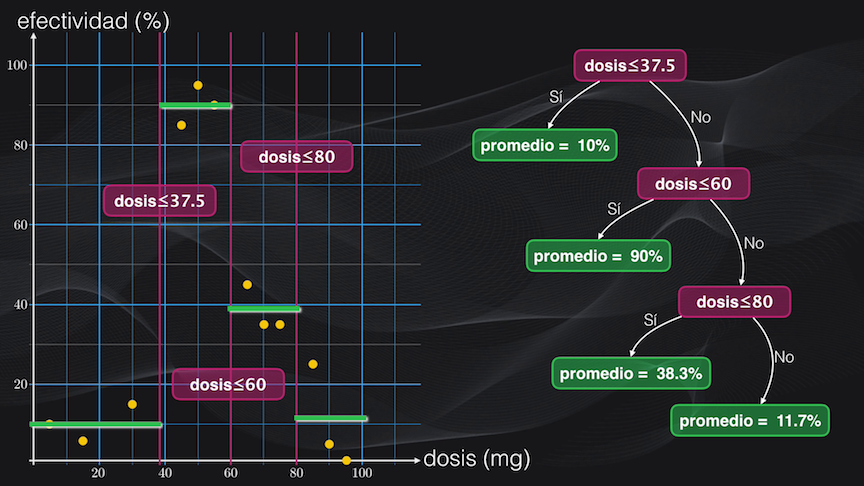
Y con este simple ejercicio acabamos de construir nuestro primer árbol de regresión. El nodo inicial (en violeta en la figura anterior, correspondiente a una dosis ≤ 37.5) se conoce como la raíz, los demás nodos (también en violeta) se conocen como nodos internos y las hojas (en color verde) son las terminaciones (es decir donde no hay más particiones). En este caso decimos que nuestro árbol tiene una profundidad igual a 3, que es la distancia máxima entre la raíz y la hoja más alejada, que en este caso corresponde a la hoja con promedio = 11.7%.
Bueno, ya tenemos una idea general de cómo se entrena un árbol de regresión. Pero todavía nos quedan varias preguntas por responder: ¿cómo lo usamos para realizar la regresión? o ¿cómo se construye de forma automática este árbol? o ¿cómo definimos en qué momento se dejan de hacer más particiones?
En el caso de la regresión, que en nuestro caso consiste en predecir el porcentaje de efectividad para un nuevo dato, basta con tomar la dosis correspondiente y recorrer el árbol entrenado, evaluando en cada nodo la condición establecida hasta llegar a una de las hojas. En este caso la predicción será simplemente el valor promedio de los datos que pertenecen a esta hoja, y que fue obtenido durante el entrenamiento:
El algoritmo CART en detalle
Ahora respondamos la segunda pregunta, es decir ¿cómo construir automáticamente este árbol de regresión?. Y acá precisamente entra en acción el algoritmo CART.
El primer paso es organizar ascendentemente los valores de la característica, y luego calcular el punto medio entre cada par de características consecutivas. A estos puntos los llamaremos “umbrales candidatos”.
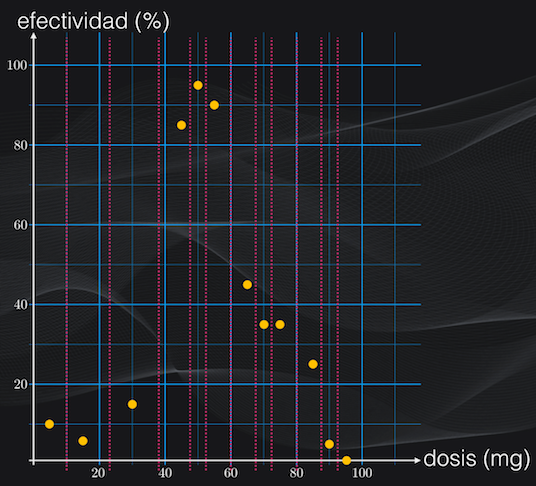
La idea ahora es seleccionar el mejor de estos “umbrales candidatos”, es decir el que genere las particiones con la menor dispersión posible de la variable continua (que en este caso es la efectividad).
Para entender cómo medir esta dispersión analicemos el primer umbral: una dosis menor o igual a 10 miligramos. Al usar esta condición la región izquierda tendrá un sólo punto y su dispersión será nula, porque su promedio será exactamente igual al valor de la efectividad, es decir del 10%:
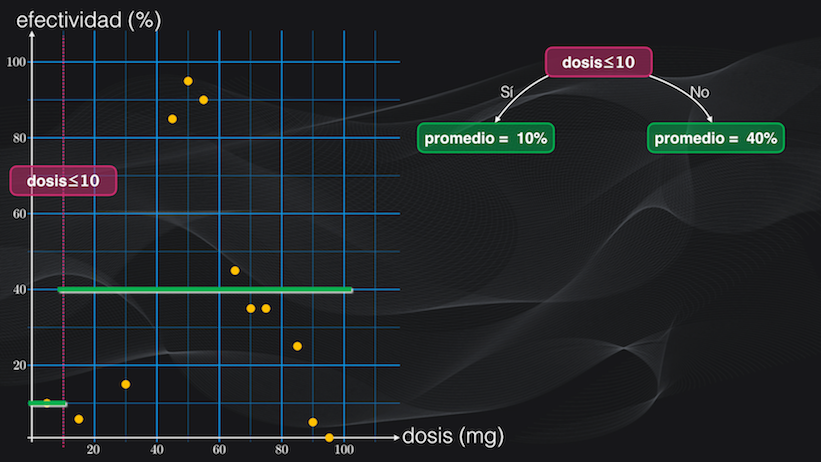
Pero la región derecha tiene un comportamiento diferente, pues tendrá 11 puntos con una efectividad promedio del 40%. Sin embargo, la mayoría de estos puntos se encuentra alejada del promedio, así que habrá una alta dispersión.
Para medir esta dispersión podemos simplemente promediar la diferencia existente entre el porcentaje de efectividad de cada punto y el valor de efectividad promedio de la región:
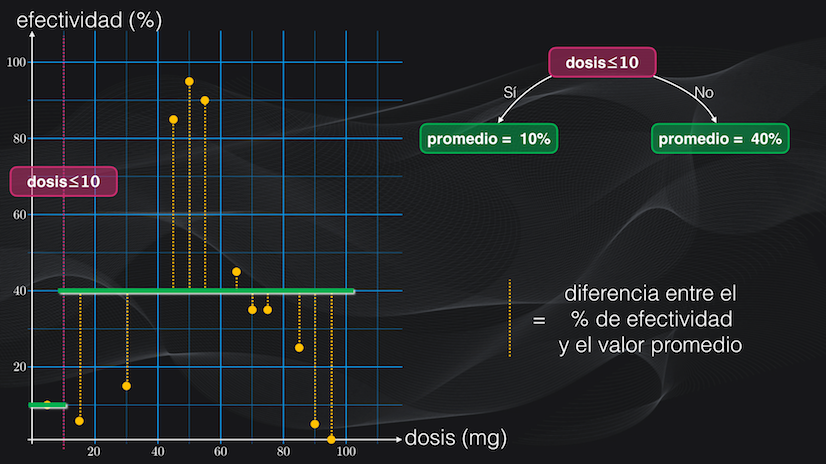
Pero para evitar que algunas diferencias positivas se anulen con diferencias negativas, elevaremos al cuadrado estas diferencias y luego sí las promediaremos. Y esta métrica que acabamos de definir se conoce como el error cuadrático medio:
$$ECM = \frac{1}{N} \sum_{i=1}^{N} (dato_i - promedio_{región})^2$$
donde $N$ representa el número total de datos de la región, $dato_i$ es el porcentaje de efectividad de cada uno de los datos que hace parte de esta región y $promedio_{región}$ es, ¡como su nombre lo indica!, el promedio de los porcentajes de efectividad de los $N$ datos que hacen parte de esta región.
Un error cuadrático medio igual a cero es la condición ideal, es decir una dispersión nula, mientras que entre más alto sea este error mayor será el grado de dispersión.
Si volvemos a las dos regiones que acabamos de obtener y calculamos su error cuadrático medio, veremos que la de la izquierda tiene un error igual a 0:
$$ECM_{izq} = \frac{(10-10)^2}{1} = 0$$
mientras que la de la derecha tiene una dispersión bastante alta, pues su error es mucho mayor: de 1127.3:
$$ECM_{der} = \frac{1}{11} \sum_{i=1}^{11} (dato_i - 40)^2$$ $$ECM_{der} = \frac{(5-40)^2 + (15-40)^2 + … + (0-40)^2}{11}=1127.3$$
Ahora, sabiendo el grado de dispersión de cada subregión, podemos calcular un puntaje para el umbral seleccionado, lo que llamaremos en adelante función de costo.
Para esto primero calculamos la dispersión promedio de cada subregión: tomamos su error cuadrático medio y lo multiplicamos por la fracción de datos que resulta en cada agrupación, con relación al número inicial de datos.
Así por ejemplo, la región izquierda tenía un error cuadrático medio igual a 0, y en total había 1 de los 12 datos iniciales, lo que equivale a una dispersión promedio igual a cero. En el lado derecho el error era igual a 1127.3 y se tenían 11 de los 12 datos iniciales, lo que equivale a una dispersión promedio igual a 1033.4.
Y con esta información calculamos la función de costo para este umbral, que será simplemente la suma de las dos dispersiones promedio que acabamos de obtener, es decir igual a 1033.4:
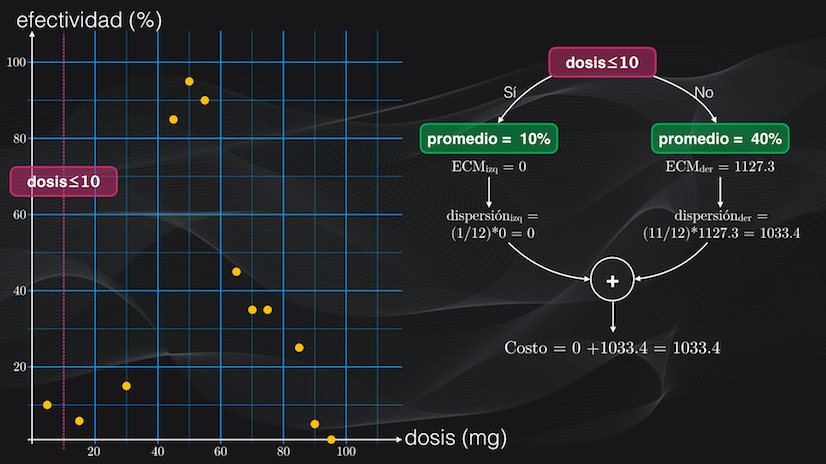
Perfecto, ya tenemos una métrica para evaluar qué tan buena o no es una partición. La idea es ahora repetir el mismo procedimiento del cálculo de la función de costo para cada umbral y una vez hecho esto tomar el umbral con la menor función de costo posible, que será precisamente el que genere las particiones con la menor dispersión. En este caso particular veremos que la mejor condición de todas es una dosis menor o igual a 37.5 miligramos:
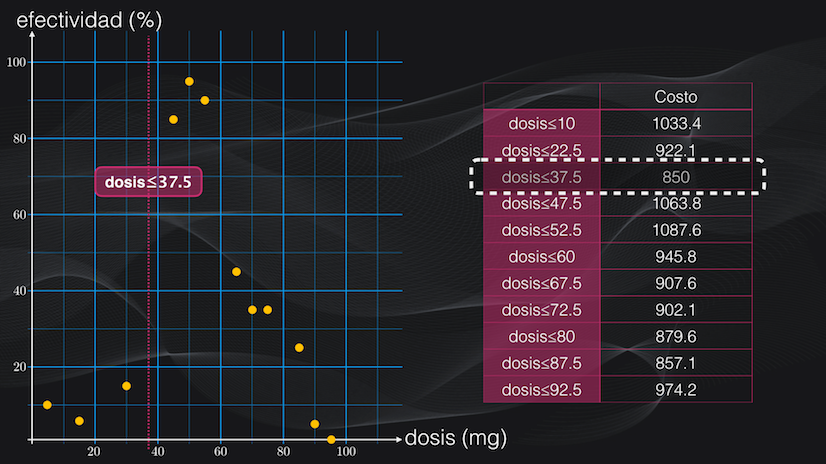
Y bien, ya hemos obtenido una primera partición. Ahora lo que podemos hacer es seguir refinando cada una de las regiones obtenidas, realizando precisamente más particiones.
Si por ejemplo nos enfocamos en la región del lado derecho (es decir a la derecha del umbral de 37.5 mg que acabamos de encontrar), vemos que aún se puede subdividir. Así que repetimos el algoritmo anterior: definimos los “umbrales candidatos” para esta región de interés y luego calculamos la función de costo de cada uno, y elegimos el umbral con el menor costo posible, que en este caso equivale a una dosis menor o igual a 60 mg:
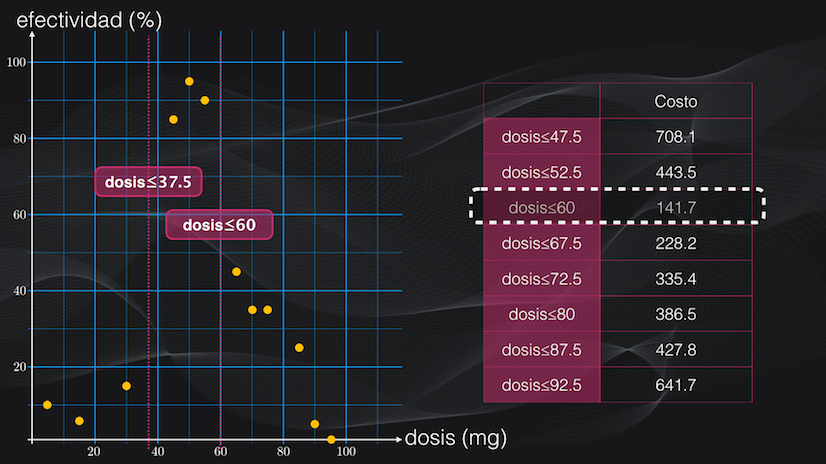
Y con esto ya tenemos la base del algoritmo CART para la regresión, que se puede resumir de la siguiente forma:
- Calcular los umbrales candidatos, que corresponden al punto intermedio entre dos valores consecutivos de las características
- Para cada umbral candidato obtener las dos particiones y calcular sus errores cuadráticos medios Calcular la función de costo de cada umbral candidato y elegir aquel con el menor costo
- Y repetir los pasos 1 a 3 de forma iterativa, hasta cumplir con un criterio de parada.
¿Cómo controlar el tamaño del árbol?: criterio de parada y poda
Pero nos quedaba una pregunta por responder, que era ¿cómo saber cuando debemos dejar de hacer más particiones? Pues la respuesta está precisamente en este término que acabamos de mencionar: el criterio de parada.
Si volvemos al árbol que acabamos de entrenar veremos que algunas de las hojas aún tienen algo de dispersión, así que podríamos seguir subdividiéndolas:
Pero si hacemos esto estaríamos obteniendo regiones más pequeñas, que se ajustarían prácticamente a un sólo dato, y al momento de intentar hacer la regresión el valor predicho no sería el adecuado.
Es decir que el árbol estaría haciendo overfitting: se ajustaría perfectamente al set de entrenamiento, pero no realizaría buenas predicciones con datos nunca antes vistos.
Para evitar que haya overfitting y que el árbol crezca de forma indiscriminada usamos precisamente un criterio de parada, que es simplemente una condición que establecemos para evitar que un nodo se siga subdividiendo.
El mínimo número de datos por hoja
El criterio de parada más usado es el mínimo número de datos por hoja. Por ejemplo en el árbol que acabamos de entrenar este criterio era igual a tres, lo cual quiere decir que no se realizarán más particiones a un nodo que alcance este mínimo número de datos.
Pero, si por ejemplo cambiamos este número a 2 tendremos un árbol con más hojas, mientras que si es igual a 4 el tamaño del árbol será más pequeño:
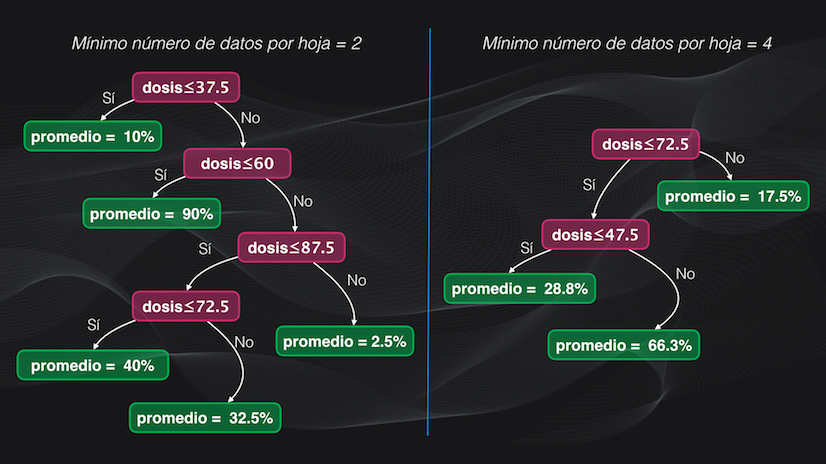
Este criterio de parada también se conoce como pre-poda.
Post-poda: poda de complejidad de costos
Pero también hay otra forma de controlar el tamaño del árbol, que consiste en primero entrenarlo y luego eliminar algunas hojas sobrantes, lo que se conoce como post-poda.
El algoritmo más usado para realizar este recorte es la poda de complejidad de costos, que funciona de la misma forma como lo vimos en el caso de la clasificación con árboles de decisión. La idea es que se usará un parámetro $\alpha$ (alpha) que controla el nivel de poda: con un $\alpha$ igual a 0 no se elimina ninguna hoja, y a medida que aumenta se eliminarán más hojas y se controlará por tanto el tamaño del árbol de regresión:
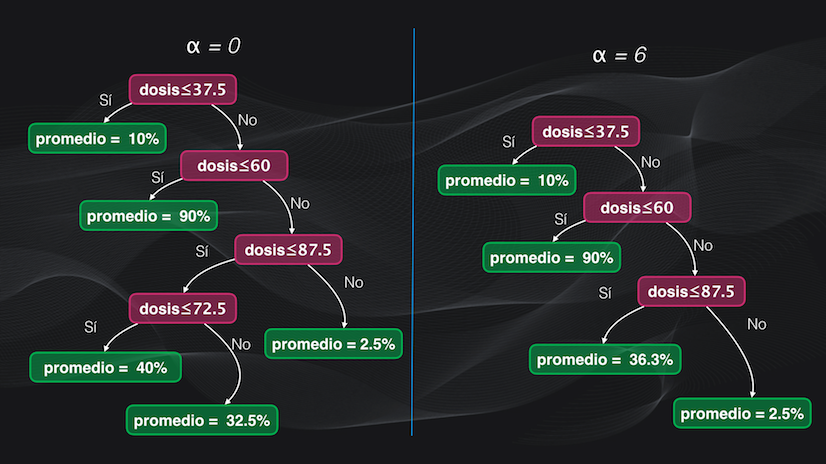
Conclusión
Bien, y con esto acabamos de ver detalladamente cómo funciona el algoritmo CART para entrenar y usar un árbol de decisión en una tarea de regresión.
El principio de funcionamiento es sencillo, pero más importante aún: el árbol resultante es fácil de interpretar, pues para entender cómo realiza la predicción basta con mirar en detalle cada condición en los diferentes nodos del árbol.
Y aunque para facilitar la explicación vimos el algoritmo para el caso de una sola característica (la dosis del medicamento en mg), exactamente el mismo procedimiento lo podemos aplicar iterativamente para dos o más características.
Si combinamos lo que acabamos de ver en este artículo con los árboles de clasificación que vimos anteriormente, tenemos dos de los métodos más poderosos del Machine Learning, que son la base de un algoritmo aún más poderoso que se conoce como los bosques aleatorios, que será el tema del próximo artículo.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario: