Tutorial: Regresión Multiclase con Python y Keras
En este tutorial veremos cómo implementar un clasificador multiclase usando Python y la librería Keras.
Para ello usaremos el set de datos “Iris”, que contiene 150 datos correspondientes a mediciones realizadas sobre la flor perteneciente a la especie Iris. Para cada uno de estos datos se realizaron las siguientes mediciones: longitud del sépalo, ancho del sépalo, longitud del pétalo y ancho del pétalo.
Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.
¡Así que listo, comencemos!
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
El set de datos
El set “Iris” fue creado en 1936 por el biólogo Ronald Fisher, y contiene 150 datos provenientes de tres variedades de flores de la especie Iris.
Los 150 datos de este set provienen de tres especies de flores: Iris setosa, Iris virginica e Iris versicolor.
Por su parte, cada uno de los datos está representado con cuatro características: longitud y ancho del pétalo, y longitud y ancho del sépalo. Para esta implementación usaremos sólo dos de estas características (la longitud y el ancho del sépalo).
El problema a resolver
Para clasificar el set de datos usaremos un modelo de Regresión Multiclase implementado en Keras.
Cada dato tendrá dos características de entrada (‘SepalLengthCm’, ‘SepalWidthCm’) y será clasificado en una de tres posibles categorías (‘Iris-setosa’, ‘Iris-versicolor’ o ‘Iris-virginica’).
En la figura de abajo se muestra la forma como están distribuidos los datos:
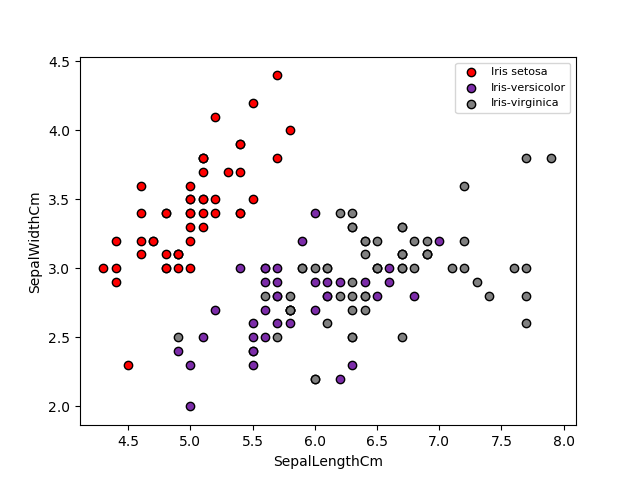
Como podemos ver, la categoría Iris setosa (en rojo) es fácilmente diferenciable. Por otra parte la frontera de decisión entre Iris versicolor (violeta) e Iris virginica (gris) no está claramente definida.
Veamos ahora cómo implementar y verificar el funcionamiento de este modelo de Regresión Multiclase en Keras.
Lectura y visualización del set de datos
La lectura de los datos (almacenados en formato .csv) la realizaremos usando la librería Pandas. En particular únicamente usaremos las columnas 1 (‘SepalLengthCm’), 2 (‘SepalWidthCm’) y 5 (‘Species’):
import pandas as pd
datos = pd.read_csv('Iris.csv',usecols=[1,2,5])
Los datos de entrada al modelo (X) así como la categoría a la que pertenece cada dato (Y) serán almacenados en arreglos de Numpy:
import numpy as np
X = datos.iloc[:,0:2].values
Y_str = datos.iloc[:,2].values
donde Y_str contiene el nombre de la categoría a la que pertenece cada dato.
Antes de graficar los resultados debemos representar estas categorías de forma numérica (Iris-setosa: categoría “0”; Iris-versicolor: categoría “1”; Iris-virginica: categoría “2”). Lo anterior se logra usando la función LabelEncoder de la librería scikit-learn:
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
encoder.fit(Y_str)
Y_num = encoder.transform(Y_str)
siendo Y_num el arreglo Numpy con la representación numérica de las categorías para cada uno de los 150 datos.
A continuación debemos realizar el pre-procesamiento de los datos para poderlos introducir al modelo implementado en Keras.
Representación one-hot de los datos
Y_num, el arreglo calculado anteriormente, contiene 150 etiquetas para cada uno de los datos de entrada.
Sin embargo, antes de realizar el entrenamiento del modelo, es necesario modificar la manera como están representadas estas categorías. En particular, cada una debe ser representada de una forma equivalente:
$$“0” \rightarrow (1,0,0)$$ $$“1” \rightarrow (0,1,0)$$ $$“2” \rightarrow (0,0,1)$$
La anterior representación recibe el nombre de one-hot, y permite calcular correctamente la función de pérdida usada en la Regresión Multiclase.
Para obtener esta representación se requiere el módulo np_utils de Keras:
from keras.utils import np_utils
n_clases = 3
Y = np_utils.to_categorical(Y_num,n_clases)
donde Y es el arreglo que contiene las categorías codificadas correctamente.
Una vez realizado el pre-procesamiento, podemos implementar el modelo en Keras.
Creación del modelo
En primer lugar definimos las dimensiones de cada dato de entrada y de la salida. Adicionalmente reiniciamos la semilla del generador aleatorio para la reproducibilidad del entrenamiento (np.random.seed):
np.random.seed(1)
input_dim = X.shape[1] # Dimensión de entrada: 2
output_dim = Y.shape[1] # Dimensión de salida: 3
A continuación, creamos el contenedor y agregamos elementos al modelo usando los módulos Sequence y Dense de Keras, así como el método add:
from keras.models import Sequential
from keras.layers import Dense
modelo = Sequential()
modelo.add(Dense(output_dim, input_dim=input_dim, activation='softmax'))
donde en la última línea hemos definido la función de activación softmax (activation = 'softmax') requerida por el algoritmo de Regresión Multiclase.
Por último, definamos el optimizador Gradiente Descendente y su tasa de aprendizaje (0.1). Adicionalmente, especificamos la función de error (entropía cruzada) y la métrica de desempeño (precisión):
from keras.optimizers import SGD
sgd = SGD(lr=0.1)
modelo.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
Una vez creado el modelo, podemos realizar el aprendizaje de los parámetros.
Entrenamiento
En esta etapa usaremos un total de 2000 iteraciones y un batch_size igual al número total de datos (150).
El modelo se entrena usando el método fit:
n_its = 2000
batch_size = X.shape[0]
historia = modelo.fit(X,Y,epochs=n_its,batch_size=batch_size,verbose=2)
Cuando ejecutamos el código veremos que la precisión del clasificador varía desde un 33% en la primera iteración hasta un 80% en la última.
Veamos en detalle cuáles son los resultados de este entrenamiento y el desempeño del modelo.
Resultados
En primer lugar analicemos el comportamiento de la pérdida y de la precisión del modelo a medida que avanzan las iteraciones:
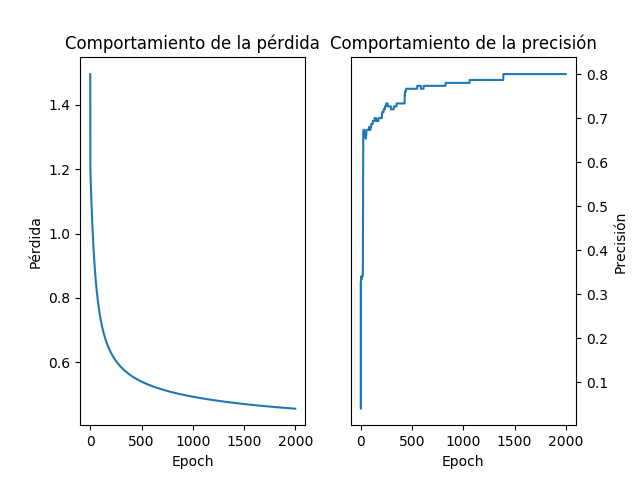
Se evidencia que hay una reducción del error y un aumento en la precisión del clasificador a medida que se incrementa el número de iteraciones.
Por otra parte, en la figura de abajo se muestran las fronteras de decisión obtenidas al final del entrenamiento:
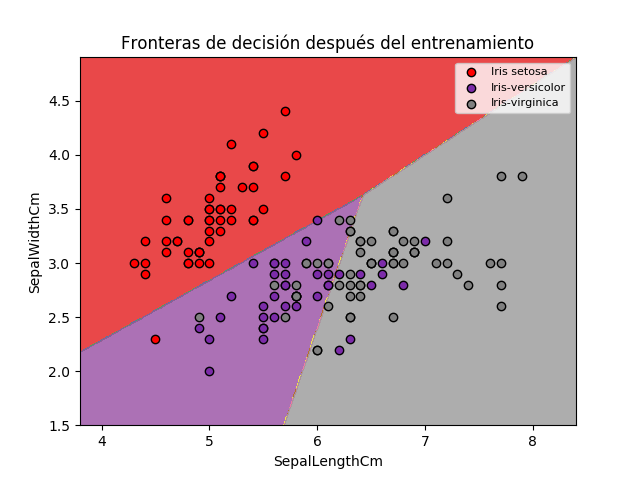
Podemos observar que los datos correspondientes a la categoría “0” son clasificados con una alta precisión. De hecho, tan solo hay un error, correspondiente al punto rojo ubicado en la región de color morado.
Finalmente, la clasificación de las categorías “1” y “2” tiene una menor precisión, debido a que estas no son linealmente separables. Lo anterior pone en evidencia una de las principales limitaciones de la Regresión Multiclase, que permite obtener únicamente fronteras de decisión lineales.
Conclusión
En este tutorial hemos visto un ejemplo de implementación del algoritmo de Regresión Multiclase en Keras. A continuación se resumen los aspectos más importantes a tener en cuenta:
- El módulo
LabelEncoderde la librería scikit-learn permite convertir las etiquetas de salida del formato string a una representación numérica. - Posteriormente, las etiquetas de salida obtenidas son transformadas al formato one-hot usando el módulo
np_utilsde Keras. - Los módulos
SequentialyDensepermiten crear el contenedor y los elementos característicos del modelo. - Finalmente, es importante observar que las fronteras de decisión son lineales, lo cual es una limitación del algoritmo de Regresión Multiclase. Es por este motivo que la precisión del clasificador no supera el 80%.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:
Set de datos y código fuente
En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.