Tutorial básico de Keras

Julio 30, 2018 por Miguel Sotaquirá

En este tutorial explico todos los elementos básicos para comenzar a implementar modelos de Deep Learning en Keras.

Keras es una de las librerías más usadas para la implementación de modelos Deep Learning. En este tutorial veremos cómo implementar el algoritmo de Regresión Lineal usando esta librería.

El objetivo de este tutorial es brindar a cualquier principiante las herramientas esenciales para posteriormente implementar modelos más complejos haciendo uso de esta librería.

Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.

Tabla de contenido

Video

Como siempre, en el canal de YouTube se encuentra el video de este post:

Introducción

En este tutorial veremos cómo implementar paso a paso un sencillo modelo de Regresión Lineal, y a través de este ejemplo entenderemos como usar Keras para crear y entrenar este modelo. Con estos conceptos básicos podremos más adelante implementar de forma muy similar modelos más complejos, como las Redes Neuronales, las Redes Convolucionales, las Redes Recurrentes y LSTM y las Redes Transformer.

Pero, antes de ver paso a paso esta implementación, analizaremos algunas de las principales librerías usadas en la actualidad para la implementación de modelos Deep Learning.

Alternativas existentes y ventajas de Keras sobre otras librerías

En la actualidad existen múltiples librerías, de acceso libre, que permiten el desarrollo de aplicaciones deep learning. Entre ellas las más importantes son TensorFlow (de Google), CNTK (de Microsoft) y Theano.

La principal desventaja de estas librerías es que requieren una curva de aprendizaje relativamente elevada, pues la cantidad de líneas de código requerida puede resultar considerable dependiendo de la complejidad del modelo.

Lo anterior hace que el tiempo de desarrollo para poner en funcionamiento un modelo sea relativamente alto. Es acá donde Keras se convierte en una ventaja.

¿Qué es Keras?

Keras es una librería que funciona como una interfaz de alto nivel para Tensorflow, CNTK o Theano, y que al momento de programar reduce significativamente la cantidad de código requerida para implementar un modelo. Esto hace más rápido el proceso de desarrollo de diferentes modelos Deep Learning.

Lo anterior quiere decir que al momento de programar usaremos la sintaxis definida por Keras, pero al momento de ejecutar el código Keras se encarga de hacer la traducción a la sintaxis usada por Tensorflow, CNTK o Theano.

Así, para poder usar Keras debemos previamente haber instalado cualquiera de los backends mencionados anteriormente (Tensorflow, CNTK o Theano).

Veamos ahora sí en detalle cómo usar Keras para implementar un modelo de Regresión Lineal.

El problema

En este tutorial usaremos el mismo set de datos usado en el ejemplo de regresión lineal implementado en Python. Estos datos fueron obtenidos a partir de 29 sujetos, de diferentes edades, y de los cuales se conoce el dato de la presión sanguínea durante la sístole.

En la figura de abajo se puede observar el comportamiento de la variable dependiente y (la presión sanguínea) a medida que cambia la variable independiente x (la edad):

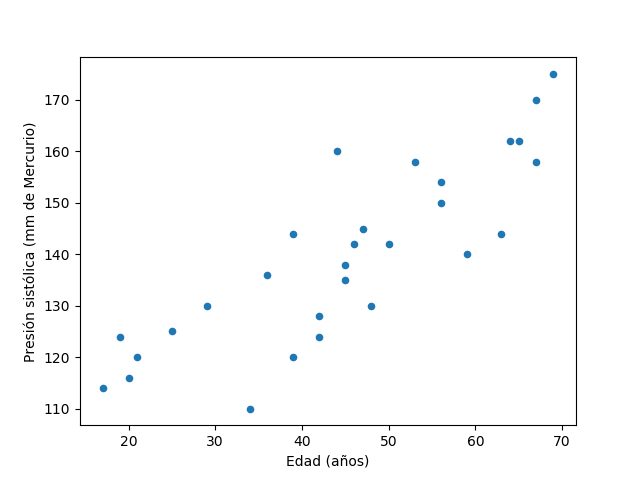
Relación lineal entre la edad (x) y la presión sanguínea (y)

El objetivo es entonces implementar un modelo de Regresión Lineal en Keras, para encontrar la línea recta que mejor se ajuste a los datos mostrados en la figura anterior. Esto equivale a encontrar los parámetros w (pendiente) y b (corte con el eje y).

Librerías requeridas

Usaremos la librería Pandas para la lectura del set de datos, y las librerías Numpy y Matplotlib para el almacenamiento de las variables en memoria y para graficar los resultados. Estas librerías se pueden importar con estas líneas de código:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Desde luego, también haremos uso de Keras, pero en particular debemos importar sólo unos cuantos módulos: Sequential, Dense y SGD. Estas son las líneas de código correspondientes:

from keras.models import Sequential
from keras.layers.core import Dense
from keras.optimizers import SGD

Más adelante veremos en detalle la función que cumple cada uno de estos módulos y la forma como se usan en la implementación de nuestro modelo.

Por ahora, hagamos la lectura de los datos.

Lectura de los datos

Estos serán almacenados en un DataFrame de Pandas, y posteriormente creamos las variables x y y para almacenar la edad y la presión sanguínea, respectivamente:

datos = pd.read_csv('dataset.csv', sep=",", skiprows=32, usecols=[2,3])
x = datos['Age'].values
y = datos['Systolic blood pressure'].values

Veamos ahora cómo implementar el modelo de Regresión Lineal en Keras.

Implementación del modelo en Keras

Uso de `Sequential()`

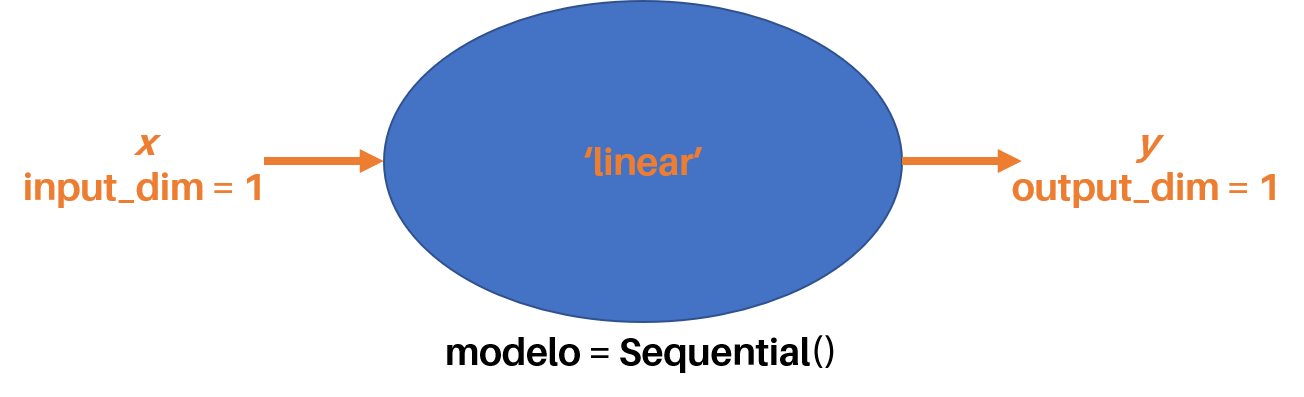
Este es el primer módulo que se usa en la implementación de un modelo en Keras. Sequential() permite crear un contenedor (una “caja vacía”) similar al mostrado en la figura de abajo, al que posteriormente podremos ir añadiendo otros elementos que definirán las características de nuestro modelo:

El módulo Sequential() de Keras crea un contenedor al cual se podrán agregar diferentes elementos que definan el modelo a implementar

Dicho contenedor se crea con la siguiente línea de código:

np.random.seed(2)
modelo = Sequential()

donde np.random.seed(2) permite replicar los resultados de esta implementación en diferentes computadores, al garantizar que todos los parámetros del modelo se inicializan de forma aleatoria pero siempre con los mismos valores.

A continuación añadiremos diferentes elementos a este modelo.

Uso de `Dense()`

Hasta el momento el modelo es simplemente un contenedor, que bien podría ser un modelo de Regresión Lineal o de Regresión Logística, una Red Neuronal o una Red Convolucional.

Para definir cuál será el contenido de este modelo debemos usar el módulo Dense. En particular este módulo requiere al menos tres parámetros de entrada:

output_dim: especifica el tamaño de los datos de salida. En este caso la salida será el valor correspondiente a la presión sanguínea, y por tanto la dimensión será igual a 1 (por ser simplemente un dato numérico, y no un vector o una matriz o una imagen).
input_dim: se refiere al tamaño de los datos de entrada. En este ejemplo el dato de entrada será la edad y, al igual que en el caso anterior, tendrá una dimensión igual a 1.
activation: permite definir la función de activación a utilizar, es decir si el modelo tendrá un comportamiento lineal o si lo usaremos para realizar, por ejemplo, una Regresión Logística o una Red Neuronal. En nuestro caso nos interesa implementar la Regresión Lineal, y por tanto usaremos la palabra clave linear.

Así, para definir un modelo que implemente la Regresión Lineal debemos usar el método add en conjunto con Dense para agregar los diferentes elementos al modelo. Esto se logra con las siguientes líneas de código:

input_dim = 1
output_dim = 1
modelo.add(Dense(output_dim, input_dim=input_dim, activation='linear'))

El anterior código equivale a “rellenar” el contenedor creado inicialmente con Sequential(), tal como se muestra en la figura de abajo:

Resultado de usar 'add' y 'Dense' para añadir elementos al modelo

Veamos ahora cómo definir el método que se usará para el entrenamiento del modelo.

Uso de `SGD()`

Hasta el momento se han definido los elementos del modelo (una entrada, una salida, activación lineal), pero aún no se ha especificado la forma como se calcularán los parámetros de la línea recta (w y b).

Para definir este procedimiento usamos el módulo SGD, cuyas siglas corresponden a Stochastic Gradient Descent, y que como su nombre lo indica permite especificar que el método de entrenamiento será precisamente el del Gradiente Descendente.

La siguiente línea de código permite crear una instancia de SGD con una tasa de aprendizaje (lr) igual a 0.0004:

sgd = SGD(lr=0.0004)

Una vez creado este objeto se debe enlazar con el modelo. Para ello se usa el método compile, en el cual se definirá adicionalmente la función de error (error cuadrático medio):

modelo.compile(loss='mse', optimizer=sgd)

donde loss='mse' se refiere precisamente al error cuadrático medio (mean squared error, mse) y optimizer=sgd permite especificar que el modelo hará uso del Gradiente Descendente para el entrenamiento.

Una vez creado el modelo, es posible visualizar de forma resumida sus características.

Uso de `summary()`

El método summary() permite imprimir en pantalla un resumen con las principales características del modelo:

modelo.summary()

Obteniendo el siguiente resultado:

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 1)                 2         
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________

¿Cómo interpretar esta información?

En este caso, summary indica que el modelo tiene una sola capa (dense_1) y que a la salida se tendrá una cantidad numérica (Output Shape: (None, 1)).

Otro elemento importante es el indicado en la columna Param #, que en este caso es igual a 2. Este valor corresponde a los dos parámetros (w y b) que hacen parte del modelo, dato que corresponde también al campo Trainable params: 2.

A continuación se realiza el entrenamiento del modelo para calcular de forma automática sus parámetros.

Entrenamiento del modelo

El entrenamiento se lleva a cabo con el método fit, el cual requiere al menos tres parámetros de entrada:

epochs: el número de iteraciones que se usarán durante el entrenamiento (en este caso serán 40,000).
batch_size: define la cantidad de datos que se usarán en cada iteración del entrenamiento. En este caso se tienen tan solo 29 datos, que será precisamente el mismo batch_size a usar. Cuando la cantidad de datos es elevada (miles o millones) es conveniente usar un batch_size pequeño (de unos cuántos miles de datos) para evitar problemas de almacenamiento en la memoria del computador.
verbose: permite imprimir en pantalla los resultados del entrenamiento en cada iteración. Puede tomar uno de tres valores: 0 para no imprimir resultados en pantalla, y 1 o 2 para imprimir en diferentes formatos. En este caso se usará un valor igual a 1.

Los resultados del entrenamiento se almacenarán en una variable (historia) que permitirá graficar posteriormente la pérdida vs las iteraciones.

El código correspondiente al entrenamiento es entonces el siguiente:

num_epochs = 40000
batch_size = x.shape[0]
historia = modelo.fit(x, y, epochs=num_epochs, batch_size=batch_size, verbose=1)

Resultados

Los parámetros w y b calculados tras el entrenamiento, se pueden imprimir en pantalla usando el siguiente código:

capas = modelo.layers[0]
w, b = capas[0].get_weights()
print('Parámetros: w = {:.1f}, b = {:.1f}'.format(w[0][0],b[0]))

obteniendo w=1.0 y b=93.5, que son valores idénticos a los obtenidos cuando se implementó la Regresión Lineal en Python.

La información almacenada en la variable historia permite graficar el comportamiento de la pérdida (error cuadrático medio, ECM) durante el entrenamiento. Adicionalmente es posible graficar el resultado de la regresión superpuesto a los datos originales:

plt.subplot(1,2,1)
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('ECM')
plt.title('ECM vs. epochs')

y_regr = modelo.predict(x)
plt.subplot(1, 2, 2)
plt.scatter(x,y)
plt.plot(x,y_regr,'r')
plt.title('Datos originales y regresión lineal')
plt.show()

con lo que se obtienen las siguientes gráficas:

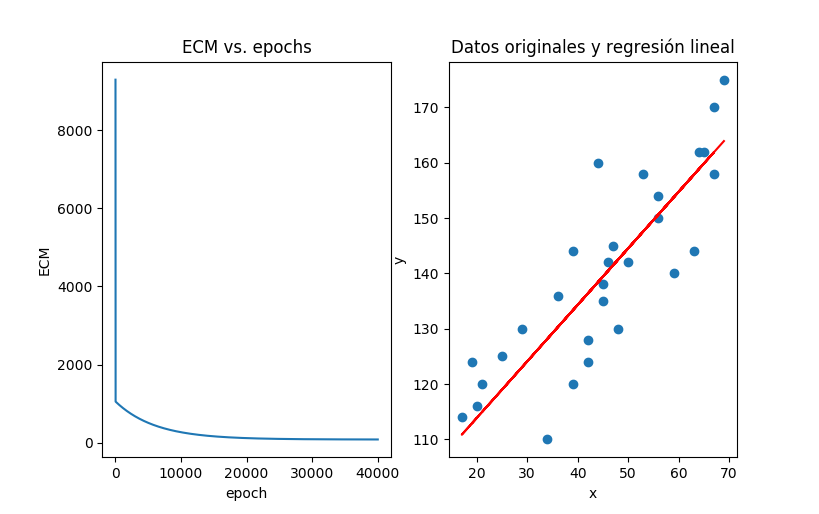
Izquierda: error cuadrático vs epochs. Derecha: resultado de la regresión lineal (línea roja) superpuesto a los datos originales (azul)

Se observa que a medida que avanzan las iteraciones el error cuadrático medio decrece, y que la recta resultante del entrenamiento se ajusta bastante bien a los datos originales.

Por último, veamos la forma de realizar una predicción con el modelo ya entrenado.

Predicción

Obtengamos el nivel de presión sanguínea para una persona de 90 años. Para ello usamos el método predict e introducimos la edad como un arreglo Numpy:

x_pred = np.array([90])
y_pred = modelo.predict(x_pred)
print("La presión sanguínea será de {:.1f} mm-Hg".format(y_pred[0][0]), " para una persona de {} años".format(x_pred[0]))

Conclusiones

Es evidente que la sintaxis de Keras y la forma de implementar un modelo usando esta librería es bastante intuitivo, y el código que se obtiene es compacto y fácil de interpretar.

Estos son algunos aspectos importantes a tener en cuenta:

Sin importar la complejidad del modelo, el primer módulo a utilizar es Sequential, que permite crear un contenedor al que poco a poco se irán agregando diferentes elementos dependiendo del modelo a implementar.
Posteriormente se usan el módulo Dense en conjunto con el método add para agregar entradas y salidas al modelo, así como la función de activación.
El módulo SGD es un optimizador en Keras, y permite hacer uso del método del gradiente descendente para el entrenamiento del modelo. La tasa de aprendizaje se puede definir usando la palabra clave lr(del Inglés learning rate)
Una vez creado el modelo y definido el optimizador, se puede hacer uso del método compile para enlazar dicho optimizador al modelo. En este también es posible definir la pérdida, a través de la palabra clave loss.
El entrenamiento del modelo se lleva a cabo usando el método fit, que requiere como parámetros de entrada el número de iteraciones (epochs) y el batch_size (la cantidad de datos de entrada que se usará en cada iteración del entrenamiento).
Finalmente, una vez entrenado el modelo, se puede calcular la predicción sobre un set de datos de entrada (x) diferente a los usados durante el entrenamiento. Para ello se usa el método predict.

El anterior procedimiento permite (con ligeras modificaciones) desarrollar modelos más complejos, como la Regresión Logística o Multiclase, o la implementación de Deep Neural Networks o de Redes Convolucionales.

Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:

Datos y código fuente

En este enlace de Github podrás descargar el set de datos y el código fuente de este tutorial.