Tutorial: clasificación de imágenes con Redes Neuronales en Python
En este post veremos cómo implementar una Red Neuronal en Python y Keras capaz de clasificar imágenes de dígitos, correspondientes al set MNIST.
Al final del artículo se encuentra el enlace para descargar el set de datos y el código fuente.
Tabla de contenido
Video
Como siempre, en el canal de YouTube se encuentra el video de este post:
Introducción
En un post anterir vimos qué es una Red Neuronal, que es una de las principales arquitecturas del Deep Learning y que permite, a través de la combinación de múltiples Neuronas Artificiales, extraer patrones de un set de datos que a simple vista no resultan aparentes para nosotros los humanos.
En este tutorial aprovecharemos esta utilidad de las Redes Neuronales para crear un clasificador de imágenes. El tutorial está dividido en cuatro partes: primero veremos cuál es el set de datos, luego hablaremos del pre-procesamiento de estos datos, luego implementaremos la Red Neuronal en Keras y finalmente analizaremos su desempeño.
Comencemos entonces con el set de datos.
El set de datos
El set que usaremos en este tutorial se llama MNIST, el cual contiene un total de 70,000 imágenes cada una de las cuales corresponde a una de 10 posibles categorías: los dígitos del 0 al 9.
La particularidad de este set de datos es que dichos dígitos han sido escritos por diferentes personas. El reto de la Red Neuronal que crearemos está en clasificar correctamente la mayor parte de estos dígitos independientemente de cómo hayan sido escritos.
En la figura de abajo vemos un ejemplo de diferentes dígitos que hacen parte de este set:

Para comenzar, realizaremos la lectura del set de datos. Esta lectura resulta sencilla teniendo en cuenta que Keras, la libreería que usaremos para implementar la Red Neuronal, ya contiene una función que fácilmente permite importar el set MNIST:
from keras.datasets import mnist
De igual forma, el módulo mnist permite separar de forma automática este set en entrenamiento (con 60,000 imágenes) y validación (con 10,000):
(x_train, y_train), (x_test, y_test) = mnist.load_data()
Cada elemento de estos sets contiene cada una de las imágenes (almacenadas en las variables x_train y x_test) y la categoría a la que pertenecen (almacenadas en las variables y_train y y_test).
Como cada imagen tiene un tamaño de 28x28 pixeles, las variables x_train y x_test serán por tanto arreglos de 60000x28x28 y 10000x28x28, mientras que y_train y y_test serán simplemente vectores de 60000 y 10000 elementos respectivamente.
Podemos visualizar algunas imágenes del set de entrenamiento usando las siguientes líneas de código:
import matplotlib.pyplot as plt
import numpy as np
ids_imgs = np.random.randint(0,x_train.shape[0],16)
for i in range(len(ids_imgs)):
img = x_train[ids_imgs[i],:,:]
plt.subplot(4,4,i+1)
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.title(y_train[ids_imgs[i]])
plt.suptitle('16 imágenes del set MNIST')
plt.show()

Pre-procesamiento del set de datos
Antes de introducir las imágenes a la Red Neuronal es necesario reajustarlas. Esto debido a que las Redes Neuronales sólo aceptas vectores como datos de entrada, pero cada imagen es una matriz de 28x28 elementos.
Así que cada una de estas matrices debe ser convertida a un vector, lo cual se logra fácilmente con la función reshape de Numpy:
X_train = np.reshape( x_train, (x_train.shape[0],x_train.shape[1]*x_train.shape[2]) )
X_test = np.reshape( x_test, (x_test.shape[0],x_test.shape[1]*x_test.shape[2]) )
Al usar esta función reshape estamos reajustando el tamaño del set de entrenamiento, pasando de un arreglo de 60000x28x28 a uno de 60000x784, lo cual quiere decir que cada una de las 60,000 imágenes de entrenamiento será ahora un vector de 28x28 = 784 elementos. Algo similar sucede con el set de validación, pasando de un arreglo de 10000x28x28 a uno de 10000x784.
Adicionalmente, para lograr la convergencia del algoritmo del Gradiente Descendente durante el entrenamiento de la Red Neuronal, debemos garantizar que la intensidad de cada pixel en las imágenes se encuentra en un rango de valores relativamente pequeño. Como cada pixel en el set de datos original tiene intensidades desde 0 (tonalidades oscuras) hasta 255 (tonalidades claras), esta normalización se logra simplemente dividiendo cada imagen entre 255:
X_train = X_train/255.0
X_test = X_test/255.0
Finalmente debemos reajustar la representación numérica de las categorías, que se encuentra en los arreglos y_train y y_test.
La idea es que cada categoría (del 0 al 9) será representada en el formato one-hot, es decir con un vector de 10 elementos (es decir el mismo número de categorías) donde sólo uno de estos elementos será diferente de cero (de allí el nombre one-hot).
Por ejemplo, si la categoría es $0$ la representación one-hot correspondiente será el arreglo $[1, 0, 0, 0, 0, 0, 0, 0, 0, 0]$, para la categoría $1$ la representación será el arreglo $[0, 1, 0, 0, 0, 0, 0, 0, 0, 0]$ y así sucesivamente.
Esta conversión al formato one-hot se puede implementar fácilmente usando la función np_utils de Keras:
from keras.utils import np_utils
nclasses = 10
Y_train = np_utils.to_categorical(y_train,nclasses)
Y_test = np_utils.to_categorical(y_test,nclasses)
Y bien, con esto ya estamos listos para implementar la Red Neuronal.
Creación y entrenamiento de la Red Neuronal en Keras
Implementación de la arquitectura básica
Nuestra Red Neuronal tendrá una capa de entrada con 784 nodos, es decir exactamente igual al tamaño de cada una de las imágenes aplanadas. Además tendrá una sola capa oculta con 15 neuronas y función de activación ReLU, así como una capa de salida con función de activación softmax y 10 neuronas de salida (correspondientes a las 10 diferentes categorías: del 0 al 9).
En primer lugar debemos fijar la semilla del generador aleatorio. Esto debido a que cuando creamos la Red Neuronal en Keras los parámetros de la misma son inicializados con valores aleatorios; para garantizar que siempre que ejecutemos el código lleguemos exactamente al mismo desempeño de la Red se hace necesario introducir la siguiente línea de código:
np.random.seed(1)
con lo que garantizaremos la reproducibilidad del entrenamiento.
Adicionalmente debemos definir el tamaño del dato de entrada (784 elementos) y del de salida (1 elemento):
input_dim = X_train.shape[1]
output_dim = Y_train.shape[1]
Ahora sí podemos crear la Red Neuronal con la ayuda de Keras. En primer lugar debemos crear un contenedor en donde almacenaremos nuestro modelo, para lo cual usamos el módulo Sequential:
from keras.models import Sequential
modelo = Sequential()
Luego usamos el módulo Dense para agregar, con ayuda de la función add y de manera secuencial, la capa de entrada, la capa oculta y la capa de salida:
from keras.layers import Dense
modelo.add( Dense(15, input_dim=input_dim, activation='relu'))
modelo.add( Dense(output_dim, activation='softmax'))
En el código anterior podemos ver que la capa de entrada y la capa oculta se crean en una misma línea de código (modelo.add( Dense(15, input_dim=input_dim, activation='relu'))). En particular, al usar Dense debemos especificar el número de neuronas de la capa oculta (15), así como el tamaño del dato de entrada (parámetro input_dim) y la función de activación (parámetro activation).
Por su parte, para la capa de salida (modelo.add( Dense(output_dim, activation='softmax'))) basta con especificar únicamente el tamaño del dato de salida (output_dim) así como la función de activación (parámetro activation).
Al usar modelo.summary() podemos imprimir en pantalla las características de nuestro modelo:
modelo.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 15) 11775
_________________________________________________________________
dense_1 (Dense) (None, 1) 16
=================================================================
Total params: 11,791
Trainable params: 11,791
Non-trainable params: 0
Aquí podemos ver que la Red Neuronal que acabamos de crear contiene un total de 11.791 parámetros a entrenar. Se trata de una Red relativamente sencilla, pues usualmente las redes usadas convencionalmente contienen cientos de miles o millones de parámetros.
Compilación de la Red Neuronal
Antes de entrenar el modelo debemos definir los parámetros que usaremos para el entrenamiento. Esto se conoce como compilar el modelo, y equivale a:
- Definir la función de error a utilizar, que por tratarse de una regresión multiclase corresponde a la entropía cruzada. En el post acerca de la Regresión Logística se describe en detalle esta función de error, que es la usada convencionalmente para el diseño de clasificadores. En Keras esta función se describe usando el parámetro
loss='categorical_crossentropy'. - Definir el método de optimización que permitirá minimizar la función de error definida anteriormente, pues recordemos que el entrenamiento es básicamente un proceso de optimización. En nuestro caso usaremos el algoritmo del Gradiente Descendente, que en Keras equivale al módulo
SGD. - Finalmente definimos la métrica de desempeño de la Red Neuronal, es decir la forma como determinaremos qué tan buena resulta la clasificación. En este caso usaremos la precisión, que es simplemente el número de aciertos en la clasificación sobre el número total de datos. En Keras esto se logra usando el parámetro
metrics=['accuracy'].
Los elementos descritos anteriormente se introducen a una única función (compile) que permite realizar la compilación del modelo.
El código completo es entonces:
from keras.optimizers import SGD
sgd = SGD(lr=0.2)
modelo.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
En donde hemos definido una tasa de aprendizaje de 0.2 (lr=0.2) para el algoritmo del Gradiente Descendente.
### Entrenamiento del modelo
Para entrenar la Red Neuronal usaremos 30 iteraciones:
num_epochs = 50
Además, teniendo en cuenta que el set de entrenamiento contiene 60.000 imágenes, para evitar problemas de almacenamiento en memoria durante el entrenamiento, optaremos por presentar al modelo lotes de tan sólo 1024 imágenes.
Esto quiere decir que Keras seleccionará aleatoriamente grupos de 1024 imágenes de entrenamiento, las presentará al modelo, realizará el entrenamiento, repetirá el proceso con otro lote de 1024 imágenes y así sucesivamente hasta que en cada iteración presente las 60.000 imágenes al modelo.
La definición de este tamaño de lote se realiza con el parámetro batch_size.
Con estos parámetros definidos podemos realizar el entrenamiento, para lo cual haremos uso de la función fit:
batch_size = 1024
historia = modelo.fit(X_train, Y_train, epochs=num_epochs, batch_size=batch_size, verbose=2)
El parámetro verbose=2 se usa simplemente para que se imprima en pantalla el resultado del entrenamiento durante cada iteración. Adicionalmente podemos observar que cada iteración del entrenamiento será almacenada en la variable historia, lo que nos permitirá obtener una gráfica del error y de la precisión del modelo durante cada iteración.
Una vez ejecutado el código anterior veremos que en la última iteración se alcanza una precisión bastante alta para este modelo, cercana al 95%:
Epoch 50/50
59/59 - 0s - loss: 0.1713 - accuracy: 0.9507
Veamos en detalle cómo se comporta el valor de la función de error durante cada iteración. Teniendo en cuenta que el entrenamiento es un proceso de optimización, es de esperar que a medida que avanza el entrenamiento el valor del error irá disminuyendo.
Para verificar esto usamos el siguiente código:
plt.subplot(1,2,1)
plt.plot(historia.history['loss'])
plt.title('Pérdida vs. iteraciones')
plt.ylabel('Pérdida')
plt.xlabel('Iteración')
Por otra parte, si obtenemos una gráfica de la precisión del modelo vs. el número de iteraciones, esperaríamos observar un comportamiento opuesto al del error: a medida que avanza el entrenamiento la precisión debería ser cada vez más alta. En este caso usamos el siguiente código:
plt.subplot(1,2,2)
plt.plot(historia.history['acc'])
plt.title('Precisión vs. iteraciones')
plt.ylabel('Precisión')
plt.xlabel('Iteración')
plt.show()
Al obtener las dos gráficas anteriores observamos el siguiente comportamiento:
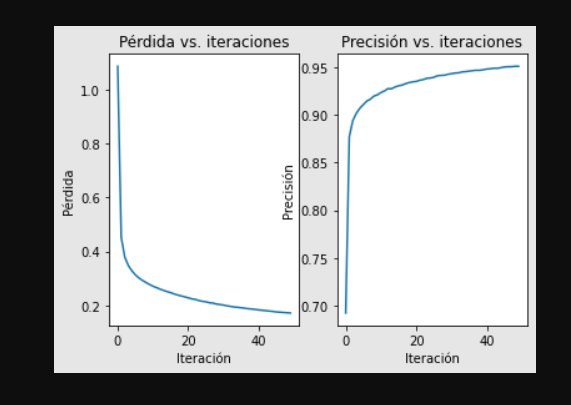
Analizando estas gráficas podemos constatar el comportamiento esperado: el error disminuye progresivamente mientras que la precisión aumenta a medida que avanzamos en el entrenamiento.
Validación del modelo
Hasta el momento parece que tenemos un modelo con un buen desempeño, pero debemos tener en cuenta que sólo hemos usado el set de entrenamiento.
Para validar el comportamiento de la Red Neuronal se hace necesario usar un set de datos que el modelo no haya visto previamente. Este set de datos es el set de validación (X_test, Y_test).
Para poner a prueba el modelo con este set de validación haremos uso en primer lugar de la función evaluate, que nos permite calcular la precisión del modelo con dicho set de datos:
puntaje = modelo.evaluate(X_test,Y_test,verbose=0)
print('Precisión en el set de validación: {:.1f}%'.format(100*puntaje[1]))
Al ejecutar el código anterior vemos que nuestro modelo alcanza una precisión del ¡94.4%!, un excelente resultado teniendo en cuenta que se trata de una simple Red Neuronal con tan solo una capa oculta.
Habiendo verificado que nuestro modelo entrenado funciona bastante bien con el set de validación, podemos ahora usarlo para realizar predicciones.
Para ello podemos tomar algunas imágenes del set de validación, y usar el método predict_classes para que el modelo prediga la categoría a la que pertenece:
Y_pred = modelo.predict_classes(X_test)
ids_imgs = np.random.randint(0,X_test.shape[0],9)
for i in range(len(ids_imgs)):
idx = ids_imgs[i]
img = X_test[idx,:].reshape(28,28)
cat_original = np.argmax(Y_test[idx,:])
cat_prediccion = Y_pred[idx]
plt.subplot(3,3,i+1)
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.title('"{}" clasificado como "{}"'.format(cat_original,cat_prediccion))
plt.suptitle('Ejemplos de clasificación en el set de validación')
plt.show()
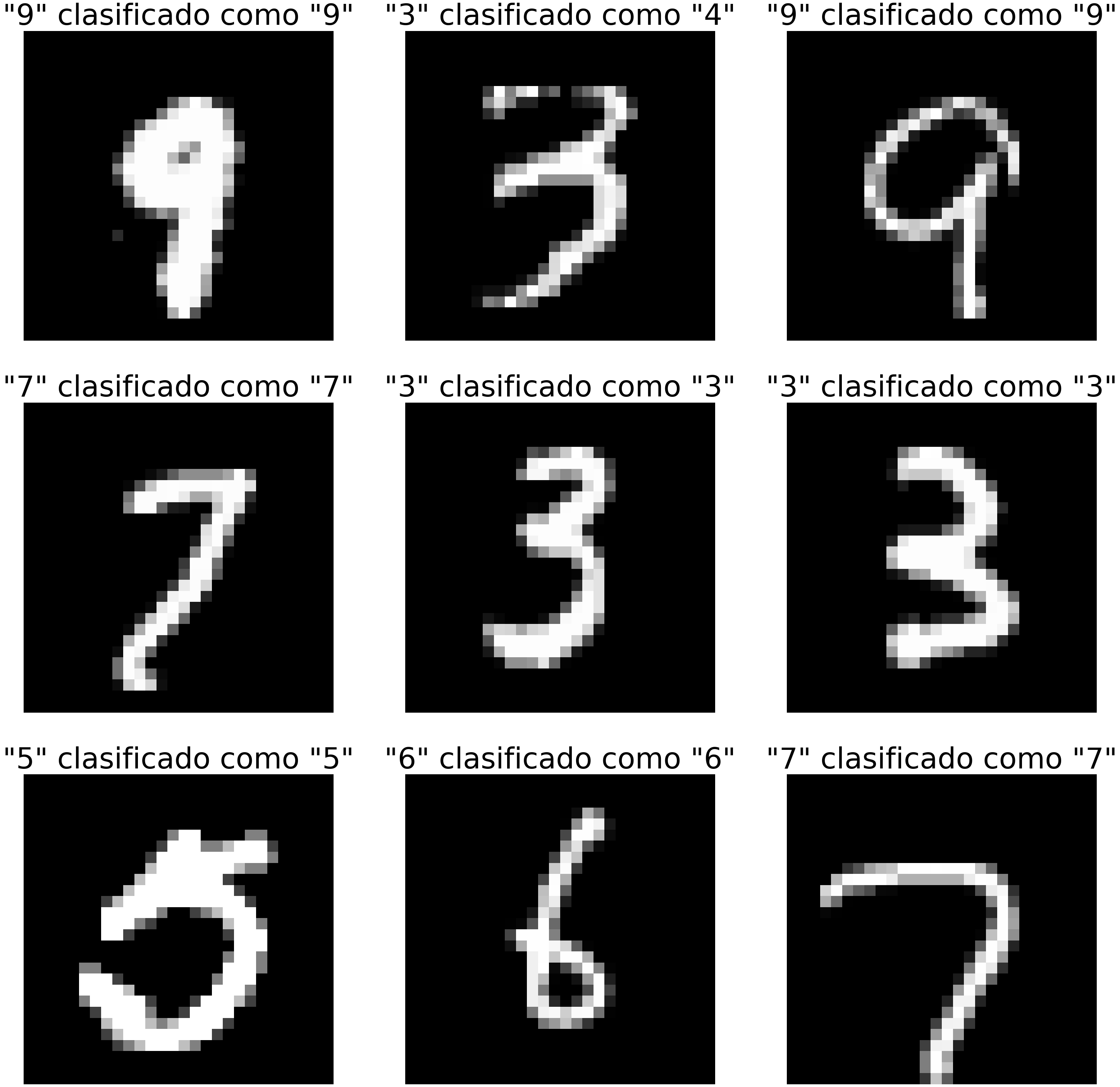
Vemos que este resultado coincide con la precisión encontrada durante la validación (e igual al 94.4%): la mayoría de las imágenes de prueba fue clasificada correctamente, exceptuando el dígito tres en la primera fila, el cual fue erróneamente clasificado como un 4.
Conclusión
Bien, en este tutorial vimos cómo clasificar imágenes de dígitos escritos a mano usando una Red Neuronal y la librería Keras. Vimos que a pesar de que estas redes no se especializan en el procesamiento de imágenes, en todo caso la precisión alcanzada con el set de validación es bastante alta e igual al 94.4%, lo cual quiere decir que prácticamente de cada 100 imágenes tan sólo 5 son clasificadas incorrectamente.
Si tienes alguna duda de este artículo o tienes alguna sugerencia no dudes en contactarme diligenciando el siguiente formulario:
Datos y código fuente
En este enlace de Github podrás descargar el código fuente de este tutorial.